您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
本篇內容主要講解“Java集合和數據結構排序的實例介紹”,感興趣的朋友不妨來看看。本文介紹的方法操作簡單快捷,實用性強。下面就讓小編來帶大家學習“Java集合和數據結構排序的實例介紹”吧!
概念
插入排序
直接插入排序
代碼實現
性能分析
希爾排序
代碼實現
性能分析
選擇排序
直接選擇排序
代碼實現
性能分析
堆排序
代碼實現
性能分析
交換排序
冒泡排序
代碼實現
性能分析
快速排序
代碼實現
性能分析
非遞歸實現快速排序
代碼實現
性能分析
歸并排序
歸并排序
代碼實現
性能分析
非遞歸實現歸并排序
代碼實現
性能分析
海量數據的排序問題
排序,就是使一串記錄,按照其中的某個或某些關鍵字的大小,遞增或遞減的排列起來的操作。
平時的上下文中,如果提到排序,通常指的是排升序(非降序)。
通常意義上的排序,都是指的原地排序(in place sort)。
穩定性: 兩個相等的數據,如果經過排序后,排序算法能保證其相對位置不發生變化,則我們稱該算法是具備穩定性的排序算法。
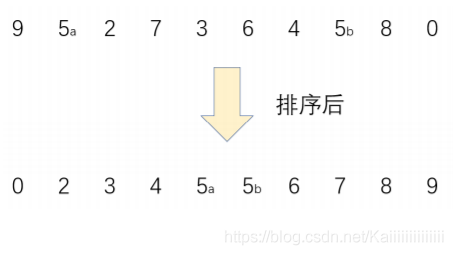

整個區間被分為
有序區間
無序區間
每次選擇無序區間的第一個元素,在有序區間內選擇合適的位置插入
邏輯代碼:
public class InsertSort {
public static void insertSort(int[] array) {
for (int i = 1; i < array.length; i++) {
int temp = array[i];
int j = i-1;
for (; j >= 0; j--) {
if (array[j] > temp) {
array[j+1] = array[j];
}else {
break;
}
}
array[j+1] = temp;
}
}
}調試代碼:
public class TestDemo {
public static void main(String[] args) {
int[] array = {10,3,2,7,19,78,65,127};
System.out.println("排序前:" + Arrays.toString(array));
InsertSort.insertSort(array);
System.out.println("排序后:" + Arrays.toString(array));
}
}該代碼的執行結果為:
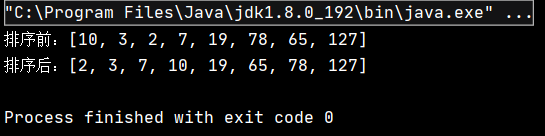
可見,實現了對原數組的升序排序。
時間復雜度:
最好情況:O(n)【數據有序】
平均情況:O(n2)
最壞情況:O(n2)【數據逆序】
空間復雜度:O(1)
穩定性:穩定
對于直接插入排序:越有序越快。另外,直接插入排序會用在一些排序的優化上。
希爾排序法又稱縮小增量法。希爾排序法的基本思想是:先選定一個整數,把待排序文件中所有記錄分成個組,所有距離為的記錄分在同一組內,并對每一組內的記錄進行排序。然后,取,重復上述分組和排序的工作。當到達=1時, 所有記錄在統一組內排好序。
希爾排序是對直接插入排序的優化。
當gap > 1時都是預排序,目的是讓數組更接近于有序。當gap == 1時,數組已經接近有序的了,這樣就會很快。這樣整體而言,可以達到優化的效果。我們實現后可以進行性能測試的對比。
邏輯代碼:
public class ShellSort {
public static void shell(int[] array,int gap) {
for (int i = gap; i < array.length; i = i + gap) {
int temp = array[i];
int j = i-gap;
for (; j >= 0; j = j-gap) {
if (array[j] > temp) {
array[j+gap] = array[j];
}else {
break;
}
}
array[j+gap] = temp;
}
}
public static void shellSort(int[] array) {
int[] drr = {5,3,1};//增量數組-->沒有明確的規定,但保證為素數的增量序列
for (int i = 0; i < drr.length; i++) {
shell(array,drr[i]);
}
}
}測試代碼:
public class TestDemo {
public static void main(String[] args) {
int[] array = {10,3,2,7,19,78,65,127};
System.out.println("排序前:" + Arrays.toString(array));
ShellSort.shellSort(array);
System.out.println("排序后:" + Arrays.toString(array));
}
}該代碼的執行結果為:
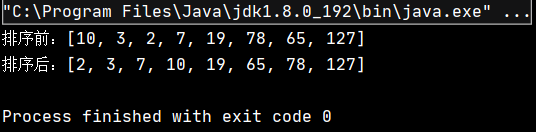
可見,實現了對原數組的升序排序。
時間復雜度:
最好情況:O(n)【數據有序】
平均情況:O(n1.3)
最壞情況: O(n2) 【比較難構造】
空間復雜度:O(1)
穩定性:不穩定
每一次從無序區間選出最大(或最小)的一個元素,存放在無序區間的最后(或最前),直到全部待排序的數據元素排完 。
邏輯代碼:
public class SelectSort {
public static void selectSort(int[] array) {
for (int i = 0; i < array.length-1; i++) {
for (int j = i+1; j < array.length; j++) {
if (array[i] > array[j]) {
int temp = array[j];
array[j] = array[i];
array[i] = temp;
}
}
}
}
}測試代碼:
public class TestDemo {
public static void main(String[] args) {
int[] array = {10,3,2,7,19,78,65,127};
System.out.println("排序前:" + Arrays.toString(array));
SelectSort.selectSort(array);
System.out.println("排序后:" + Arrays.toString(array));
}
}該代碼的執行結果為:
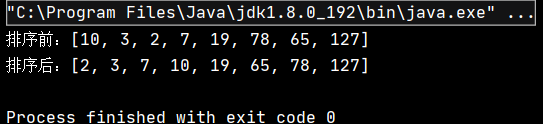
可見,實現了對原數組的升序排序。
時間復雜度 : 不管是最好情況還是最壞情況都是O(n2) 【數據不敏感】
空間復雜度: O(1)
穩定性:不穩定
基本原理也是選擇排序,只是不在使用遍歷的方式查找無序區間的最大的數,而是通過堆來選擇無序區間的最大的數。
注意:排升序要建大堆;排降序要建小堆。
邏輯代碼:
public class HeapSort {
public static void heapSort(int[] array) {
PriorityQueue<Integer> priorityQueue = new PriorityQueue<>(new Comparator<Integer>() {
@Override
public int compare(Integer o1, Integer o2) {
return o1-o2;
}
});
for (int i = 0; i < array.length; i++) {
priorityQueue.add(array[i]);
}
for (int i = 0; i < array.length; i++) {
array[i] = priorityQueue.poll();
}
}
}測試代碼:
public class TestDemo {
public static void main(String[] args) {
int[] array = {10,3,2,7,19,78,65,127};
System.out.println("排序前:" + Arrays.toString(array));
HeapSort.heapSort(array);
System.out.println("排序后:" + Arrays.toString(array));
}
}該代碼的執行結果為:
可見,實現了對原數組的升序排序。
時間復雜度:不管是最好的情況還是最壞的情況都是O(n * log(n)) 。
空間復雜度:O(1)。
穩定性:不穩定
在無序區間,通過相鄰數的比較,將最大的數冒泡到無序區間的最后,持續這個過程,直到數組整體有序。
邏輯代碼:
public class BubbleBort {
public static void bubbleBort(int[] array) {
for (int i = 0; i < array.length-1; i++) {
for (int j = 0; j < array.length-i-1; j++) {
if (array[j] > array[j+1]) {
int temp = array[j];
array[j] = array[j+1];
array[j+1] = temp;
}
}
}
}
}測試代碼:
public class TestDemo {
public static void main(String[] args) {
int[] array = {10,3,2,7,19,78,65,127};
System.out.println("排序前:" + Arrays.toString(array));
BubbleBort.bubbleBort(array);
System.out.println("排序后:" + Arrays.toString(array));
}
}該代碼的執行結果為:
可見,實現了對原數組的升序排序。
時間復雜度:
最好情況:O(n)【數據有序】
平均情況:O(n2)
最壞情況: O(n2) 【數據逆序】
空間復雜度:O(1)。
穩定性:穩定
從待排序區間選擇一個數,作為基準值(pivot);
Partition: 遍歷整個待排序區間,將比基準值小的(可以包含相等的)放到基準值的左邊,將比基準值大的(可以包含相等的)放到基準值的右邊;
采用分治思想,對左右兩個小區間按照同樣的方式處理,直到小區間的長度 = 1,代表已經有序,或者小區間的長度 = 0,代表沒有數據。
邏輯代碼:
public class QuickSort {
public static void quick(int[] array,int low,int high) {
if (low < high) {
int piv = piovt(array,low,high);//找基準
quick(array,low,piv-1);
quick(array,piv+1,high);
}
}
private static int piovt(int[] array,int start,int end) {
int temp = array[start];
while (start < end) {
while (start < end && array[end] >= temp) {
end--;
}
array[start] = array[end];
while (start < end && array[start] < temp) {
start++;
}
array[end] = array[start];
}
array[start] = temp;
return start;
}
public static void quickSort(int[] array) {
quick(array,0,array.length-1);
}
}測試代碼:
public class TestDemo {
public static void main(String[] args) {
int[] array = {10,3,2,7,19,78,65,127};
System.out.println("排序前:" + Arrays.toString(array));
QuickSort.quickSort(array);
System.out.println("排序后:" + Arrays.toString(array));
}
}該代碼的執行結果為:
可見,實現了對原數組的升序排序。
時間復雜度:
最好情況:O(n * log(n))
平均情況:O(n * log(n))
最壞情況: O(n2)
空間復雜度:
最好情況:O(log(n))
平均情況:O(log(n))
最壞情況:O(n)
穩定性:不穩定
邏輯代碼:
/**
* 非遞歸實現快速排序
*/
public class QuickSortNor {
public static void quickSortNor(int[] array) {
int low = 0;
int high = array.length - 1;
int piv = piovt(array, low, high);
Stack<Integer> stack = new Stack<>();
if (piv > low + 1) {
stack.push(low);
stack.push(piv - 1);
}
if (piv < high - 1) {
stack.push(piv + 1);
stack.push(high);
}
while (!stack.isEmpty()) {
high = stack.pop();
low = stack.pop();
piv = piovt(array, low, high);
if (piv > low + 1) {
stack.push(low);
stack.push(piv - 1);
}
if (piv < high - 1) {
stack.push(piv + 1);
stack.push(high);
}
}
}
private static int piovt(int[] array, int start, int end) {
int temp = array[start];
while (start < end) {
while (start < end && array[end] >= temp) {
end--;
}
array[start] = array[end];
while (start < end && array[start] < temp) {
start++;
}
array[end] = array[start];
}
array[start] = temp;
return start;
}
}測試代碼:
public class TestDemo {
public static void main(String[] args) {
int[] array = {10,3,2,7,19,78,65,127};
System.out.println("排序前:" + Arrays.toString(array));
QuickSortNor.quickSortNor(array);
System.out.println("排序后:" + Arrays.toString(array));
}
}該代碼的執行結果為:
可見,實現了對原數組的升序排序。
時間復雜度: O(n * log(n))
空間復雜度:
最好情況:O(log(n))
最壞情況:O(n)
穩定性:不穩定
歸并排序(MERGE-SORT)是建立在歸并操作上的一種有效的排序算法,該算法是采用分治法(Divide and Conquer)的一個非常典型的應用。將已有序的子序列合并,得到完全有序的序列;即先使每個子序列有序,再使子序列段間有序。若將兩個有序表合并成一個有序表,稱為二路歸并。
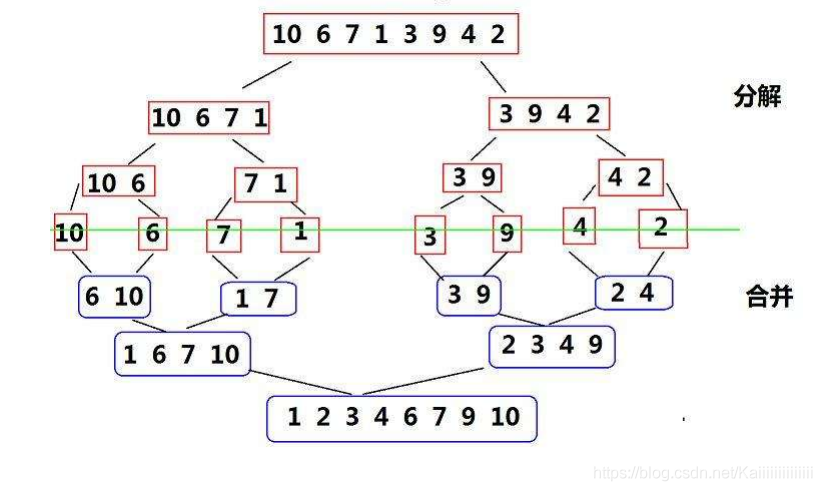
邏輯代碼:
public class MergeSort {
public static void merge(int[] array, int start, int mid, int end) {
int s1 = start;
int s2 = mid + 1;
int[] temp = new int[end - start + 1];
int k = 0;
while (s1 <= mid && s2 <= end) {
if (array[s1] <= array[s2]) {
temp[k++] = array[s1++];
} else {
temp[k++] = array[s2++];
}
}
while (s1 <= mid) {
temp[k++] = array[s1++];
}
while (s2 <= end) {
temp[k++] = array[s2++];
}
for (int i = 0; i < temp.length; i++) {
array[i + start] = temp[i];
}
}
public static void mergeSortInternal(int[] array, int low, int high) {
if (low >= high) return;
//先分解
int mid = (low + high) / 2;
mergeSortInternal(array, low, mid);
mergeSortInternal(array, mid + 1, high);
//再合并
merge(array, low, mid, high);
}
public static void mergeSort(int[] array) {
mergeSortInternal(array, 0, array.length - 1);
}
}測試代碼:
public class TestDemo {
public static void main(String[] args) {
int[] array = {10,3,2,7,19,78,65,127};
System.out.println("排序前:" + Arrays.toString(array));
MergeSort.mergeSort(array);
System.out.println("排序后:" + Arrays.toString(array));
}
}該代碼的執行結果為:
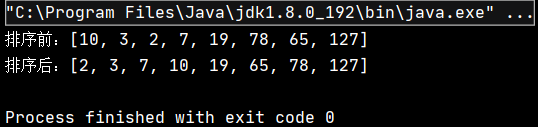
可見,實現了對原數組的升序排序。
時間復雜度: O(n * log(n))
空間復雜度:O(n)
穩定性:穩定
邏輯代碼:
/**
* 非遞歸實現歸并排序
*/
public class MergeSortNor {
public static void merge(int[] array, int gap) {
int s1 = 0;
int e1 = s1 + gap - 1;
int s2 = e1 + 1;
int e2 = s2 + gap - 1 < array.length ? s2 + gap - 1 : array.length - 1;
int[] temp = new int[array.length];
int k = 0;
while (s2 < array.length) {
while (s1 <= e1 && s2 <= e2) {
if (array[s1] <= array[s2]) {
temp[k++] = array[s1++];
} else {
temp[k++] = array[s2++];
}
}
while (s1 <= e1) {
temp[k++] = array[s1++];
}
while (s2 <= e2) {
temp[k++] = array[s2++];
}
s1 = e2+1;
e1 = s1+gap-1;
s2 = e1+1;
e2 = s2 + gap - 1 < array.length ? s2 + gap - 1 : array.length - 1;
}
while (s1 < array.length) {
temp[k++] = array[s1++];
}
for (int i = 0; i < temp.length; i++) {
array[i] = temp[i];
}
}
public static void mergeSortNor(int[] array) {
for (int i = 1; i < array.length; i *= 2) {
merge(array, i);
}
}
}測試代碼:
public class TestDemo {
public static void main(String[] args) {
int[] array = {10,3,2,7,19,78,65,127};
System.out.println("排序前:" + Arrays.toString(array));
MergeSortNor.mergeSortNor(array);
System.out.println("排序后:" + Arrays.toString(array));
}
}該代碼的執行結果為:
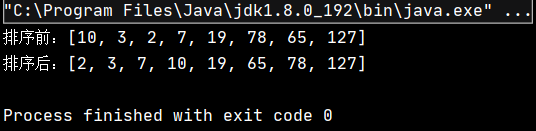
可見,實現了對原數組的升序排序。
時間復雜度: O(n * log(n))
空間復雜度:O(n)
穩定性:穩定
外部排序:排序過程需要在磁盤等外部存儲進行的排序
前提:內存只有 1G,需要排序的數據有 100G
因為內存中因為無法把所有數據全部放下,所以需要外部排序,而歸并排序是最常用的外部排序。
先把文件切分成 200 份,每個 512 M
分別對 512 M 排序,因為內存已經可以放的下,所以任意排序方式都可以
進行 200 路歸并,同時對 200 份有序文件做歸并過程,最終結果就有序了
排序總結
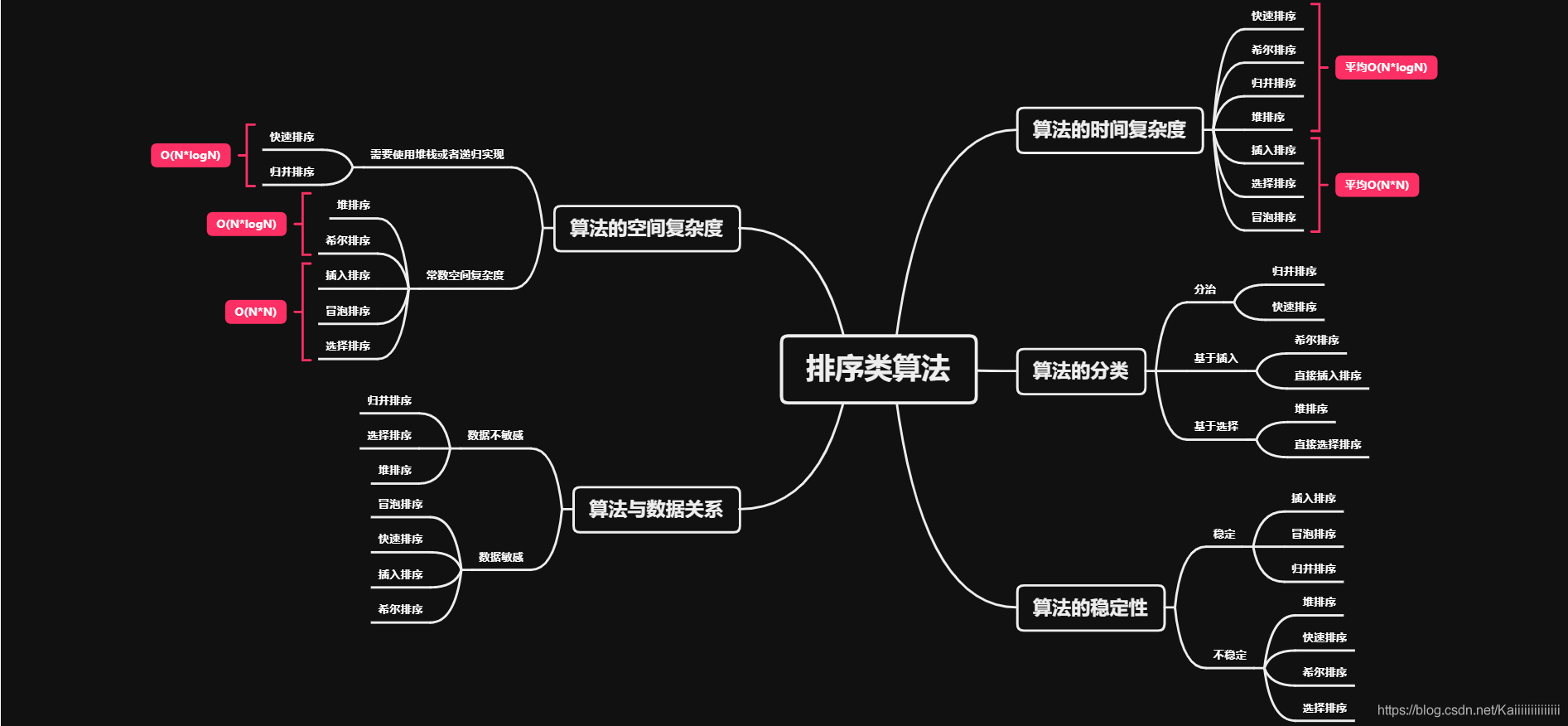
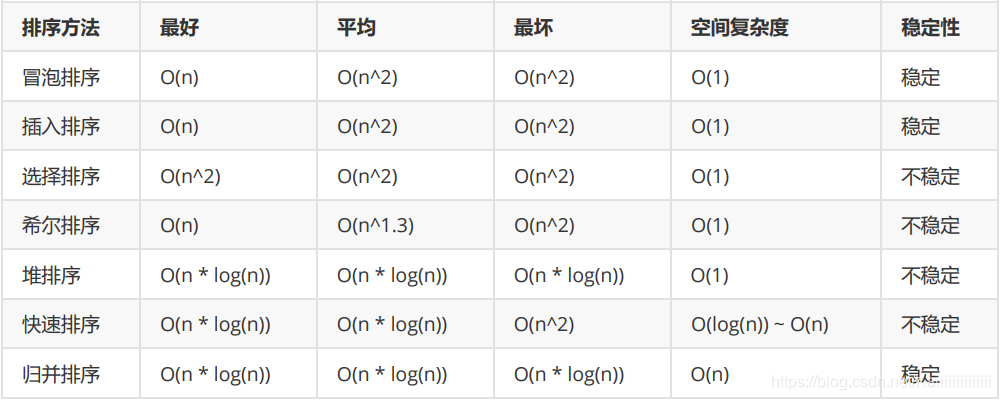
到此,相信大家對“Java集合和數據結構排序的實例介紹”有了更深的了解,不妨來實際操作一番吧!這里是億速云網站,更多相關內容可以進入相關頻道進行查詢,關注我們,繼續學習!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。