C++前綴和與差分算法的示例分析

這篇文章將為大家詳細講解有關C++前綴和與差分算法的示例分析，小編覺得挺實用的，因此分享給大家做個參考，希望大家閱讀完這篇文章后可以有所收獲。

1、前綴和

前綴和是指某序列的前n項和，可以把它理解為數學上的數列的前n項和，而差分可以看成前綴和的逆運算。合理的使用前綴和與差分，可以將某些復雜的問題簡單化。

2、前綴和算法有什么好處？

先來了解這樣一個問題：

輸入一個長度為n的整數序列。接下來再輸入m個詢問，每個詢問輸入一對l, r。對于每個詢問，輸出原序列中從第l個數到第r個數的和。

我們很容易想出暴力解法，遍歷區間求和。

代碼如下：

int n,m;
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++) scanf("%d",&a[i]);
while(m--)
{
    int l,r;
    int sum=0;
    scanf("%d%d",&l,&r);
    for(int i=l;i<=r;i++)
    { 
        sum+=a[i];
    }
    printf("%d\n",sum);
}

這樣的時間復雜度為O(n*m)，如果n和m的數據量稍微大一點就有可能超時，而我們如果使用前綴和的方法來做的話就能夠將時間復雜度降到O(n+m),大大提高了運算效率。

具體做法：

首先做一個預處理，定義一個sum[]數組，sum[i]代表a數組中前i個數的和。

求前綴和運算：

const int N=1e5+10;
int sum[N],a[N]; //sum[i]=a[1]+a[2]+a[3].....a[i];
for(int i=1;i<=n;i++)
{ 
    sum[i]=sum[i-1]+a[i];   
}

然后查詢操作：

 scanf("%d%d",&l,&r);
 printf("%d\n", sum[r]-sum[l-1]);

對于每次查詢，只需執行sum[r]-sum[l-1] ，時間復雜度為O(1)

原理

sum[r] =a[1]+a[2]+a[3]+a[l-1]+a[l]+a[l+1]......a[r];
sum[l-1]=a[1]+a[2]+a[3]+a[l-1];
sum[r]-sum[l-1]=a[l]+a[l+1]+......+a[r];

圖解

這樣，對于每個詢問，只需要執行 sum[r]-sum[l-1]。輸出原序列中從第l個數到第r個數的和的時間復雜度變成了O(1)。

我們把它叫做一維前綴和。

總結：

練習一道題目

輸入一個長度為n的整數序列。
接下來再輸入m個詢問，每個詢問輸入一對l, r。
對于每個詢問，輸出原序列中從第l個數到第r個數的和。

輸入格式

第一行包含兩個整數n和m。
第二行包含n個整數，表示整數數列。
接下來m行，每行包含兩個整數l和r，表示一個詢問的區間范圍。

輸出格式

共m行，每行輸出一個詢問的結果。

數據范圍

1≤l≤r≤n,
1≤n,m≤100000,
?1000≤數列中元素的值≤1000

輸入樣例：

5 3
2 1 3 6 4
1 2
1 3
2 4

輸出樣例：

3
6
10

代碼：

#include <iostream>
using namespace std;
const int N = 100010;
int n, m;
int a[N], s[N];
int main()
{
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i ++ ) scanf("%d", &a[i]);
    for (int i = 1; i <= n; i ++ ) s[i] = s[i - 1] + a[i]; // 前綴和的初始化
    while (m -- )
    {
        int l, r;
        scanf("%d%d", &l, &r);
        printf("%d\n", s[r] - s[l - 1]); // 區間和的計算
    }
    return 0;
}

3、二維前綴和

如果數組變成了二維數組怎么辦呢？

先給出問題：

輸入一個n行m列的整數矩陣，再輸入q個詢問，每個詢問包含四個整數x1, y1, x2, y2，表示一個子矩陣的左上角坐標和右下角坐標。對于每個詢問輸出子矩陣中所有數的和。

同一維前綴和一樣，我們先來定義一個二維數組s[][], s[i][j]表示二維數組中，左上角(1,1)到右下角( i,j )所包圍的矩陣元素的和。接下來推導二維前綴和的公式。

先看一張圖：

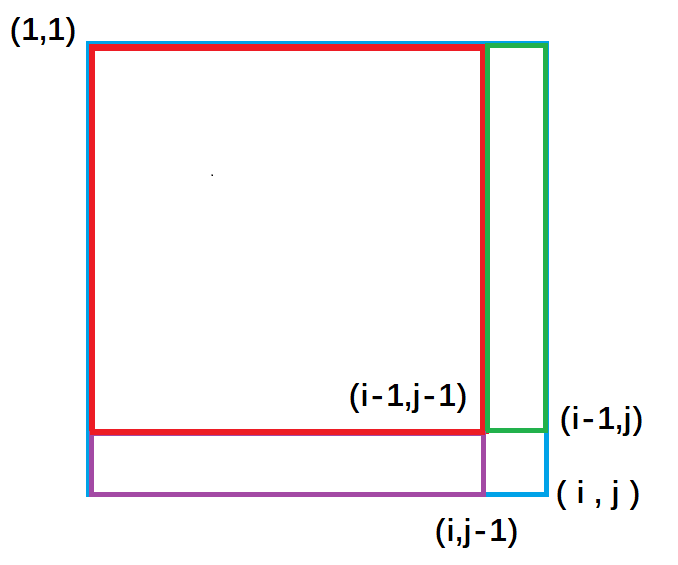
紫色面積是指(1,1)左上角到(i,j-1)右下角的矩形面積, 綠色面積是指(1,1)左上角到(i-1, j )右下角的矩形面積。每一個顏色的矩形面積都代表了它所包圍元素的和。

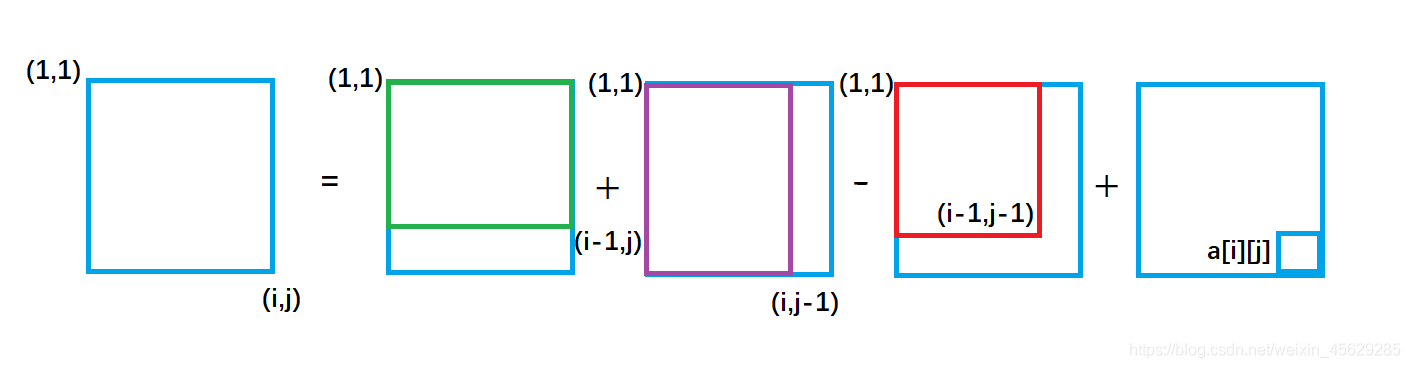
從圖中我們很容易看出，整個外圍藍色矩形面積s[i][j] = 綠色面積s[i-1][j] + 紫色面積s[i][j-1] - 重復加的紅色的面積s[i-1][j-1]+小方塊的面積a[i][j];

因此得出二維前綴和預處理公式

s[i] [j] = s[i-1][j] + s[i][j-1 ] + a[i] [j] - s[i-1][ j-1]

接下來回歸問題去求以(x1,y1)為左上角和以(x2,y2)為右下角的矩陣的元素的和。

如圖：

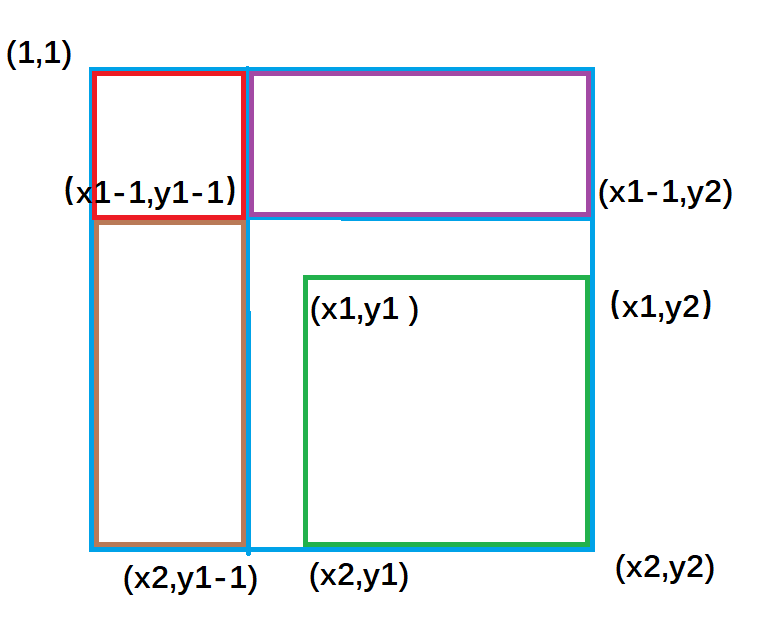
紫色面積是指 ( 1,1 )左上角到(x1-1,y2)右下角的矩形面積 ，黃色面積是指(1,1)左上角到(x2,y1-1)右下角的矩形面積；

不難推出：

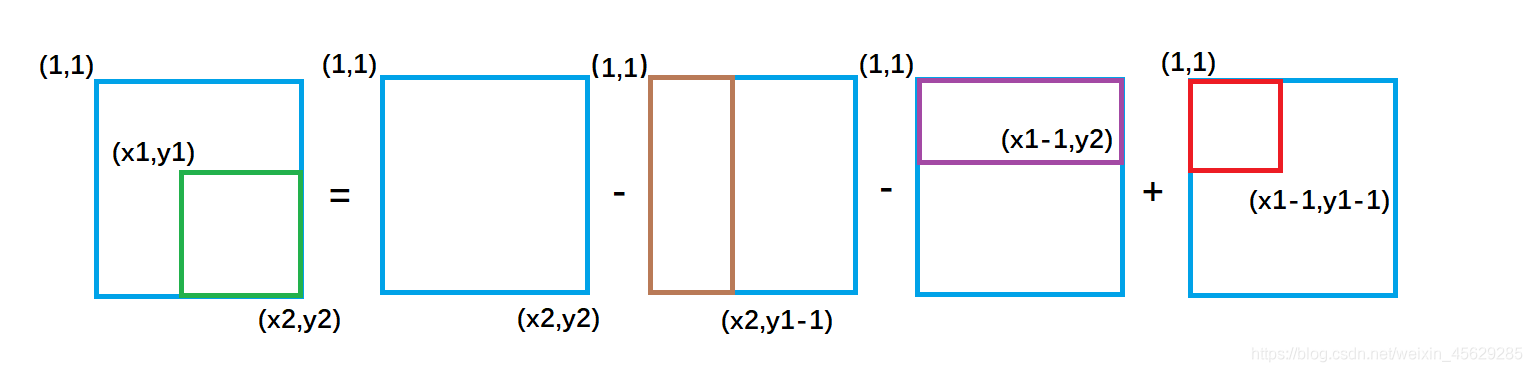
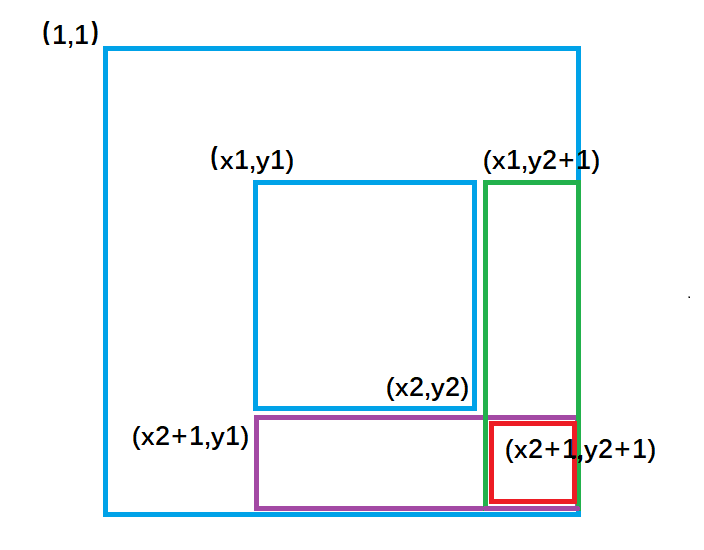
綠色矩形的面積 = 整個外圍面積s[x2, y2] - 黃色面積s[x2, y1 - 1] - 紫色面積s[x1 - 1, y2] + 重復減去的紅色面積 s[x1 - 1, y1 - 1]

因此二維前綴和的結論為：

以(x1, y1)為左上角，(x2, y2)為右下角的子矩陣的和為：

s[x2, y2] - s[x1 - 1, y2] - s[x2, y1 - 1] + s[x1 - 1, y1 - 1]

總結：

練習一道完整題目：
輸入一個n行m列的整數矩陣，再輸入q個詢問，每個詢問包含四個整數x1, y1, x2, y2，表示一個子矩陣的左上角坐標和右下角坐標。

對于每個詢問輸出子矩陣中所有數的和。

輸入格式

第一行包含三個整數n，m，q。
接下來n行，每行包含m個整數，表示整數矩陣。
接下來q行，每行包含四個整數x1, y1, x2, y2，表示一組詢問。

輸出格式

共q行，每行輸出一個詢問的結果。

數據范圍

1≤n,m≤1000,
1≤q≤200000,
1≤x1≤x2≤n,
1≤y1≤y2≤m,
?1000≤矩陣內元素的值≤1000

輸入樣例：

3 4 3
1 7 2 4
3 6 2 8
2 1 2 3
1 1 2 2
2 1 3 4
1 3 3 4

輸出樣例：

17
27
21

代碼：

#include<iostream>
#include<cstdio>
using namespace std;
const int N=1010;
int a[N][N],s[N][N];
int main()
{
    int n,m,q;
    scanf("%d%d%d",&n,&m,&q);
    for(int i=1;i<=n;i++)
      for(int j=1;j<=m;j++)
       scanf("%d",&a[i][j]);
    for(int i=1;i<=n;i++)
      for(int j=1;j<=m;j++)
        s[i][j]=s[i-1][j]+s[i][j-1]+a[i][j]-s[i-1][j-1];
    while(q--)
    {
        int x1,y1,x2,y2;
        scanf("%d%d%d%d",&x1,&y1,&x2,&y2);
        printf("%d\n",s[x2][y2]-s[x2][y1-1]-s[x1-1][y2]+s[x1-1][y1-1]);
    }
    return 0;
}

4、差分

5、一維差分

類似于數學中的求導和積分，差分可以看成前綴和的逆運算。

差分數組：

首先給定一個原數組a：a[1], a[2], a[3],,,,,, a[n];

然后我們構造一個數組b ： b[1] ,b[2] , b[3],,,,,, b[i];

使得 a[i] = b[1] + b[2 ]+ b[3] +,,,,,, + b[i]

也就是說，a數組是b數組的前綴和數組，反過來我們把b數組叫做a數組的差分數組。換句話說，每一個a[i]都是b數組中從頭開始的一段區間和。

考慮如何構造差分b數組？

最為直接的方法

如下：

a[0 ]= 0;

b[1] = a[1] - a[0];

b[2] = a[2] - a[1];

b[3] =a [3] - a[2];

........

b[n] = a[n] - a[n-1];

圖示:

我們只要有b數組，通過前綴和運算，就可以在O(n) 的時間內得到a數組 。

知道了差分數組有什么用呢？ 別著急，慢慢往下看。

話說有這么一個問題：

給定區間[l ,r ]，讓我們把a數組中的[ l, r]區間中的每一個數都加上c,

即 a[l] + c , a[l+1] + c , a[l+2] + c ,,,,,, a[r] + c;

暴力做法是for循環l到r區間，時間復雜度O(n)，如果我們需要對原數組執行m次這樣的操作，時間復雜度就會變成O(n*m)。有沒有更高效的做法嗎? 考慮差分做法，(差分數組派上用場了)。

始終要記得，a數組是b數組的前綴和數組，比如對b數組的b[i]的修改，會影響到a數組中從a[i]及往后的每一個數。

首先讓差分b數組中的 b[l] + c ,通過前綴和運算，a數組變成 a[l] + c ,a[l+1] + c,,,,,, a[n] + c;

然后我們打個補丁，b[r+1] - c, 通過前綴和運算，a數組變成 a[r+1] - c,a[r+2] - c,,,,,,,a[n] - c;

為啥還要打個補丁？

我們畫個圖理解一下這個公式的由來:

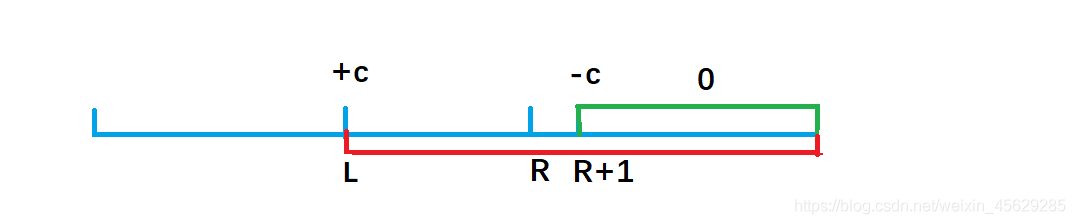
b[l] + c，效果使得a數組中 a[l]及以后的數都加上了c(紅色部分)，但我們只要求l到r區間加上c, 因此還需要執行 b[r+1] - c,讓a數組中a[r+1]及往后的區間再減去c(綠色部分)，這樣對于a[r] 以后區間的數相當于沒有發生改變。

因此我們得出一維差分結論：給a數組中的[ l, r]區間中的每一個數都加上c,只需對差分數組b做 b[l] + = c, b[r+1] - = c。時間復雜度為O(1), 大大提高了效率。

總結：

題目練習： AcWing 797. 差分

輸入一個長度為n的整數序列。
接下來輸入m個操作，每個操作包含三個整數l, r, c，表示將序列中[l, r]之間的每個數加上c。
請你輸出進行完所有操作后的序列。

輸入格式

第一行包含兩個整數n和m。
第二行包含n個整數，表示整數序列。
接下來m行，每行包含三個整數l，r，c，表示一個操作。

輸出格式

共一行，包含n個整數，表示最終序列。

數據范圍

1≤n,m≤100000,
1≤l≤r≤n,
?1000≤c≤1000,
?1000≤整數序列中元素的值≤1000

輸入樣例：

6 3
1 2 2 1 2 1
1 3 1
3 5 1
1 6 1

輸出樣例：

3 4 5 3 4 2
AC代碼

//差分 時間復雜度 o(m)
#include<iostream>
using namespace std;
const int N=1e5+10;
int a[N],b[N]; 
int main()
{
    int n,m;
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++) 
    {
        scanf("%d",&a[i]);
        b[i]=a[i]-a[i-1];      //構建差分數組
    }
    int l,r,c;
    while(m--)
    {
        scanf("%d%d%d",&l,&r,&c);
        b[l]+=c;     //表示將序列中[l, r]之間的每個數加上c
        b[r+1]-=c;
    }
    for(int i=1;i<=n;i++) 
    {
        b[i]+=b[i-1];  //求前綴和運算
        printf("%d ",b[i]);
    }
    return 0;
}

6、二維差分

如果擴展到二維，我們需要讓二維數組被選中的子矩陣中的每個元素的值加上c,是否也可以達到O(1)的時間復雜度。答案是可以的，考慮二維差分。

a[][]數組是b[][]數組的前綴和數組，那么b[][]是a[][]的差分數組

原數組： a[i][j]

我們去構造差分數組： b[i][j]

使得a數組中a[i][j]是b數組左上角(1,1)到右下角(i,j)所包圍矩形元素的和。

如何構造b數組呢？

其實關于差分數組，我們并不用考慮其構造方法，因為我們使用差分操作在對原數組進行修改的過程中，實際上就可以構造出差分數組。

同一維差分，我們構造二維差分數組目的是為了 讓原二維數組a中所選中子矩陣中的每一個元素加上c的操作，可以由O(n*n)的時間復雜度優化成O(1)

已知原數組a中被選中的子矩陣為 以(x1,y1)為左上角，以(x2,y2)為右上角所圍成的矩形區域;

始終要記得，a數組是b數組的前綴和數組，比如對b數組的b[i][j]的修改，會影響到a數組中從a[i][j]及往后的每一個數。

假定我們已經構造好了b數組，類比一維差分，我們執行以下操作
來使被選中的子矩陣中的每個元素的值加上c

b[x1][y1] + = c;

b[x1,][y2+1] - = c;

b[x2+1][y1] - = c;

b[x2+1][y2+1] + = c;

每次對b數組執行以上操作，等價于：

for(int i=x1;i<=x2;i++)
  for(int j=y1;j<=y2;j++)
    a[i][j]+=c;

我們畫個圖去理解一下這個過程：

b[x1][ y1 ] +=c ; 對應圖1 ,讓整個a數組中藍色矩形面積的元素都加上了c。
b[x1,][y2+1]-=c ; 對應圖2 ,讓整個a數組中綠色矩形面積的元素再減去c，使其內元素不發生改變。
b[x2+1][y1]- =c ; 對應圖3 ,讓整個a數組中紫色矩形面積的元素再減去c，使其內元素不發生改變。
b[x2+1][y2+1]+=c; 對應圖4,讓整個a數組中紅色矩形面積的元素再加上c，紅色內的相當于被減了兩次，再加上一次c，才能使其恢復。

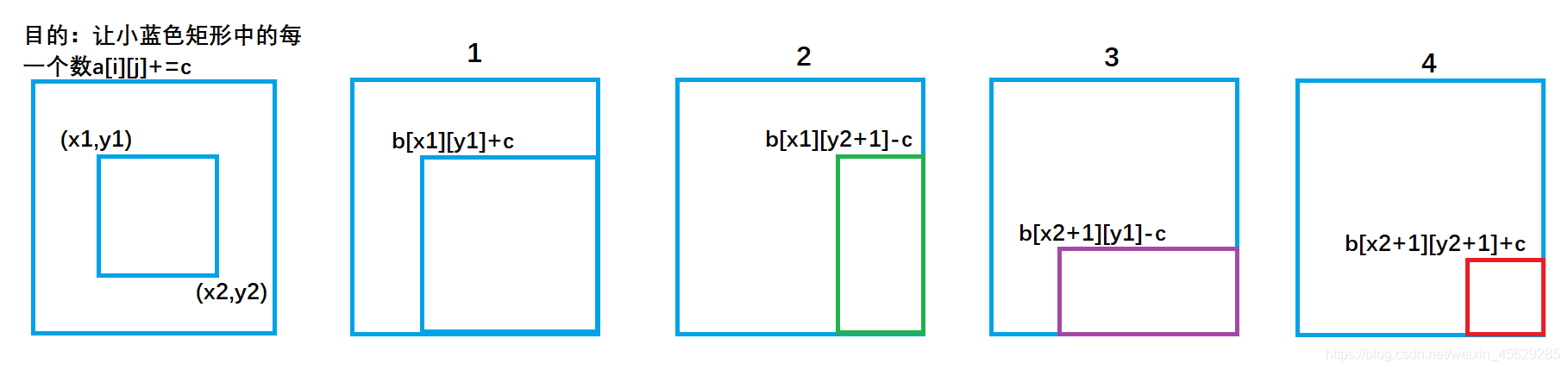
我們將上述操作封裝成一個插入函數:

void insert(int x1,int y1,int x2,int y2,int c)
{     //對b數組執行插入操作，等價于對a數組中的(x1,y1)到(x2,y2)之間的元素都加上了c
    b[x1][y1]+=c;
    b[x2+1][y1]-=c;
    b[x1][y2+1]-=c;
    b[x2+1][y2+1]+=c;
}

我們可以先假想a數組為空，那么b數組一開始也為空，但是實際上a數組并不為空，因此我們每次讓以(i,j)為左上角到以(i,j)為右上角面積內元素(其實就是一個小方格的面積)去插入 c=a[i][j]，等價于原數組a中(i,j) 到(i,j)范圍內 加上了 a[i][j] ,因此執行n*m次插入操作，就成功構建了差分b數組.

這叫做曲線救國。

代碼如下：

  for(int i=1;i<=n;i++)
  {
      for(int j=1;j<=m;j++)
      {
          insert(i,j,i,j,a[i][j]);    //構建差分數組
      }
  }

當然關于二維差分操作也有直接的構造方法，公式如下：

b[i][j]=a[i][j]?a[i?1][j]?a[i][j?1]+a[i?1][j?1]

二維差分數組的構造同一維差分思維相同，因次在這里就不再展開敘述了。

總結：

題目練習： AcWing 798. 差分矩陣

輸入一個n行m列的整數矩陣，再輸入q個操作，每個操作包含五個整數x1, y1, x2, y2, c，其中(x1, y1)和(x2, y2)表示一個子矩陣的左上角坐標和右下角坐標。
每個操作都要將選中的子矩陣中的每個元素的值加上c。
請你將進行完所有操作后的矩陣輸出。

輸入格式

第一行包含整數n,m,q。
接下來n行，每行包含m個整數，表示整數矩陣。
接下來q行，每行包含5個整數x1, y1, x2, y2, c，表示一個操作。

輸出格式

共 n 行，每行 m 個整數，表示所有操作進行完畢后的最終矩陣。
數據范圍

1≤n,m≤1000,
1≤q≤100000,
1≤x1≤x2≤n,
1≤y1≤y2≤m,
?1000≤c≤1000,
?1000≤矩陣內元素的值≤1000

輸入樣例：

3 4 3
1 2 2 1
3 2 2 1
1 1 1 1
1 1 2 2 1
1 3 2 3 2
3 1 3 4 1

輸出樣例：

2 3 4 1
4 3 4 1
2 2 2 2

AC代碼：

include<iostream>
#include<cstdio>
using namespace std;
const int N=1e3+10;
int a[N][N],b[N][N];
void insert(int x1,int y1,int x2,int y2,int c)
{
    b[x1][y1]+=c;
    b[x2+1][y1]-=c;
    b[x1][y2+1]-=c;
    b[x2+1][y2+1]+=c;
}
int main()
{
  int n,m,q;
  cin>>n>>m>>q;  
  for(int i=1;i<=n;i++)
   for(int j=1;j<=m;j++)
    cin>>a[i][j];
  for(int i=1;i<=n;i++)
  {
      for(int j=1;j<=m;j++)
      {
          insert(i,j,i,j,a[i][j]);    //構建差分數組
      }
  }
  while(q--)
  {
      int x1,y1,x2,y2,c;
      cin>>x1>>y1>>x2>>y2>>c;
      insert(x1,y1,x2,y2,c);
  }
  for(int i=1;i<=n;i++)
  {
      for(int j=1;j<=m;j++)
      {
          b[i][j]+=b[i-1][j]+b[i][j-1]-b[i-1][j-1];
      }
  }
  for(int i=1;i<=n;i++)
  {
      for(int j=1;j<=m;j++)
      {
          printf("%d ",b[i][j]);
      }
      printf("\n");
  }
  return 0;
}

關于“C++前綴和與差分算法的示例分析”這篇文章就分享到這里了，希望以上內容可以對大家有一定的幫助，使各位可以學到更多知識，如果覺得文章不錯，請把它分享出去讓更多的人看到。