C++中最短路徑之弗洛伊德算法的示例分析

這篇文章將為大家詳細講解有關C++中最短路徑之弗洛伊德算法的示例分析，小編覺得挺實用的，因此分享給大家做個參考，希望大家閱讀完這篇文章后可以有所收獲。

現在我們有這么一張圖：

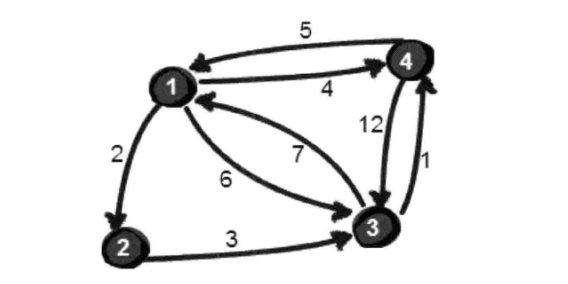
我們要做的是求出從某一點到達任意一點的最短距離，我們先用鄰接矩陣來建圖，map[i][j]表示從i點到j點的距離，把自己到自己設為0，把自己到不了的邊初始化為無窮大，代碼為：

//初始化
    for(int i=1; i<=n; i++)
        for(int j=1; j<=n; j++)
            if(i==j)
                map[i][j]=0;
            else
                map[i][j]=inf;
    //讀入邊
    for(int i=1; i<=m; i++)
    {
        scanf("%d%d%d",&t1,&t2,&t3);
        map[t1][t2]=t3;
    }

最后，建好的圖可以用表格來表示：

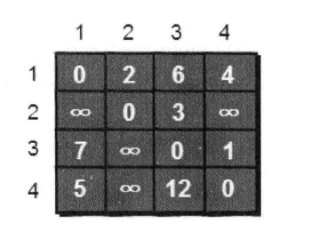
現在，我們來思考，假設我們來找一個中轉的點，看他們的路程會不會改變，我們先以1號頂點作為中轉點最為例子，制圖：

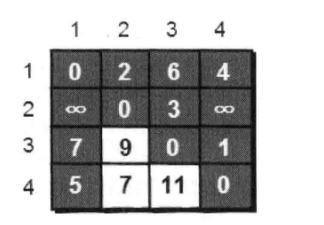
我們發現，圖有了變化，我們怎么判斷以1號頂點作為中轉點圖的路程是不是更短呢，我們只需要判斷map[i][1]+map[1][j]的路程是不是比map[i][j]的路程更短，就可以判斷，

代碼為：

for(int i=1; i<=n; i++)
    for(int j=1; j<=n; j++)
        if(map[i][1]+map[1][j]<map[i][j])
            map[i][j]=map[i][1]+map[1][j];

現在該怎么辦呢，我們接著以2號頂點作為中轉點，很簡單代碼修改一句就就可以：

for(int i=1; i<=n; i++)
    for(int j=1; j<=n; j++)
        if(map[i][2]+map[2][j]<map[i][j])
            map[i][j]=map[i][2]+map[2][j];

現在我們是不是發現了一個規律，只要不斷的遍歷每一個點，并且以每一個點作為中轉點看看它的值會不會改變，就可以得到從一個點到任意一個點的最短路徑，也就是多源最短路，這就是弗洛伊德算法，代碼為：

for(int k=1; k<=n; k++)
    for(int i=1; i<=n; i++)
        for(int j=1; j<=n; j++)
            if(map[i][k]+map[k][j]<map[i][j])
                map[i][j]=map[i][k]+map[k][j];

這樣就可以遍歷每個頂點，找出所有的最短路，算法的復雜度為O(n^3).

對于我一開始提出的問題，完整的代碼為：

#include <stdio.h>
#include <string.h>
#include <string>
#include <iostream>
#include <stack>
#include <queue>
#include <vector>
#include <algorithm>
#define mem(a,b) memset(a,b,sizeof(a))
using namespace std;
const int inf=1<<29;
int main()
{
    int map[10][10],n,m,t1,t2,t3;
    scanf("%d%d",&n,&m);//n表示頂點個數，m表示邊的條數
    //初始化
    for(int i=1; i<=n; i++)
        for(int j=1; j<=n; j++)
            if(i==j)
                map[i][j]=0;
            else
                map[i][j]=inf;
    //讀入邊
    for(int i=1; i<=m; i++)
    {
        scanf("%d%d%d",&t1,&t2,&t3);
        map[t1][t2]=t3;
    }
    //弗洛伊德(Floyd)核心語句
    for(int k=1; k<=n; k++)
        for(int i=1; i<=n; i++)
            for(int j=1; j<=n; j++)
                if(map[i][k]+map[k][j]<map[i][j])
                    map[i][j]=map[i][k]+map[k][j];
    for(int i=1; i<=n; i++)
    {
        for(int j=1; j<=n; j++)
            printf("%10d",map[i][j]);
        printf("\n");
    }
    return 0;
}

給出樣例：

輸入：

4 8
1 2 2
1 3 6
1 4 4
2 3 3
3 1 7
3 4 1
4 1 5
4 3 12

輸出：

 0         2         5         4
         9         0         3         4
         6         8         0         1
         5         7        10         0

輸出的就是我建圖的時候用的表格，可以表示任意一點到任意一點的最短距離。

關于“C++中最短路徑之弗洛伊德算法的示例分析”這篇文章就分享到這里了，希望以上內容可以對大家有一定的幫助，使各位可以學到更多知識，如果覺得文章不錯，請把它分享出去讓更多的人看到。