使用R語言與多元線性回歸分析計算的示例

這篇文章主要為大家展示了“使用R語言與多元線性回歸分析計算的示例”，內容簡而易懂，條理清晰，希望能夠幫助大家解決疑惑，下面讓小編帶領大家一起研究并學習一下“使用R語言與多元線性回歸分析計算的示例”這篇文章吧。

計算實例

例 6.9 某大型牙膏制造企業為了更好地拓展產品市場，有效地管理庫存，公司董事會要求銷售部門根據市場調查，找出公司生產的牙膏銷售量與銷售價格，廣告投入等之間的關系，從而預測出在不同價格和廣告費用下銷售量。為此，銷售部門的研究人員收集了過去30個銷售周期（每個銷售周期為4周）公司生產的牙膏的銷售量、銷售價格、投入的廣告費用，以及周期其他廠家生產同類牙膏的市場平均銷售價格，如表6.4所示。

試根據這些數據建立一個數學模型，分析牙膏銷售量與其他因素的關系，為制訂價格策略和廣告投入策略提供數量依據。

分析

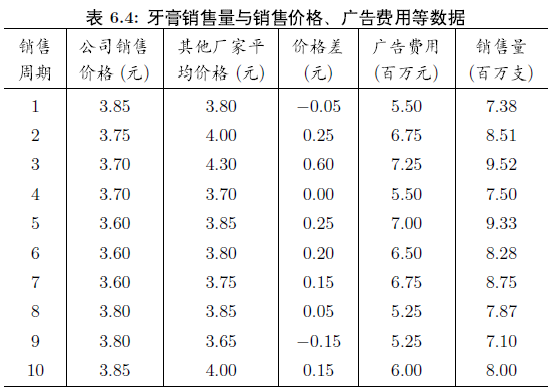
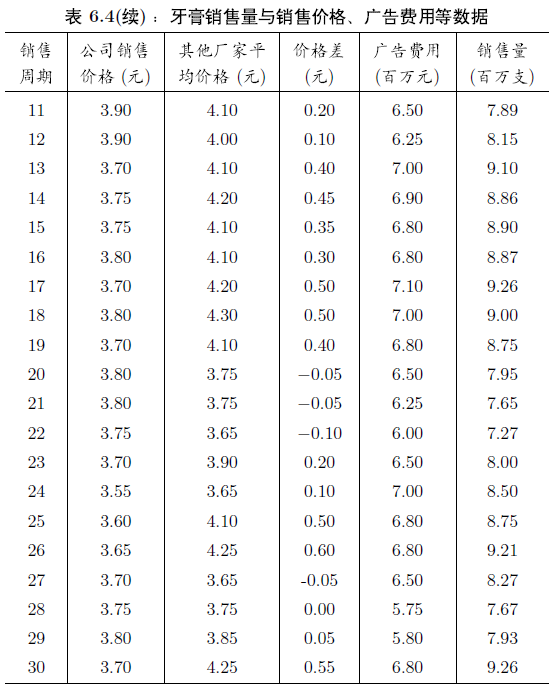
由于牙膏是生活的必需品，對于大多數顧客來說，在購買同類牙膏時，更多的會關心不同品牌之間的價格差，而不是它們的價格本身。因此，在研究各個因素對銷售量的影響時，用價格差代替公司銷售價格和其他廠家平均價格更為合適。

模型的建立與求解

記牙膏銷售量為Y，價格差為X1，公司的廣告費為X2，假設基本模型為線性模型:

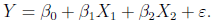
輸入數據，調用R軟件中的lm（）函數求解，并用summary（）顯示計算結果（程序名：exam0609.R）

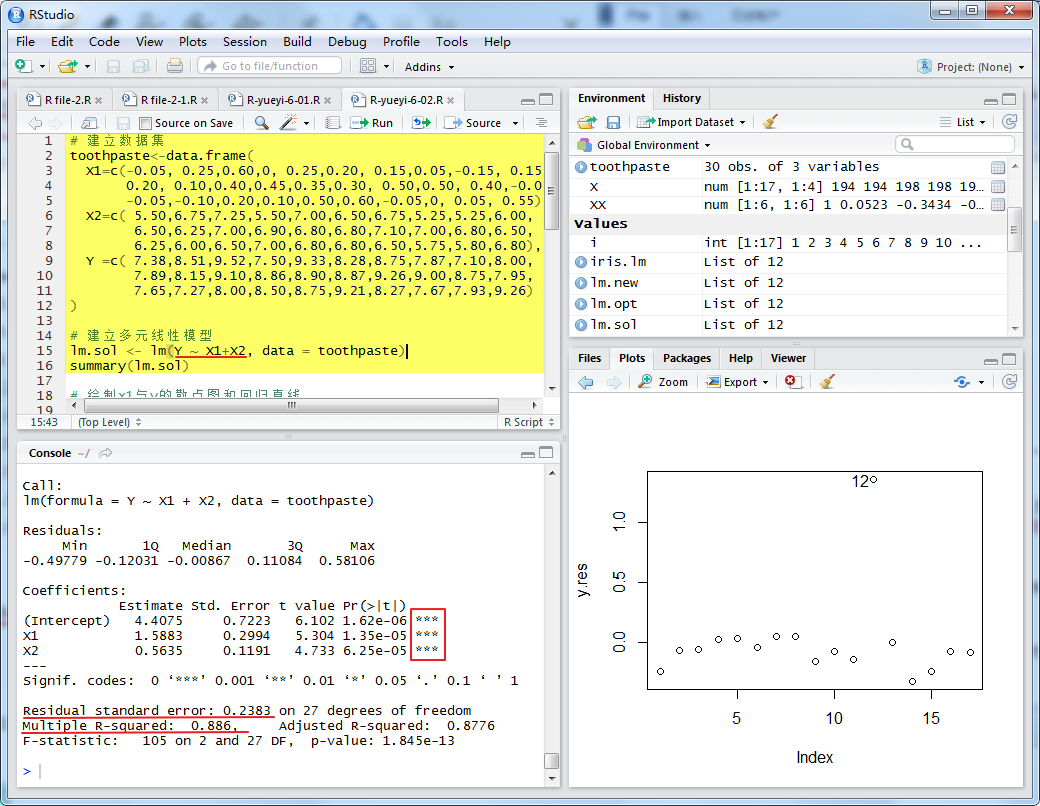
計算結果通過線性回歸系數檢驗和回歸方程檢驗，由此得到銷售量與價格差與廣告費之間的關系為：

模型的進一步分析

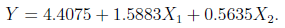
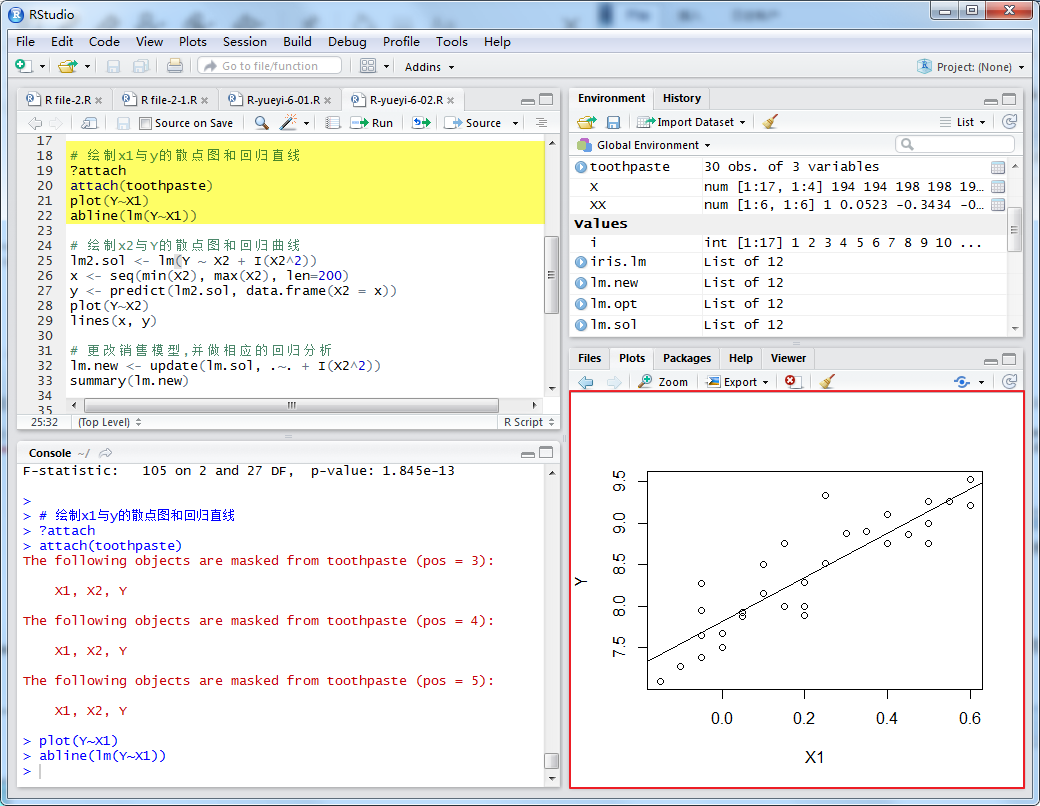
為進一步分析回歸模型，我們畫出y與x1和y與x2散點圖。從散點圖上可以看出，對于y與x1，用直線擬合較好。而對于y與x2，則用二次曲線擬合較好，如下圖：

繪制x1與y的散點圖和回歸直線

繪制x2與y的散點圖和回歸曲線

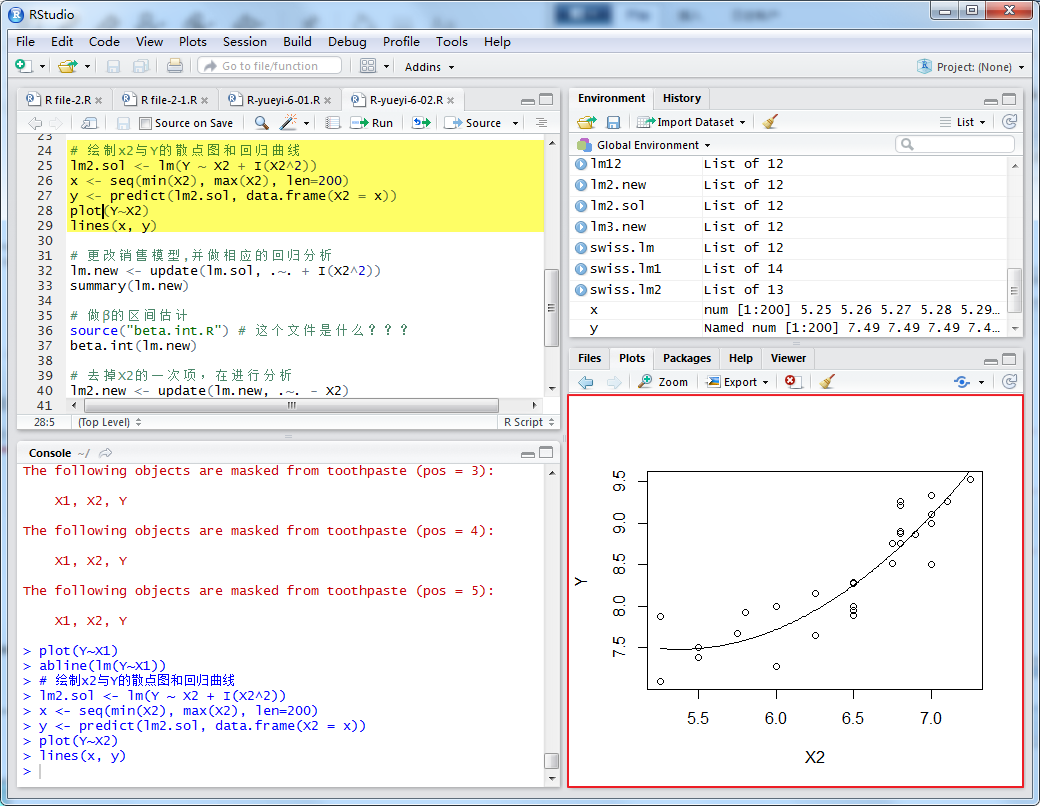
其中 I(X2^2)，表示模型中X2的平方項，及X22，從上圖中，將銷售量模型改為：

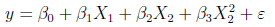
似乎更合理，我們做相應的回歸分析：

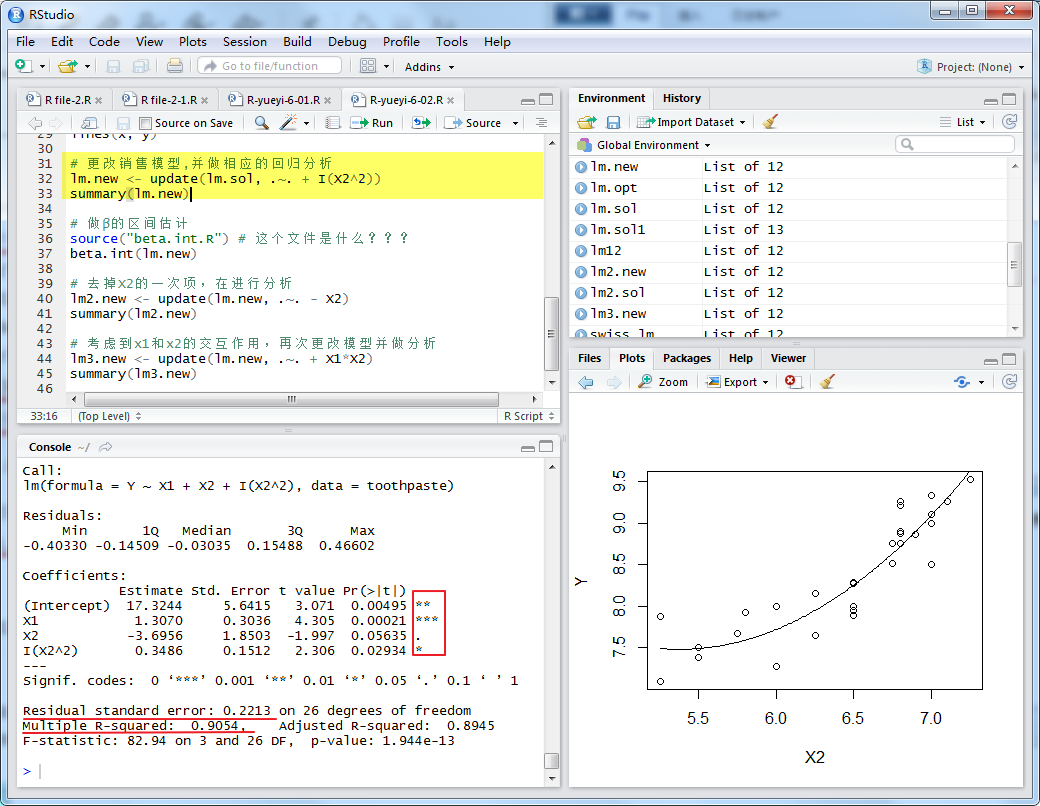
此時，我們發現，模型殘差的標準差Residual standard error有所下降，相關系數的平方Multiple R-squared有所上升，這說明模型修正的是合理的。但同時也出現了一個問題，就是對于β2的P-值>0.05。為進一步分析，做β的區間估計。

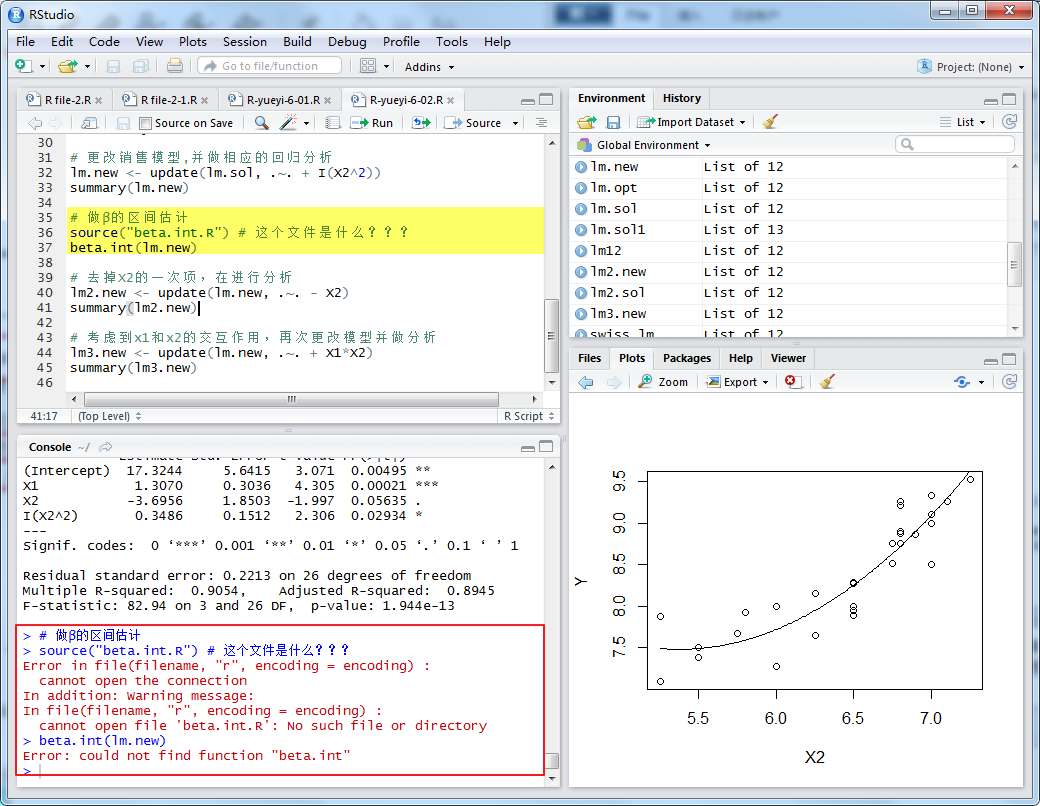
如上錯誤出現？？？？！！！！直接引用結果如下：

β2的區間估計為[ –7.49886317, 0.1076898 ]，它包含了0，也就是說，β2的值可能為0. 因此，去掉X2的一次項，在進行分析：

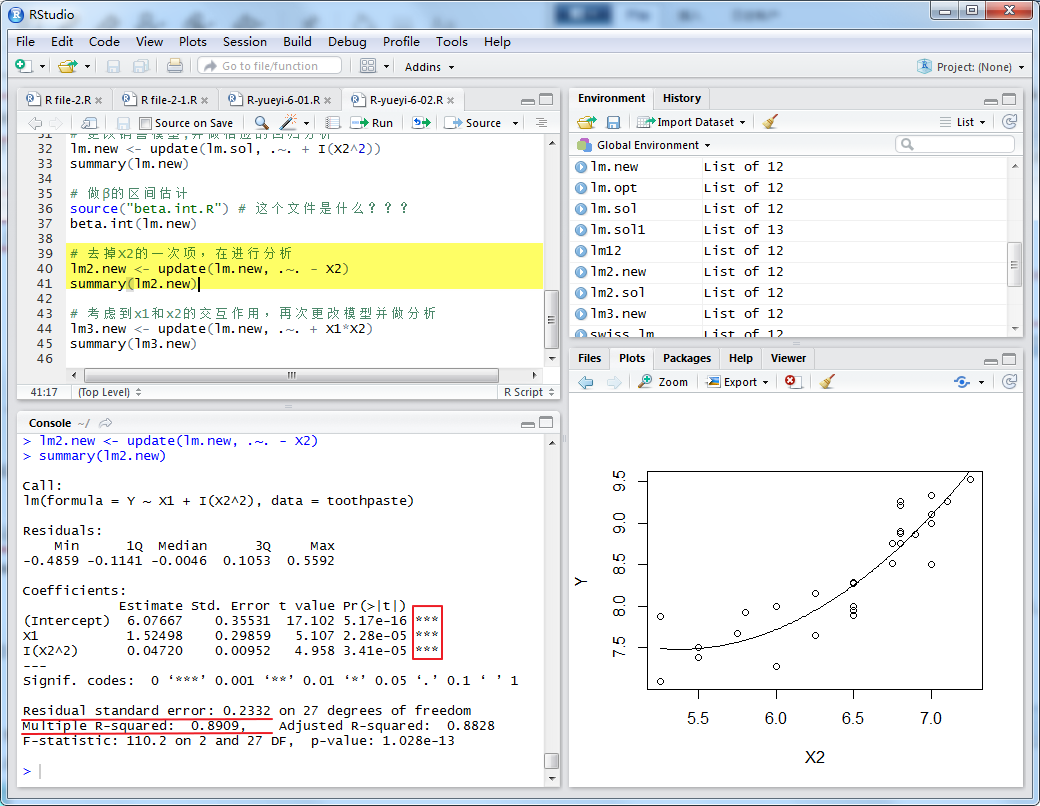
此模型雖然通過了F檢驗和T檢驗，但與上一模型對比來看，Residual standard error上升，Multiple R-squared下降。這又是此模型的不足之處。

在做進一步的修正，考慮X1和X2交互作用，及模型為：

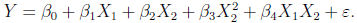
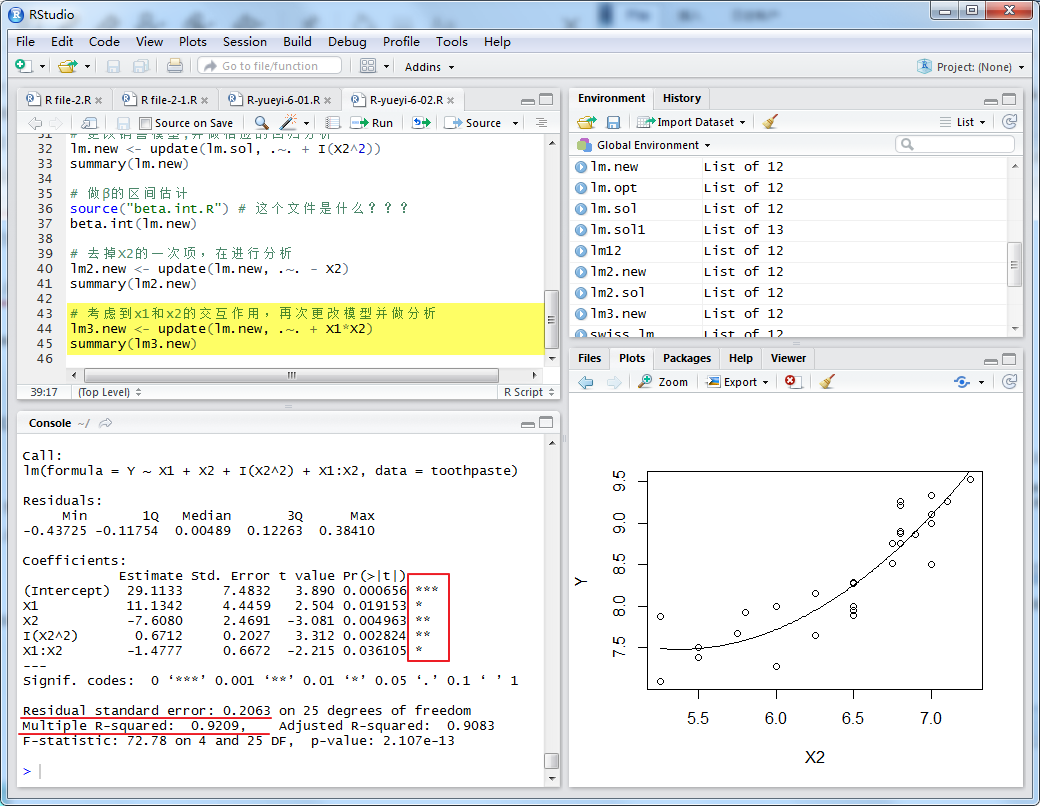
模型通過T檢驗和F檢驗，并且Residual standard error減少，Multiple R-squared增加。因此，最終模型選為：

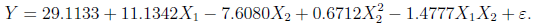
以上是“使用R語言與多元線性回歸分析計算的示例”這篇文章的所有內容，感謝各位的閱讀！相信大家都有了一定的了解，希望分享的內容對大家有所幫助，如果還想學習更多知識，歡迎關注億速云行業資訊頻道！