NumPy怎么實現多維數組中的線性代數

本篇內容介紹了“NumPy怎么實現多維數組中的線性代數”的有關知識，在實際案例的操作過程中，不少人都會遇到這樣的困境，接下來就讓小編帶領大家學習一下如何處理這些情況吧！希望大家仔細閱讀，能夠學有所成！

目錄

• 簡介
  

• 圖形加載和說明
  

• 圖形的灰度
  

• 灰度圖像的壓縮
  

• 原始圖像的壓縮
  

• 總結
  

簡介

本文將會以圖表的形式為大家講解怎么在NumPy中進行多維數據的線性代數運算。
多維數據的線性代數通常被用在圖像處理的圖形變換中，本文將會使用一個圖像的例子進行說明。

圖形加載和說明

熟悉顏色的朋友應該都知道，一個顏色可以用R，G，B來表示，如果更高級一點，那么還有一個A表示透明度。通常我們用一個四個屬性的數組來表示。

對于一個二維的圖像來說，其分辨率可以看做是一個X*Y的矩陣，矩陣中的每個點的顏色都可以用（R，G，B）來表示。

有了上面的知識，我們就可以對圖像的顏色進行分解了。

首先需要加載一個圖像，我們使用imageio.imread方法來加載一個本地圖像，如下所示：

import imageio
img=imageio.imread('img.png')
print(type(img))

上面的代碼從本地讀取圖片到img對象中，使用type可以查看img的類型，從運行結果，我們可以看到img的類型是一個數組。

class 'imageio.core.util.Array'

通過img.shape可以得到img是一個(80, 170, 4)的三維數組，也就是說這個圖像的分辨率是80*170，每個像素是一個（R，B，G，A）的數組。

最后將圖像畫出來如下所示：

import matplotlib.pyplot as plt
plt.imshow(img)

圖形的灰度

對于三維數組來說，我們可以分別得到三種顏色的數組如下所示：

red_array = img_array[:, :, 0]
green_array = img_array[:, :, 1]
blue_array = img_array[:, :, 2]

有了三個顏色之后我們可以使用下面的公式對其進行灰度變換：

Y=0.2126R + 0.7152G + 0.0722B

上圖中Y表示的是灰度。
怎么使用矩陣的乘法呢？使用 @ 就可以了：

 img_gray = img_array @ [0.2126, 0.7152, 0.0722]

現在img是一個80 * 170的矩陣。
現在使用cmap="gray"作圖：

plt.imshow(img_gray, cmap="gray")

可以得到下面的灰度圖像：

灰度圖像的壓縮

灰度圖像是對圖像的顏色進行變換，如果要對圖像進行壓縮該怎么處理呢？

矩陣運算中有一個概念叫做奇異值和特征值。

設A為n階矩陣，若存在常數λ及n維非零向量x，使得Ax=λx，則稱λ是矩陣A的特征值，x是A屬于特征值λ的特征向量。

一個矩陣的一組特征向量是一組正交向量。

即特征向量被施以線性變換 A 只會使向量伸長或縮短而其方向不被改變。

特征分解（Eigendecomposition），又稱譜分解（Spectral decomposition）是將矩陣分解為由其特征值和特征向量表示的矩陣之積的方法。

假如A是m * n階矩陣，q=min(m,n)，A*A的q個非負特征值的算術平方根叫作A的奇異值。

特征值分解可以方便的提取矩陣的特征，但是前提是這個矩陣是一個方陣。如果是非方陣的情況下，就需要用到奇異值分解了。先看下奇異值分解的定義：

A=UΣV^T

其中A是目標要分解的m * n的矩陣，U是一個 m * m的方陣，Σ 是一個m * n 的矩陣，其非對角線上的元素都是0。VTV^TVT是V的轉置，也是一個n * n的矩陣。

奇異值跟特征值類似，在矩陣Σ中也是從大到小排列，而且奇異值的減少特別的快，在很多情況下，前10%甚至1%的奇異值的和就占了全部的奇異值之和的99%以上了。也就是說，我們也可以用前r大的奇異值來近似描述矩陣。r是一個遠小于m、n的數，這樣就可以進行壓縮矩陣。

通過奇異值分解，我們可以通過更加少量的數據來近似替代原矩陣。

要想使用奇異值分解svd可以直接調用linalg.svd 如下所示：

U, s, Vt = linalg.svd(img_gray)

其中U是一個m * m矩陣，Vt是一個n * n矩陣。

在上述的圖像中，U是一個(80, 80)的矩陣，而Vt是一個(170, 170) 的矩陣。而s是一個80的數組，s包含了img中的奇異值。

如果將s用圖像來表示，我們可以看到大部分的奇異值都集中在前的部分：

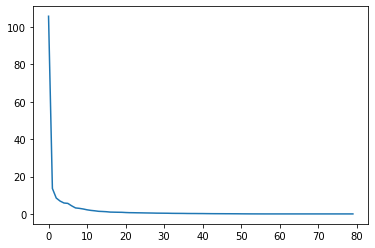
這也就意味著，我們可以取s中前面的部分值來進行圖像的重構。
使用s對圖像進行重構，需要將s還原成80 * 170 的矩陣：

# 重建
import numpy as np
Sigma = np.zeros((80, 170))
for i in range(80):
    Sigma[i, i] = s[i]

使用 U @ Sigma @ Vt 即可重建原來的矩陣，可以通過計算linalg.norm來比較一下原矩陣和重建的矩陣之間的差異。

linalg.norm(img_gray - U @ Sigma @ Vt)

或者使用np.allclose來比較兩個矩陣的不同：

np.allclose(img_gray, U @ Sigma @ Vt)

或者只取s數組的前10個元素，進行重新繪圖，比較一下和原圖的區別：

k = 10
approx = U @ Sigma[:, :k] @ Vt[:k, :]
plt.imshow(approx, cmap="gray")

可以看到，差異并不是很大：

原始圖像的壓縮

上一節我們講到了如何進行灰度圖像的壓縮，那么如何對原始圖像進行壓縮呢？

同樣可以使用linalg.svd對矩陣進行分解。

但是在使用前需要進行一些處理，因為原始圖像的img_array 是一個(80, 170, 3)的矩陣--這里我們將透明度去掉了，只保留了R，B，G三個屬性。

在進行轉換之前，我們需要把不需要變換的軸放到最前面，也就是說將index=2，換到index=0的位置，然后進行svd操作：

img_array_transposed = np.transpose(img_array, (2, 0, 1))
print(img_array_transposed.shape)

U, s, Vt = linalg.svd(img_array_transposed)
print(U.shape, s.shape, Vt.shape)

同樣的，現在s是一個(3, 80)的矩陣，還是少了一維，如果重建圖像，需要將其進行填充和處理，最后將重建的圖像輸出：

Sigma = np.zeros((3, 80, 170))

for j in range(3):
    np.fill_diagonal(Sigma[j, :, :], s[j, :])

reconstructed = U @ Sigma @ Vt
print(reconstructed.shape)

plt.imshow(np.transpose(reconstructed, (1, 2, 0)))

當然，也可以選擇前面的K個特征值對圖像進行壓縮：

approx_img = U @ Sigma[..., :k] @ Vt[..., :k, :]
print(approx_img.shape)
plt.imshow(np.transpose(approx_img, (1, 2, 0)))

重新構建的圖像如下：

對比可以發現，雖然損失了部分精度，但是圖像還是可以分辨的。

總結

圖像的變化會涉及到很多線性運算，大家可以以此文為例，仔細研究。

“NumPy怎么實現多維數組中的線性代數”的內容就介紹到這里了，感謝大家的閱讀。如果想了解更多行業相關的知識可以關注億速云網站，小編將為大家輸出更多高質量的實用文章！