您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
本篇內容介紹了“C++如何實現搜索二維矩陣功能”的有關知識,在實際案例的操作過程中,不少人都會遇到這樣的困境,接下來就讓小編帶領大家學習一下如何處理這些情況吧!希望大家仔細閱讀,能夠學有所成!
Write an efficient algorithm that searches for a value in an m x n matrix. This matrix has the following properties:
Integers in each row are sorted from left to right.
The first integer of each row is greater than the last integer of the previous row.
Example 1:
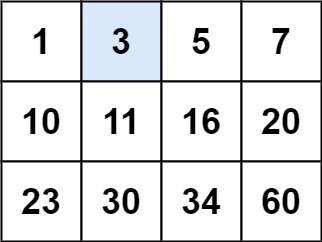
Input: matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 3
Output: true
Example 2:
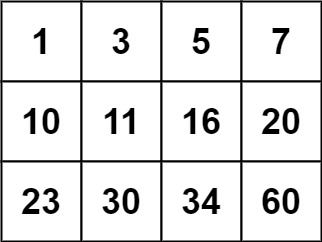
Input: matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 13
Output: false
Constraints:
m == matrix.length
n == matrix[i].length
1 <= m, n <= 100
-104 <= matrix[i][j], target <= 104
這道題要求搜索一個二維矩陣,由于給的矩陣是有序的,所以很自然的想到要用二分查找法,可以在第一列上先用一次二分查找法找到目標值所在的行的位置,然后在該行上再用一次二分查找法來找是否存在目標值。對于第一個二分查找,由于第一列的數中可能沒有 target 值,該如何查找呢,如果是查找第一個不小于目標值的數,當 target 在第一列時,會返回 target 所在的行,但若 target 不在的話,有可能會返回下一行,不好統一。所以可以查找第一個大于目標值的數,也就是總結帖中的第三類,這樣只要回退一個,就一定是 target 所在的行。但需要注意的一點是,如果返回的是0,就不能回退了,以免越界,記得要判斷一下。找到了 target 所在的行數,就可以再次使用二分搜索,此時就是總結帖中的第一類了,查找和 target 值相同的數,也是最簡單的一類,分分鐘搞定即可,參見代碼如下:
解法一:
class Solution {
public:
bool searchMatrix(vector<vector<int>>& matrix, int target) {
if (matrix.empty() || matrix[0].empty()) return false;
int left = 0, right = matrix.size();
while (left < right) {
int mid = (left + right) / 2;
if (matrix[mid][0] == target) return true;
if (matrix[mid][0] < target) left = mid + 1;
else right = mid;
}
int tmp = (right > 0) ? (right - 1) : right;
left = 0;
right = matrix[tmp].size();
while (left < right) {
int mid = (left + right) / 2;
if (matrix[tmp][mid] == target) return true;
if (matrix[tmp][mid] < target) left = mid + 1;
else right = mid;
}
return false;
}
};當然這道題也可以使用一次二分查找法,如果我們按S型遍歷該二維數組,可以得到一個有序的一維數組,只需要用一次二分查找法,而關鍵就在于坐標的轉換,如何把二維坐標和一維坐標轉換是關鍵點,把一個長度為n的一維數組轉化為 m*n 的二維數組 (m*n = n)后,那么原一維數組中下標為i的元素將出現在二維數組中的 [i/n][i%n] 的位置,有了這一點,代碼很好寫出來了:
解法二:
class Solution {
public:
bool searchMatrix(vector<vector<int>>& matrix, int target) {
if (matrix.empty() || matrix[0].empty()) return false;
int m = matrix.size(), n = matrix[0].size();
int left = 0, right = m * n;
while (left < right) {
int mid = (left + right) / 2;
if (matrix[mid / n][mid % n] == target) return true;
if (matrix[mid / n][mid % n] < target) left = mid + 1;
else right = mid;
}
return false;
}
};這道題其實也可以不用二分搜索法,直接使用雙指針也是可以的,i指向0,j指向列數,這樣第一個被驗證的數就是二維數組右上角的數字,假如這個數字等于 target,直接返回 true;若大于 target,說明要減小數字,則列數j自減1;若小于 target,說明要增加數字,行數i自增1。若 while 循環退出了還是沒找到 target,直接返回 false 即可,參見代碼如下:
解法三:
class Solution {
public:
bool searchMatrix(vector<vector<int>>& matrix, int target) {
if (matrix.empty() || matrix[0].empty()) return false;
int i = 0, j = (int)matrix[0].size() - 1;
while (i < matrix.size() && j >= 0) {
if (matrix[i][j] == target) return true;
else if (matrix[i][j] > target) --j;
else ++i;
}
return false;
}
};“C++如何實現搜索二維矩陣功能”的內容就介紹到這里了,感謝大家的閱讀。如果想了解更多行業相關的知識可以關注億速云網站,小編將為大家輸出更多高質量的實用文章!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。