您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
這篇文章主要講解了“Python數學建模中整數規劃的原理及應用”,文中的講解內容簡單清晰,易于學習與理解,下面請大家跟著小編的思路慢慢深入,一起來研究和學習“Python數學建模中整數規劃的原理及應用”吧!
一、從線性規劃到整數規劃
1.1、為什么會有整數規劃?
1.2、四舍五入就能得到整數解嗎?
二、整數規劃的求解方法
2.1、分支定界法(Branch and bound)
2.2、割平面法(Cutting plane)
2.3、整數規劃的編程方案
三、PuLP 求解整數規劃問題
3.1、案例問題描述
3.2、建模過程分析
3.2.1、問題定義
3.2.2、模型構建
3.2.3、模型求解
3.3、Python 例程
3.4、Python 例程運行結果
線性規劃問題的最優解可能是分數或小數。整數規劃是指變量的取值只能是整數的規劃。
這在實際問題中很常見,例如車間人數、設備臺數、行駛次數,這些變量顯然必須取整數解。
根據對變量的不同情況,整數規劃又可以分為:
完全整數規劃,全部變量都要求是整數;
混合整數規劃,部分變量要求是整數;
0-1整數規劃,變量的取值只能是 0 或 1;
混合0-1規劃,部分變量的取值只能是 0 或 1。
0-1整數規劃 是非常重要也非常特殊的整數規劃,需要在另外的文章進行討論。
整數規劃問題與線性規劃問題的區別只是增加了整數約束。這看上去好像只要把線性規劃得到的非整數解舍入化整,就可以得到整數解,并不是多么復雜的問題。
但是問題并沒有這么簡單。化整后的解不僅不一定是最優解,甚至不一定是可行解的——線性規劃的最優解,取整后可能就不滿足約束條件了。
那么,不要按四舍五入取整,而是向滿足約束條件的方向取整,是不是就可以呢?這是很好的想法,通常這樣可以獲得可行解,但卻不一定是最優解了。
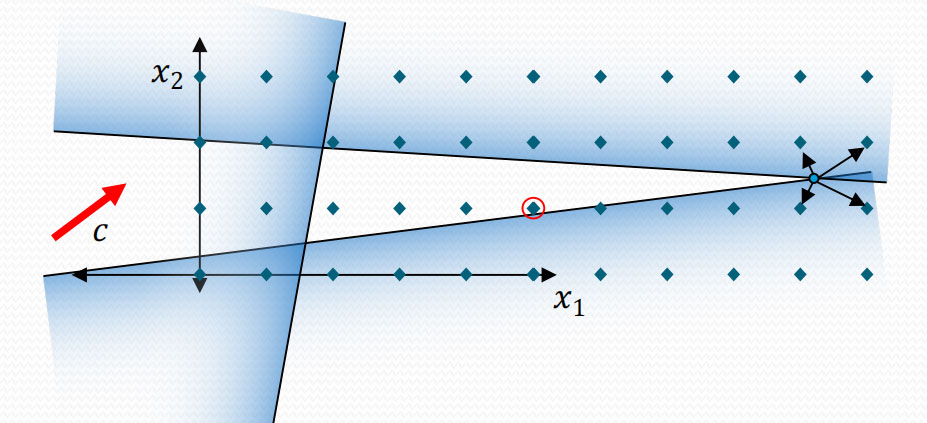
因此,整數規劃問題比線性規劃復雜的多,以至于至今還沒有通用的多項式解法,也就是說算法復雜度與問題規模成指數關系(NP問題)。還沒有意識到與問題規模指數關系意味著什么嗎?就是那個在象棋棋盤上放麥子,每格比前一格加倍的故事。
問題區別一點點,難度卻相差千萬里。小白與學霸,差距其實并不大。
分支定界法的基本思想是把原問題(整數規劃問題)轉換為一個個線性規劃問題來處理,并在求解這些線性規劃問題的過程中不斷追蹤原問題的上界(最優可行解)和下界(最優線性松弛解)。
分支定界法把全部可行解空間反復地分割為越來越小的子集,稱為分枝;并且對每個子集內的解集計算一個目標上界,稱為定界。每次分枝后,對于超出已知可行解集目標值的那些子集不再進一步分枝,就可以刪減很多子集,這稱為剪枝。
數學課代表的說法是:設有最大化的整數規劃問題 A,先解與之相應的線性規劃問題 B,若 B 的最優解不符合 A 的整數條件,則 B 的最優目標函數必是 A 的最優目標函數 z 的上界,記為 z2,而 A 的任意可行解的目標函數值將是 z 的一個下界 z1。分支定界法就是將 B 的可行域分成子區域(分支)的方法,逐步減小 z2 和增大 z1,最終求到 z*。
分支定界法是一個迭代算法,隨著迭代過程不斷更新上界和下界,直到上界和下界非常接近時結束。通常設置 Gap < 0.1%,就可把當前的最優可行解近似為問題的全局最優解了。因此,分支定界法的“收斂” 不是分析意義上的而是算法意義上的,優化結果是近似解而不是精確解。
分支定界法不用區分完全整數規劃與混合整數規劃,算法便于實現,但計算量比較大。
割平面法的基本思路是先求解普通線性規劃問題的最優解,再對非整數解添加約束條件使可行域縮小,如此反復求解添加了約束條件的普通線性規劃問題,直到得到整數解。
也就是說,先不考慮整數約束條件,直接求解松弛問題的最優解,如果滿足整數條件就結束了,如果不滿足整數條件,就在此非整數解的基礎上增加新的約束條件重新求解。這個新增加的約束條件稱為割平面,對松弛問題的可行域割一刀,割去松弛問題的部分非整數解。經過有限次的反復切割,必定可在縮小的可行域的一個整數極點上達到整數規劃問題的最優解 。
割平面法的計算量比較小,但對問題的結構及求解的要求較高,算法比較復雜。
在各種算法的介紹和評價中,有時會說“算法比較簡單,編程比較容易”。對此小白千萬不要當真。不論分支定界法還是割平面法,小白不要說自己按照算法步驟一步步編程實現,就是給你現成的程序估計你也看不懂的。這很正常,就算大神也沒幾個人能看懂哪怕是自己寫出來的算法。
但是如果給你程序也不會使用,那就是問題了。不幸的是,這是數學建模學習和參賽中經常遇到的問題:有了調試好的程序,例程運行結果也正常,但換個問題仍然不會使用。
這并不是你的錯。程序有漏洞,接口不標準,文檔對不上,教程說不清,這就是你所拿到的例程。你的錯誤,是選擇了這樣的例程,或者說選擇了這樣的編程方案。
這也是本系列教程希望解決的問題。就拿線性規劃、整數規劃來說,算法還不是很復雜,第三方軟件包也很豐富。但是,Scipy 只能求解線性規劃,不能求解整數規劃,如果選擇 Scipy 做線性規劃,那在學整數規劃時就要再學另一種工具包,二者的模型描述、函數定義、參數設置肯定也是不同的。接下來遇到非線性規劃問題再學一種軟件包,最后別說熟練掌握算法函數,連什么時候該用哪個 工具包都搞暈了。
閑話少說,我們還是用上節求解線性規劃問題的 PuLP 工具包。
我們不僅繼續用 PuLP 工具包,而且解題過程和編程步驟也與求解線性規劃問題完全一致。
下面我們以一個簡單的數學模型練習,來講解整個解題過程,而不僅給出例程。
例題 1:
某廠生產甲乙兩種飲料,每百箱甲飲料需用原料 6千克、工人 10名,獲利 10萬元;每百箱乙飲料需用原料 5千克、工人 20名,獲利 9萬元。
今工廠共有原料 60千克、工人 150名,又由于其他條件所限甲飲料產量不超過8百箱。
問題 1:問如何安排生產計劃,即兩種飲料各生產多少使獲利最大?
問題 2:若投資0.8萬元可增加原料1千克,是否應作這項投資?投資多少合理?
問題 3:若不允許散箱(按整百箱生產),如何安排生產計劃,即兩種飲料各生產多少使獲利最大?
問題 4:若不允許散箱(按整百箱生產),若投資0.8萬元可增加原料1千克,是否應作這項投資?投資多少合理?
線性規劃和整數規劃類的問題的建模和求解,通常可以按問題定義、模型構建、模型求解的步驟進行。
問題定義, 確定決策變量、目標函數和約束條件。
1.決策變量是問題中可以在一定范圍內進行變化而獲得不同結果的變量。
對于問題 1,問題描述中說的很明確,希望通過改變甲、乙兩種飲料的產量使總利潤最大,甲、乙兩種飲料的產量就是決策變量。
對于問題 2 則要注意,如果只看前一句,就是比較問題 1 與問題 2 的利潤,還是把甲、乙兩種飲料的產量作為決策變量。但要回答后一句“投資多少合理”,這就出現了一個新的變量“投資額”,因此對問題 2 要建立 3個決策變量:甲產量、乙產量和投資額。
2.目標函數是決策變量的函數,我們希望通過改變決策變量的值而獲得目標函數的最大值或最小值,通常是總成本(最小)、總利潤(最大)、總時間(最短)。
對于本案例,每個問題都是希望獲得最大利潤,目標函數都是總利潤,問題是求目標函數即總利潤的最大值。
3.約束條件是決策變量所要滿足的限制條件。
約束條件 3 種情況:
一是不等式約束,例如題目指出共有原料 60千克、工人 150名,因此生產計劃所用的原料、工人的需求不能大于題目中數值。
二是等式約束,本題沒有等式約束條件。
三是決策變量取值范圍的約束。
通常,題目隱含著決策變量大于等于 0 的條件,例如工人人數、原料數量都要大于等于 0。
另外,如果能通過分析前面的等式約束或不等式約束,得出決策變量的上限,將會極大的提高問題求解的速度和性能。后文將對此舉例說明。
模型構建, 由問題描述建立數學方程,并轉化為標準形式的數學模型。
對于問題 1,目標函數是生產甲、乙兩種飲料的總利潤,約束條件是原料總量、工人總數的約束,而且原料、工人都要大于等于 0。
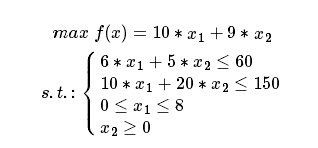
進一步分析決策變量取值范圍的約束條件,由原料數量、工人數量的不等式約束可以推出:
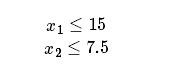
對于問題 2,可以通過增加投資來獲得更多的原料,投資額是一個新的變量。要注意的是,此時目標函數雖然也是生產兩種飲料的總利潤,但總利潤不等于總收入,而是總收入減去總成本,在本例中就是要減去購買原料的投資。
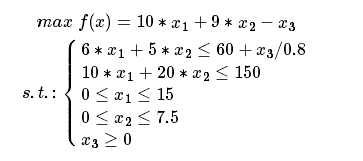
對于問題 3 和問題 4,區別只是不允許散箱,明確提出了決策變量 x1、x2 的取值要取整數值,所以是整數規劃問題。
需要注意的是,問題 4 中對增加的投資額即購買的原料數量并沒有整數限制,因此 x1、x2 的取值范圍是正整數,但 x3 的取值范圍是正數,這是一個混合整數規劃問題。
還要說明的是,對于問題 1 和問題 2,雖然題目中沒有明確要求生產甲、乙飲料的工人人數為整數,但是人數也不可能是小數的,那么這是不是也是整數規劃問題呢?
如果你能提出這個問題,那么恭喜你,你已經從小白升級為菜鳥了。
我的理解是,這個問題怎么說都可以。如果要簡化問題,使用線性規劃模型,最好在問題假設中說一句,假設甲乙飲料在同一車間先后生產,只要允許甲乙飲料散箱生產,即使根據產量所求出的工人數是小數,也可以解釋的通。如果你掌握了整數規劃問題的求解,那就先按線性規劃建模,再補充討論工人人數也必須是整數的條件,按整數規劃建模求解,這就是妥妥的獲獎論文了。
模型求解,用標準模型的優化算法對模型求解,得到優化結果。
在線性規劃問題中已經講過使用 PuLP 的求解步驟:
(0)導入 PuLP庫函數
import pulp
(1)定義一個規劃問題
ProbLP1 = pulp.LpProblem("ProbLP1", sense=pulp.LpMaximize) # 定義問題 1,求最大值pulp.LpProblem 用來定義問題的構造函數。"ProbLP1"是用戶定義的問題名。
參數 sense 指定問題求目標函數的最小值/最大值 。本例求最大值,選擇 “pulp.LpMaximize” 。
(2)定義決策變量
對于問題 1:
x1 = pulp.LpVariable('x1', lowBound=0, upBound=15, cat='Continuous') # 定義 x1
x2 = pulp.LpVariable('x2', lowBound=0, upBound=7.5, cat='Continuous') # 定義 x2pulp.LpVariable 用來定義決策變量的函數。'x1'、'x2' 是用戶定義的變量名。
參數 lowBound、upBound 用來設定決策變量的下界、上界;可以不定義下界/上界,默認的下界/上界是負無窮/正無窮。本例中 x1、x2 的取值區間分別為 [0,15]、[0,7.5]。
參數 cat 用來設定變量類型,可選參數值:'Continuous' 表示連續變量(默認值)、' Integer ' 表示離散變量(用于整數規劃問題)、' Binary ' 表示0/1變量(用于0/1規劃問題)。
對于問題 3, 甲乙飲料產量 x1、x2 必須取整數,是整數規劃問題,因此要設置變量類型為離散變量(整數變量):
x1 = pulp.LpVariable('x1', lowBound=0, upBound=15, cat='Integer') # 定義 x1,變量類型:整數
x2 = pulp.LpVariable('x2', lowBound=0, upBound=7.5, cat='Integer') # 定義 x2,變量類型:整數(3)添加目標函數
ProbLP1 += (10*x1 + 9*x2) # 設置目標函數 f(x)
添加目標函數使用 "問題名 += 目標函數式" 格式。
(4)添加約束條件
ProbLP1 += (6*x1 + 5*x2 <= 60) # 不等式約束 ProbLP1 += (10*x1 + 20*x2 <= 150) # 不等式約束
添加約束條件使用 "問題名 += 約束條件表達式" 格式。
約束條件可以是等式約束或不等式約束,不等式約束可以是 小于等于 或 大于等于,分別使用關鍵字">="、"<="和"=="。
(5)求解
ProbLP1.solve()
print(ProbLP1.name) # 輸出求解狀態
print("Status:", pulp.LpStatus[ProbLP1.status]) # 輸出求解狀態
for v in ProbLP1.variables():
print(v.name, "=", v.varValue) # 輸出每個變量的最優值
print("F1(x) =", pulp.value(ProbLP1.objective)) # 輸出最優解的目標函數值solve() 是求解函數,可以對求解器、求解精度進行設置。
PuLP默認采用 CBC 求解器來求解優化問題,也可以調用其它的優化器來求解,但需要另外安裝。
import pulp # 導入 pulp 庫
# 主程序
def main():
# 模型參數設置
"""
問題描述:
某廠生產甲乙兩種飲料,每百箱甲飲料需用原料6千克、工人10名,獲利10萬元;每百箱乙飲料需用原料5千克、工人20名,獲利9萬元。
今工廠共有原料60千克、工人150名,又由于其他條件所限甲飲料產量不超過8百箱。
(1)問如何安排生產計劃,即兩種飲料各生產多少使獲利最大?
(2)若投資0.8萬元可增加原料1千克,是否應作這項投資?投資多少合理?
(3)若不允許散箱(按整百箱生產),如何安排生產計劃,即兩種飲料各生產多少使獲利最大?
(4)若不允許散箱(按整百箱生產),若投資0.8萬元可增加原料1千克,是否應作這項投資?投資多少合理?
"""
# 問題 1:
"""
問題建模:
決策變量:
x1:甲飲料產量(單位:百箱)
x2:乙飲料產量(單位:百箱)
目標函數:
max fx = 10*x1 + 9*x2
約束條件:
6*x1 + 5*x2 <= 60
10*x1 + 20*x2 <= 150
x1, x2 >= 0,x1 <= 8
此外,由 x1,x2>=0 和 10*x1+20*x2<=150 可知 0<=x2<=7.5
"""
ProbLP1 = pulp.LpProblem("ProbLP1", sense=pulp.LpMaximize) # 定義問題 1,求最大值
x1 = pulp.LpVariable('x1', lowBound=0, upBound=8, cat='Continuous') # 定義 x1
x2 = pulp.LpVariable('x2', lowBound=0, upBound=7.5, cat='Continuous') # 定義 x2
ProbLP1 += (10*x1 + 9*x2) # 設置目標函數 f(x)
ProbLP1 += (6*x1 + 5*x2 <= 60) # 不等式約束
ProbLP1 += (10*x1 + 20*x2 <= 150) # 不等式約束
ProbLP1.solve()
print(ProbLP1.name) # 輸出求解狀態
print("Status youcans:", pulp.LpStatus[ProbLP1.status]) # 輸出求解狀態
for v in ProbLP1.variables():
print(v.name, "=", v.varValue) # 輸出每個變量的最優值
print("F1(x) =", pulp.value(ProbLP1.objective)) # 輸出最優解的目標函數值
# 問題 2:
"""
問題建模:
決策變量:
x1:甲飲料產量(單位:百箱)
x2:乙飲料產量(單位:百箱)
x3:增加投資(單位:萬元)
目標函數:
max fx = 10*x1 + 9*x2 - x3
約束條件:
6*x1 + 5*x2 <= 60 + x3/0.8
10*x1 + 20*x2 <= 150
x1, x2, x3 >= 0,x1 <= 8
此外,由 x1,x2>=0 和 10*x1+20*x2<=150 可知 0<=x2<=7.5
"""
ProbLP2 = pulp.LpProblem("ProbLP2", sense=pulp.LpMaximize) # 定義問題 2,求最大值
x1 = pulp.LpVariable('x1', lowBound=0, upBound=8, cat='Continuous') # 定義 x1
x2 = pulp.LpVariable('x2', lowBound=0, upBound=7.5, cat='Continuous') # 定義 x2
x3 = pulp.LpVariable('x3', lowBound=0, cat='Continuous') # 定義 x3
ProbLP2 += (10*x1 + 9*x2 - x3) # 設置目標函數 f(x)
ProbLP2 += (6*x1 + 5*x2 - 1.25*x3 <= 60) # 不等式約束
ProbLP2 += (10*x1 + 20*x2 <= 150) # 不等式約束
ProbLP2.solve()
print(ProbLP2.name) # 輸出求解狀態
print("Status youcans:", pulp.LpStatus[ProbLP2.status]) # 輸出求解狀態
for v in ProbLP2.variables():
print(v.name, "=", v.varValue) # 輸出每個變量的最優值
print("F2(x) =", pulp.value(ProbLP2.objective)) # 輸出最優解的目標函數值
# 問題 3:整數規劃問題
"""
問題建模:
決策變量:
x1:甲飲料產量,正整數(單位:百箱)
x2:乙飲料產量,正整數(單位:百箱)
目標函數:
max fx = 10*x1 + 9*x2
約束條件:
6*x1 + 5*x2 <= 60
10*x1 + 20*x2 <= 150
x1, x2 >= 0,x1 <= 8,x1, x2 為整數
此外,由 x1,x2>=0 和 10*x1+20*x2<=150 可知 0<=x2<=7.5
"""
ProbLP3 = pulp.LpProblem("ProbLP3", sense=pulp.LpMaximize) # 定義問題 3,求最大值
print(ProbLP3.name) # 輸出求解狀態
x1 = pulp.LpVariable('x1', lowBound=0, upBound=8, cat='Integer') # 定義 x1,變量類型:整數
x2 = pulp.LpVariable('x2', lowBound=0, upBound=7.5, cat='Integer') # 定義 x2,變量類型:整數
ProbLP3 += (10 * x1 + 9 * x2) # 設置目標函數 f(x)
ProbLP3 += (6 * x1 + 5 * x2 <= 60) # 不等式約束
ProbLP3 += (10 * x1 + 20 * x2 <= 150) # 不等式約束
ProbLP3.solve()
print("Shan Status:", pulp.LpStatus[ProbLP3.status]) # 輸出求解狀態
for v in ProbLP3.variables():
print(v.name, "=", v.varValue) # 輸出每個變量的最優值
print("F3(x) =", pulp.value(ProbLP3.objective)) # 輸出最優解的目標函數值
# 問題 4:
"""
問題建模:
決策變量:
x1:甲飲料產量,正整數(單位:百箱)
x2:乙飲料產量,正整數(單位:百箱)
x3:增加投資(單位:萬元)
目標函數:
max fx = 10*x1 + 9*x2 - x3
約束條件:
6*x1 + 5*x2 <= 60 + x3/0.8
10*x1 + 20*x2 <= 150
x1, x2, x3 >= 0,x1 <= 8,x1, x2 為整數
此外,由 x1,x2>=0 和 10*x1+20*x2<=150 可知 0<=x2<=7.5
"""
ProbLP4 = pulp.LpProblem("ProbLP4", sense=pulp.LpMaximize) # 定義問題 4,求最大值
print(ProbLP4.name) # 輸出求解狀態
x1 = pulp.LpVariable('x1', lowBound=0, upBound=8, cat='Integer') # 定義 x1,變量類型:整數
x2 = pulp.LpVariable('x2', lowBound=0, upBound=7, cat='Integer') # 定義 x2,變量類型:整數
x3 = pulp.LpVariable('x3', lowBound=0, cat='Continuous') # 定義 x3
ProbLP4 += (10*x1 + 9*x2 - x3) # 設置目標函數 f(x)
ProbLP4 += (6*x1 + 5*x2 - 1.25*x3 <= 60) # 不等式約束
ProbLP4 += (10*x1 + 20*x2 <= 150) # 不等式約束
ProbLP4.solve()
print("Shan Status:", pulp.LpStatus[ProbLP4.status]) # 輸出求解狀態
for v in ProbLP4.variables():
print(v.name, "=", v.varValue) # 輸出每個變量的最優值
print("F4(x) =", pulp.value(ProbLP4.objective)) # 輸出最優解的目標函數值
return
if __name__ == '__main__': # Copyright 2021 YouCans, XUPT
main()Welcome to the CBC MILP Solver
Version: 2.9.0
Build Date: Feb 12 2015
ProbLP1
Status: Optimal
x1 = 6.4285714
x2 = 4.2857143
F1(x) = 102.8571427
ProbLP2
Status: Optimal
x1 = 8.0
x2 = 3.5
x3 = 4.4
F2(x) = 107.1
ProbLP3
Result - Optimal solution found
Status Shan: Optimal
Status: Optimal
x1 = 8.0
x2 = 2.0
F3(x) = 98.0
ProbLP4
Result - Optimal solution found
Status: Optimal
x1 = 8.0
x2 = 3.0
x3 = 2.4
F4(x) = 104.6
感謝各位的閱讀,以上就是“Python數學建模中整數規劃的原理及應用”的內容了,經過本文的學習后,相信大家對Python數學建模中整數規劃的原理及應用這一問題有了更深刻的體會,具體使用情況還需要大家實踐驗證。這里是億速云,小編將為大家推送更多相關知識點的文章,歡迎關注!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。