FP Tree算法原理是什么

FP Tree算法原理是什么，相信很多沒有經驗的人對此束手無策，為此本文總結了問題出現的原因和解決方法，通過這篇文章希望你能解決這個問題。

Apriori算法是挖掘頻繁項集的經典算法，需要多次掃描數據，I/O是很大的瓶頸。為了解決這個問題，FP Tree算法（也稱FP Growth算法）采用了一些技巧，無論多少數據，只需要掃描兩次數據集，因此提高了算法運行的效率。下面我們就對FP Tree算法做一個總結。

1. FP Tree數據結構

　　　　為了減少I/O次數，FP Tree算法引入了一些數據結構來臨時存儲數據。這個數據結構包括三部分，如下圖所示：

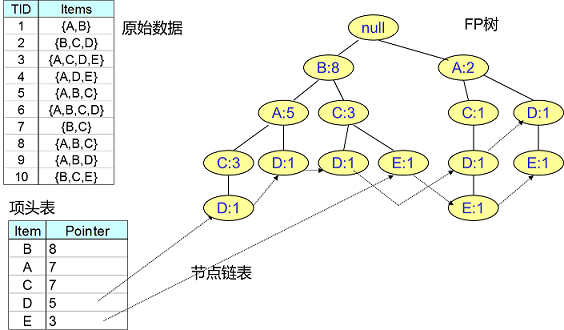
　　　　第一部分是一個項頭表。里面記錄了所有的1項頻繁集出現的次數，按照次數降序排列。比如上圖中B在所有10組數據中出現了8次，因此排在第一位，這部分好理解。第二部分是FP Tree，它將我們的原始數據集映射到了內存中的一顆FP樹，這個FP樹比較難理解，它是怎么建立的呢？這個我們后面再講。第三部分是節點鏈表。所有項頭表里的1項頻繁集都是一個節點鏈表的頭，它依次指向FP樹中該1項頻繁集出現的位置。這樣做主要是方便項頭表和FP Tree之間的聯系查找和更新，也好理解。

　　　　下面我們講項頭表和FP樹的建立過程。

2. 項頭表的建立

　　　　FP樹的建立需要首先依賴項頭表的建立。首先我們看看怎么建立項頭表。

　　　　我們第一次掃描數據，得到所有頻繁一項集的的計數。然后刪除支持度低于閾值的項，將1項頻繁集放入項頭表，并按照支持度降序排列。接著第二次也是最后一次掃描數據，將讀到的原始數據剔除非頻繁1項集，并按照支持度降序排列。

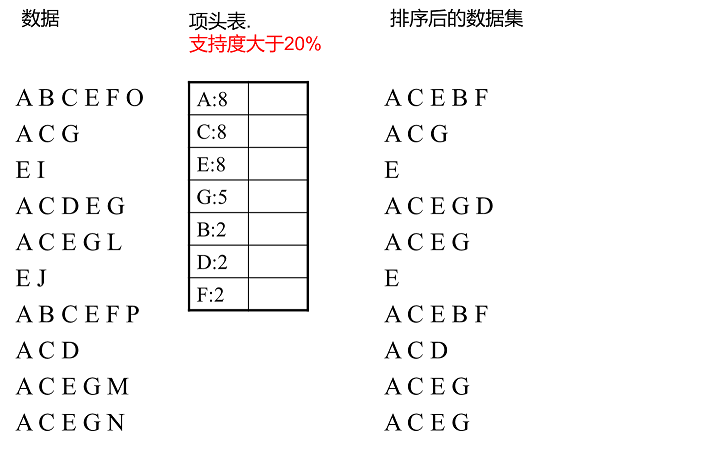
　　　　上面這段話很抽象，我們用下面這個例子來具體講解。我們有10條數據，首先第一次掃描數據并對1項集計數，我們發現O，I，L，J，P，M, N都只出現一次，支持度低于20%的閾值，因此他們不會出現在下面的項頭表中。剩下的A,C,E,G,B,D,F按照支持度的大小降序排列，組成了我們的項頭表。

　　　　接著我們第二次掃描數據，對于每條數據剔除非頻繁1項集，并按照支持度降序排列。比如數據項ABCEFO，里面O是非頻繁1項集，因此被剔除，只剩下了ABCEF。按照支持度的順序排序，它變成了ACEBF。其他的數據項以此類推。為什么要將原始數據集里的頻繁1項數據項進行排序呢？這是為了我們后面的FP樹的建立時，可以盡可能的共用祖先節點。

　　　　通過兩次掃描，項頭表已經建立，排序后的數據集也已經得到了，下面我們再看看怎么建立FP樹。

3. FP Tree的建立

　　　　有了項頭表和排序后的數據集，我們就可以開始FP樹的建立了。開始時FP樹沒有數據，建立FP樹時我們一條條的讀入排序后的數據集，插入FP樹，插入時按照排序后的順序，插入FP樹中，排序靠前的節點是祖先節點，而靠后的是子孫節點。如果有共用的祖先，則對應的公用祖先節點計數加1。插入后，如果有新節點出現，則項頭表對應的節點會通過節點鏈表鏈接上新節點。直到所有的數據都插入到FP樹后，FP樹的建立完成。

　　　　似乎也很抽象，我們還是用第二節的例子來描述。

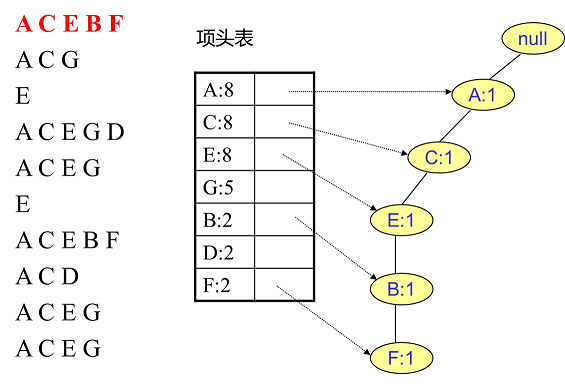
　　　　首先，我們插入第一條數據ACEBF，如下圖所示。此時FP樹沒有節點，因此ACEBF是一個獨立的路徑，所有節點計數為1, 項頭表通過節點鏈表鏈接上對應的新增節點。

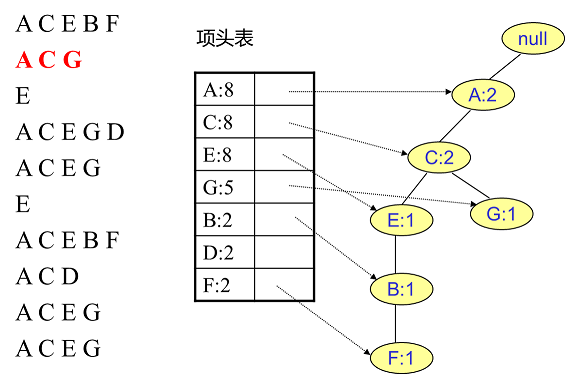
　　　　接著我們插入數據ACG，如下圖所示。由于ACG和現有的FP樹可以有共有的祖先節點序列AC，因此只需要增加一個新節點G，將新節點G的計數記為1。同時A和C的計數加1成為2。當然，對應的G節點的節點鏈表要更新

　　　　同樣的辦法可以更新后面8條數據，如下8張圖。由于原理類似，這里就不多文字講解了，大家可以自己去嘗試插入并進行理解對比。相信如果大家自己可以獨立的插入這10條數據，那么FP樹建立的過程就沒有什么難度了。

4. FP Tree的挖掘

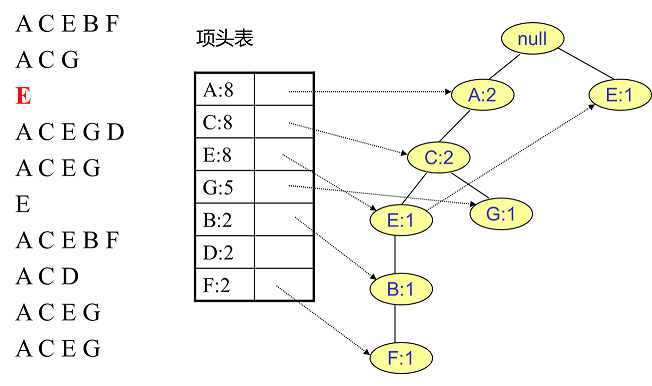
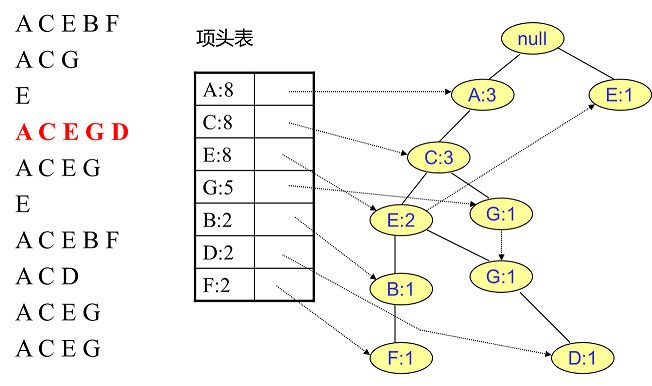
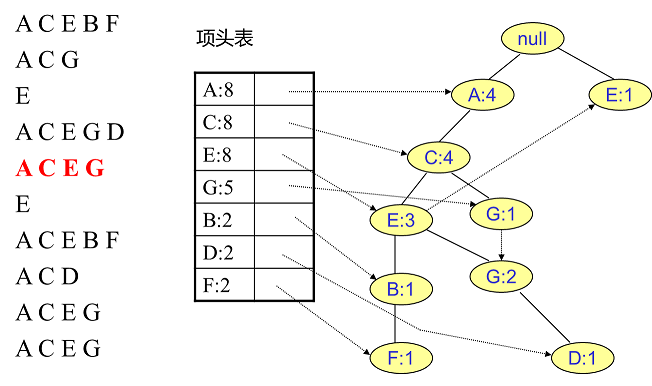
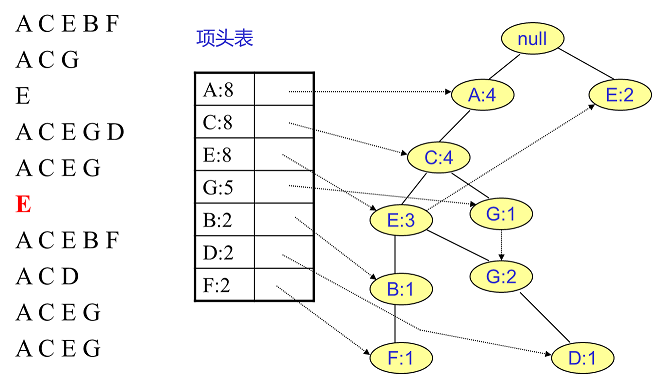
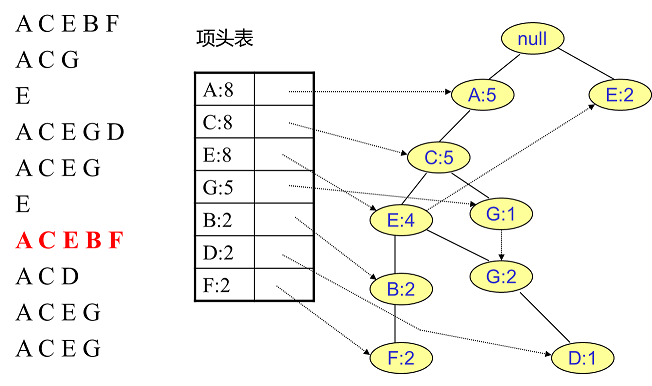
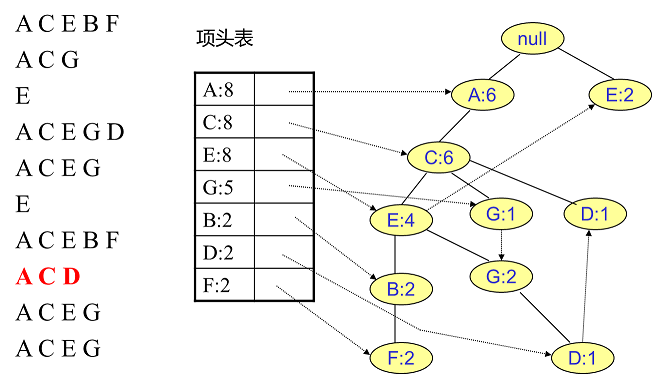
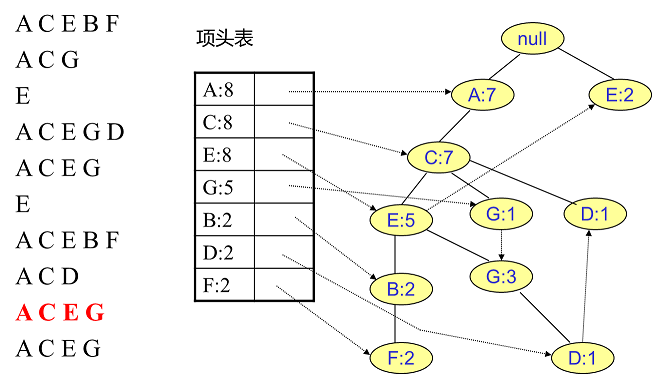
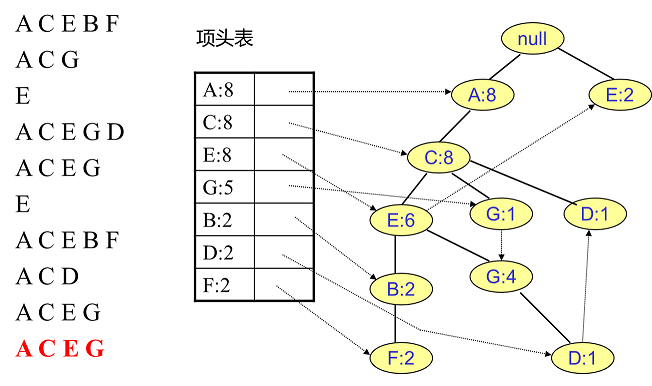
　　　　我們辛辛苦苦，終于把FP樹建立起來了，那么怎么去挖掘頻繁項集呢？看著這個FP樹，似乎還是不知道怎么下手。下面我們講如何從FP樹里挖掘頻繁項集。得到了FP樹和項頭表以及節點鏈表，我們首先要從項頭表的底部項依次向上挖掘。對于項頭表對應于FP樹的每一項，我們要找到它的條件模式基。所謂條件模式基是以我們要挖掘的節點作為葉子節點所對應的FP子樹。得到這個FP子樹，我們將子樹中每個節點的的計數設置為葉子節點的計數，并刪除計數低于支持度的節點。從這個條件模式基，我們就可以遞歸挖掘得到頻繁項集了。

　　　　實在太抽象了，之前我看到這也是一團霧水。還是以上面的例子來講解。我們看看先從最底下的F節點開始，我們先來尋找F節點的條件模式基，由于F在FP樹中只有一個節點，因此候選就只有下圖左所示的一條路徑，對應{A:8,C:8,E:6,B:2, F:2}。我們接著將所有的祖先節點計數設置為葉子節點的計數，即FP子樹變成{A:2,C:2,E:2,B:2, F:2}。一般我們的條件模式基可以不寫葉子節點，因此最終的F的條件模式基如下圖右所示。

　　　　通過它，我們很容易得到F的頻繁2項集為{A:2,F:2}, {C:2,F:2}, {E:2,F:2}, {B:2,F:2}。遞歸合并二項集，得到頻繁三項集為{A:2,C:2,F:2}，{A:2,E:2,F:2},...還有一些頻繁三項集，就不寫了。當然一直遞歸下去，最大的頻繁項集為頻繁5項集，為{A:2,C:2,E:2,B:2,F:2}

　　　　F挖掘完了，我們開始挖掘D節點。D節點比F節點復雜一些，因為它有兩個葉子節點，因此首先得到的FP子樹如下圖左。我們接著將所有的祖先節點計數設置為葉子節點的計數，即變成{A:2, C:2,E:1 G:1,D:1, D:1}此時E節點和G節點由于在條件模式基里面的支持度低于閾值，被我們刪除，最終在去除低支持度節點并不包括葉子節點后D的條件模式基為{A:2, C:2}。通過它，我們很容易得到D的頻繁2項集為{A:2,D:2}, {C:2,D:2}。遞歸合并二項集，得到頻繁三項集為{A:2,C:2,D:2}。D對應的最大的頻繁項集為頻繁3項集。

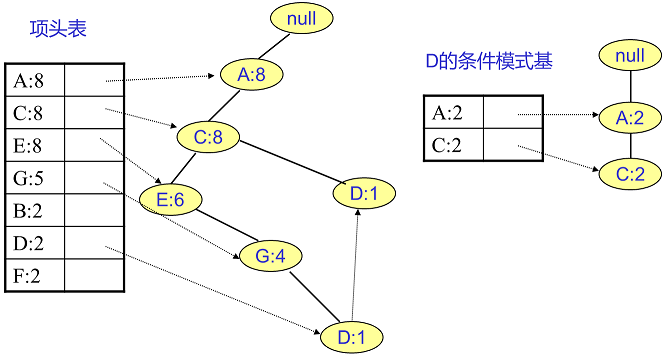
　　　　同樣的方法可以得到B的條件模式基如下圖右邊，遞歸挖掘到B的最大頻繁項集為頻繁4項集{A:2, C:2, E:2,B:2}。

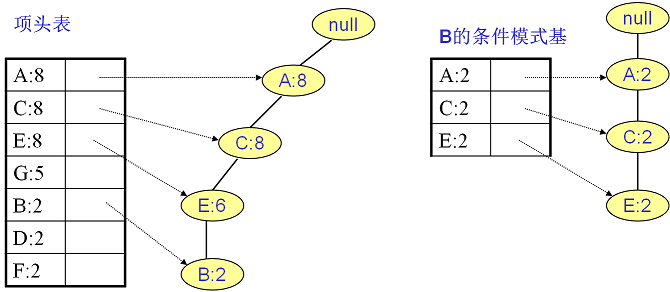
　　　　繼續挖掘G的頻繁項集，挖掘到的G的條件模式基如下圖右邊，遞歸挖掘到G的最大頻繁項集為頻繁4項集{A:5, C:5, E:4,G:4}。

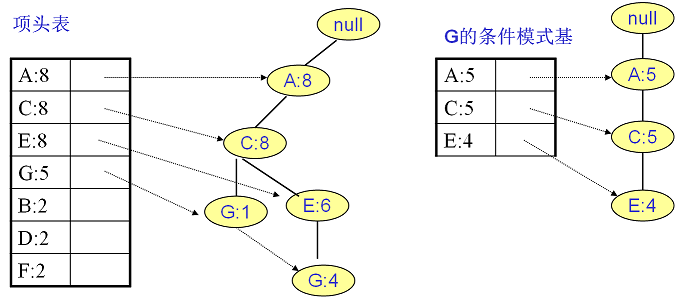
　　　　E的條件模式基如下圖右邊，遞歸挖掘到E的最大頻繁項集為頻繁3項集{A:6, C:6, E:6}。

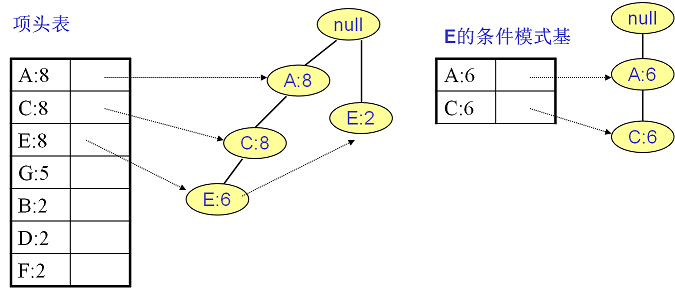
　　　　C的條件模式基如下圖右邊，遞歸挖掘到C的最大頻繁項集為頻繁2項集{A:8, C:8}。

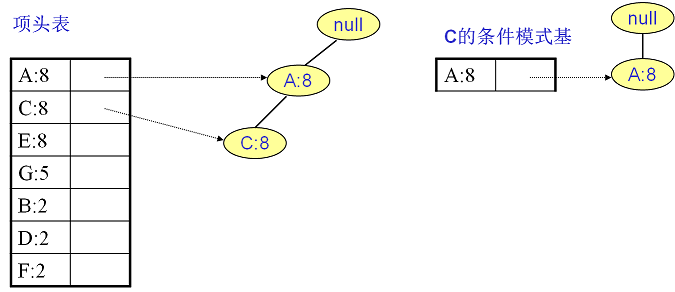
　　　　至于A，由于它的條件模式基為空，因此可以不用去挖掘了。

　　　　至此我們得到了所有的頻繁項集，如果我們只是要最大的頻繁K項集，從上面的分析可以看到，最大的頻繁項集為5項集。包括{A:2, C:2, E:2,B:2,F:2}。

　　　　通過上面的流程，相信大家對FP Tree的挖掘頻繁項集的過程也很熟悉了。

5. FP Tree算法歸納

　　　　這里我們對FP Tree算法流程做一個歸納。FP Tree算法包括三步：

　　　　1）掃描數據，得到所有頻繁一項集的的計數。然后刪除支持度低于閾值的項，將1項頻繁集放入項頭表，并按照支持度降序排列。

　　　　2）掃描數據，將讀到的原始數據剔除非頻繁1項集，并按照支持度降序排列。

　　　　3）讀入排序后的數據集，插入FP樹，插入時按照排序后的順序，插入FP樹中，排序靠前的節點是祖先節點，而靠后的是子孫節點。如果有共用的祖先，則對應的公用祖先節點計數加1。插入后，如果有新節點出現，則項頭表對應的節點會通過節點鏈表鏈接上新節點。直到所有的數據都插入到FP樹后，FP樹的建立完成。

　　　　4）從項頭表的底部項依次向上找到項頭表項對應的條件模式基。從條件模式基遞歸挖掘得到項頭表項項的頻繁項集。

　　　　5）如果不限制頻繁項集的項數，則返回步驟4所有的頻繁項集，否則只返回滿足項數要求的頻繁項集。

6. FP tree算法總結

　　　　FP Tree算法改進了Apriori算法的I/O瓶頸，巧妙的利用了樹結構，這讓我們想起了BIRCH聚類，BIRCH聚類也是巧妙的利用了樹結構來提高算法運行速度。利用內存數據結構以空間換時間是常用的提高算法運行時間瓶頸的辦法。

　　　　在實踐中，FP Tree算法是可以用于生產環境的關聯算法，而Apriori算法則做為先驅，起著關聯算法指明燈的作用。除了FP Tree，像GSP，CBA之類的算法都是Apriori派系的。

看完上述內容，你們掌握FP Tree算法原理是什么的方法了嗎？如果還想學到更多技能或想了解更多相關內容，歡迎關注億速云行業資訊頻道，感謝各位的閱讀！