Python非平衡數據問題如何解決

今天小編給大家分享一下Python非平衡數據問題如何解決的相關知識點，內容詳細，邏輯清晰，相信大部分人都還太了解這方面的知識，所以分享這篇文章給大家參考一下，希望大家閱讀完這篇文章后有所收獲，下面我們一起來了解一下吧。

SMOTE算法的介紹

SMOTE算法的基本思想就是對少數類別樣本進行分析和模擬，并將人工模擬的新樣本添加到數據集中，進而使原始數據中的類別不再嚴重失衡。該算法的模擬過程采用了KNN技術，模擬生成新樣本的步驟如下：

• 采樣最鄰近算法，計算出每個少數類樣本的K個近鄰;

• 從K個近鄰中隨機挑選N個樣本進行隨機線性插值;

• 構造新的少數類樣本;

• 將新樣本與原數據合成，產生新的訓練集;

為了使讀者理解SMOTE算法實現新樣本的模擬過程，可以參考下圖和人工新樣本的生成過程：

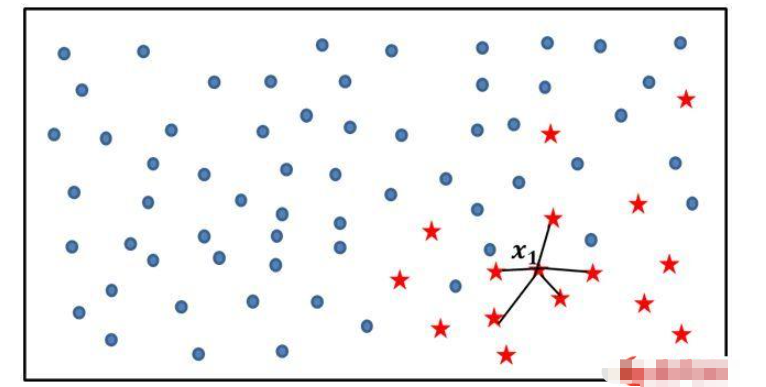
如上圖所示，實心圓點代表的樣本數量要明顯多于五角星代表的樣本點，如果使用SMOTE算法模擬增加少類別的樣本點，則需要經過如下幾個步驟：

• 利用KNN算法，選擇離樣本點x1最近的K個同類樣本點(不妨最近鄰為5);

• 從最近的K個同類樣本點中，隨機挑選M個樣本點(不妨M為2)，M的選擇依賴于最終所希望的平衡率;

• 對于每一個隨機選中的樣本點，構造新的樣本點;新樣本點的構造需要使用下方的公式：

其中，xi表示少數類別中的一個樣本點(如圖中五角星所代表的x1樣本);xj表示從K近鄰中隨機挑選的樣本點j;rand(0,1)表示生成0~1之間的隨機數。

假設圖中樣本點x1的觀測值為(2,3,10,7)，從圖中的5個近鄰中隨機挑選2個樣本點，它們的觀測值分別為(1,1,5,8)和(2,1,7,6)，所以，由此得到的兩個新樣本點為：

• 重復步驟1)、2)和3)，通過迭代少數類別中的每一個樣本xi，最終將原始的少數類別樣本量擴大為理想的比例;

通過SMOTE算法實現過采樣的技術并不是太難，讀者可以根據上面的步驟自定義一個抽樣函數。當然，讀者也可以借助于imblearn模塊，并利用其子模塊over_sampling中的SMOTE“類”實現新樣本的生成。有關該“類”的語法和參數含義如下：

SMOTE(ratio=’auto’, random_state=None, k_neighbors=5, m_neighbors=10,      out_step=0.5, kind=’regular’, svm_estimator=None, n_jobs=1)

• ratio：用于指定重抽樣的比例，如果指定字符型的值，可以是’minority’，表示對少數類別的樣本進行抽樣、’majority’，表示對多數類別的樣本進行抽樣、’not  minority’表示采用欠采樣方法、’all’表示采用過采樣方法，默認為’auto’，等同于’all’和’not  minority’;如果指定字典型的值，其中鍵為各個類別標簽，值為類別下的樣本量;

• random_state：用于指定隨機數生成器的種子，默認為None,表示使用默認的隨機數生成器;

• k_neighbors：指定近鄰個數，默認為5個;

• m_neighbors：指定從近鄰樣本中隨機挑選的樣本個數，默認為10個;

• kind：用于指定SMOTE算法在生成新樣本時所使用的選項，默認為’regular’，表示對少數類別的樣本進行隨機采樣，也可以是’borderline1’、’borderline2’和’svm’;

• svm_estimator：用于指定SVM分類器，默認為sklearn.svm.SVC，該參數的目的是利用支持向量機分類器生成支持向量，然后再生成新的少數類別的樣本;

• n_jobs：用于指定SMOTE算法在過采樣時所需的CPU數量，默認為1表示僅使用1個CPU運行算法，即不使用并行運算功能;

分類算法的應用實戰

本次分享的數據集來源于德國某電信行業的客戶歷史交易數據，該數據集一共包含條4,681記錄，19個變量，其中因變量churn為二元變量，yes表示客戶流失，no表示客戶未流失;剩余的自變量包含客戶的是否訂購國際長途套餐、語音套餐、短信條數、話費、通話次數等。接下來就利用該數據集，探究非平衡數據轉平衡后的效果。

# 導入第三方包 import pandas as pd import numpy as np import matplotlib.pyplot as plt from sklearn import model_selection from sklearn import tree from sklearn import metrics from imblearn.over_sampling import SMOTE # 讀取數據churn = pd.read_excel(r'C:\Users\Administrator\Desktop\Customer_Churn.xlsx') churn.head()

# 中文亂碼的處理 plt.rcParams['font.sans-serif']=['Microsoft YaHei']  # 為確保繪制的餅圖為圓形，需執行如下代碼 plt.axes(aspect = 'equal') # 統計交易是否為欺詐的頻數 counts = churn.churn.value_counts()  # 繪制餅圖 plt.pie(x = counts, # 繪圖數據         labels=pd.Series(counts.index).map({'yes':'流失','no':'未流失'}), # 添加文字標簽         autopct='%.2f%%' # 設置百分比的格式，這里保留一位小數        ) # 顯示圖形 plt.show()

如上圖所示，流失用戶僅占到8.3%，相比于未流失用戶，還是存在比較大的差異的。可以認為兩種類別的客戶是失衡的，如果直接對這樣的數據建模，可能會導致模型的結果不夠準確。不妨先對該數據構建隨機森林模型，看看是否存在偏倚的現象。

原始數據表中的state變量和Area_code變量表示用戶所屬的“州”和地區編碼，直觀上可能不是影響用戶是否流失的重要原因，故將這兩個變量從表中刪除。除此，用戶是否訂購國際長途業務international_plan和語音業務voice_mail_plan，屬于字符型的二元值，它們是不能直接代入模型的，故需要轉換為0-1二元值。

# 數據清洗 # 刪除state變量和area_code變量 churn.drop(labels=['state','area_code'], axis = 1, inplace = True)  # 將二元變量international_plan和voice_mail_plan轉換為0-1啞變量 churn.international_plan = churn.international_plan.map({'no':0,'yes':1}) churn.voice_mail_plan = churn.voice_mail_plan.map({'no':0,'yes':1}) churn.head()

如上表所示，即為清洗后的干凈數據，接下來對該數據集進行拆分，分別構建訓練數據集和測試數據集，并利用訓練數據集構建分類器，測試數據集檢驗分類器：

# 用于建模的所有自變量 predictors = churn.columns[:-1] # 數據拆分為訓練集和測試集 X_train,X_test,y_train,y_test = model_selection.train_test_split(churn[predictors], churn.churn, random_state=12)  # 構建決策樹 dt = tree.DecisionTreeClassifier(n_estimators = 300) dt.fit(X_train,y_train) # 模型在測試集上的預測 pred = dt.predict(X_test)  # 模型的預測準確率 print(metrics.accuracy_score(y_test, pred)) # 模型評估報告 print(metrics.classification_report(y_test, pred))

如上結果所示，決策樹的預測準確率超過93%，其中預測為no的覆蓋率recall為97%，但是預測為yes的覆蓋率recall卻為62%，兩者相差甚遠，說明分類器確實偏向了樣本量多的類別(no)。

# 繪制ROC曲線 # 計算流失用戶的概率值，用于生成ROC曲線的數據 y_score = dt.predict_proba(X_test)[:,1] fpr,tpr,threshold = metrics.roc_curve(y_test.map({'no':0,'yes':1}), y_score)  # 計算AUC的值 roc_auc = metrics.auc(fpr,tpr) # 繪制面積圖 plt.stackplot(fpr, tpr, color='steelblue', alpha = 0.5, edgecolor = 'black') # 添加邊際線 plt.plot(fpr, tpr, color='black', lw = 1) # 添加對角線 plt.plot([0,1],[0,1], color = 'red', linestyle = '--') # 添加文本信息 plt.text(0.5,0.3,'ROC curve (area = %0.3f)' % roc_auc) # 添加x軸與y軸標簽 plt.xlabel('1-Specificity') plt.ylabel('Sensitivity') # 顯示圖形 plt.show()

如上圖所示，ROC曲線下的面積為0.79***UC的值小于0.8，故認為模型不太合理。(通常拿AUC與0.8比較，如果大于0.8，則認為模型合理)。接下來，利用SMOTE算法對數據進行處理：

# 對訓練數據集作平衡處理 over_samples = SMOTE(random_state=1234)  over_samples_X,over_samples_y = over_samples.fit_sample(X_train, y_train)  # 重抽樣前的類別比例 print(y_train.value_counts()/len(y_train)) # 重抽樣后的類別比例 print(pd.Series(over_samples_y).value_counts()/len(over_samples_y))

如上結果所示，對于訓練數據集本身，它的類別比例還是存在較大差異的，但經過SMOTE算法處理后，兩個類別就可以達到1:1的平衡狀態。下面就可以利用這個平衡數據，重新構建決策樹分類器了：

# 基于平衡數據重新構建決策樹模型 dt2 = ensemble.DecisionTreeClassifier(n_estimators = 300) dt2.fit(over_samples_X,over_samples_y) # 模型在測試集上的預測 pred2 =dt2.predict(np.array(X_test))  # 模型的預測準確率 print(metrics.accuracy_score(y_test, pred2)) # 模型評估報告 print(metrics.classification_report(y_test, pred2))

如上結果所示，利用平衡數據重新建模后，模型的準確率同樣很高，為92.6%(相比于原始非平衡數據構建的模型，準確率僅下降1%)，但是預測為yes的覆蓋率提高了10%，達到72%，這就是平衡帶來的好處。

# 計算流失用戶的概率值，用于生成ROC曲線的數據 y_score = rf2.predict_proba(np.array(X_test))[:,1] fpr,tpr,threshold = metrics.roc_curve(y_test.map({'no':0,'yes':1}), y_score) # 計算AUC的值 roc_auc = metrics.auc(fpr,tpr) # 繪制面積圖 plt.stackplot(fpr, tpr, color='steelblue', alpha = 0.5, edgecolor = 'black') # 添加邊際線 plt.plot(fpr, tpr, color='black', lw = 1) # 添加對角線 plt.plot([0,1],[0,1], color = 'red', linestyle = '--') # 添加文本信息 plt.text(0.5,0.3,'ROC curve (area = %0.3f)' % roc_auc) # 添加x軸與y軸標簽 plt.xlabel('1-Specificity') plt.ylabel('Sensitivity')  # 顯示圖形 plt.show()

以上就是“Python非平衡數據問題如何解決”這篇文章的所有內容，感謝各位的閱讀！相信大家閱讀完這篇文章都有很大的收獲，小編每天都會為大家更新不同的知識，如果還想學習更多的知識，請關注億速云行業資訊頻道。