您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
本篇內容主要講解“opencv怎么實現卡爾曼濾波”,感興趣的朋友不妨來看看。本文介紹的方法操作簡單快捷,實用性強。下面就讓小編來帶大家學習“opencv怎么實現卡爾曼濾波”吧!
卡爾曼濾波就是將模型預測的數據和觀測數據進行融合,來過濾掉觀測誤差,進而得到更精確的數據。
以一個小車在平面上走為例子,小車的程序讓它以初速度為V0,加速度為a的運動方式向前運動,但由于各種誤差和原因(比如有風,或者上坡等),我們的小車并不嚴格按照這個模型走,存在噪聲(并且假設高斯分布)。
并且我們不斷的用傳感器來測量小車的位置,但傳感器也存在高斯分布的噪聲。
卡爾曼濾波主要有五大公式,在這個例子的基礎上,我們依次來看一下。
第一個公式:
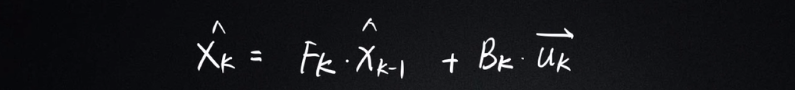
Xk:當前狀態描述矩陣
Fk:狀態轉移矩陣
Bk:控制矩陣
Uk:控制向量
對于小車來說,狀態描述就是它的一維的位置x,以及運動速度v:
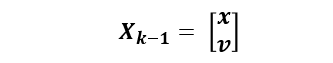
狀態轉移矩陣就是從上一時刻到下一時刻之間的過渡:
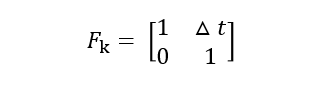
我們將Fk和Xk-1相乘,就可以得到:
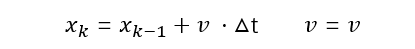
顯而易見,就是在小車勻速運動下的狀態變化了。
但我們的小車是勻加速運動的,我們將加速度視為控制向量Uk,因為加速度是由踩油門啊之類的產生的(姑且這么理解吧)。
因為我們只有一個控制變量,及加速度a,所以
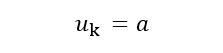
控制矩陣Bk就是將控制向量轉換,將控制變量體現到狀態Xk上:

到此為止,我們用第一個公式推導出了小車從上一個時刻到當前時刻狀態的理想變化。
第二個公式:
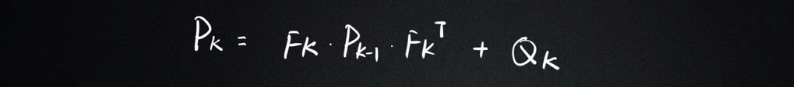
Pk:描述狀態量之間的互相關性,是Xk的協方差矩陣,也就是Cov(Xk)
Fk:狀態轉移矩陣
Qk:外界噪聲的協方差
Pk是Xk的協方差,我們第一個公式更新了狀態向量Xk,第二個公式就是更新Xk的協方差Pk,并加上一個外界噪聲Qk。
因為我們用的是卡爾曼濾波,我們目標對象的狀態都是呈現高斯分布,所以我們有兩個需要關注的變量:均值以及協方差。所以我們需要在更新了Xk,也就包含均值和方差之后,還需要更新協方差,來關注各狀態量之間的關聯程度。
第三個公式:
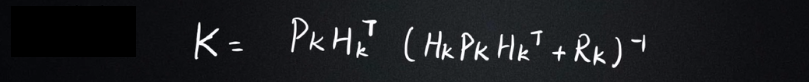
K:卡爾曼增益矩陣
Hk:傳感器數據
Pk :傳感器測量的噪聲的協方差
第三個公式的意義就是求出K,而K是為了在公式四五中使用,單獨拎出來并沒有什么直觀上的意義。
我們知道,卡爾曼濾波就是將傳感器的觀測數據和模型的預測數據相融合,而公式一二做的就是給出模型的預測數據,公式三四五做的就是將預測數據和觀測數據相融合來得到一個新的,更準確的數據。
在這兩者之間有觀測數據的采集這一步,但這不屬于卡爾曼濾波算法要做的。
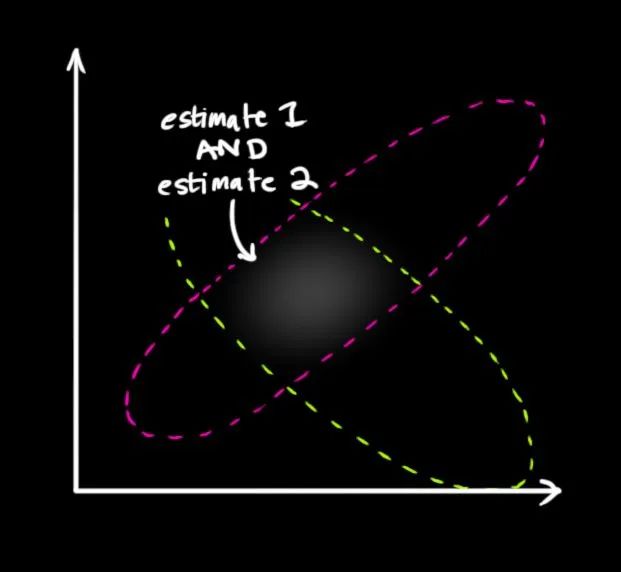
而顯然兩者的重疊部分就是最優的最可能的分布了,如何得到中間這一塊呢?就是將兩個高斯分布相乘。
兩者相乘之后(也就是融合之后),得到的大概如下圖:
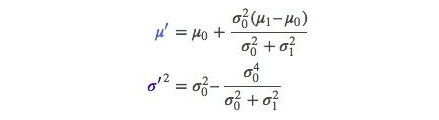
為了簡便,我們用一個k來簡化一下:
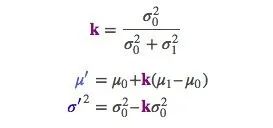
這個k,就是我們公式三求的卡爾曼增益了!(一維情況下)
而后面的兩個公式,就是我們公式四五的一維表達了,不過因為我們實際問題有可能是多維的,所以我們實際的公式用矩陣表示,看著可能更復雜一些。
第四個公式:
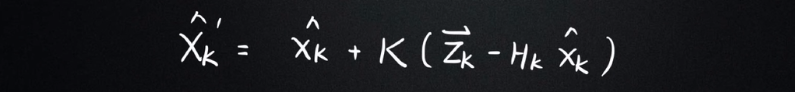
Xk' :數據融合之后的狀態分布
Xk:模型預測的Xk狀態分布
Zk:Xk的均值
HkXk:傳感器觀測數據的均值
第五個公式:

更新狀態描述量的互相關性。
到此,相信大家對“opencv怎么實現卡爾曼濾波”有了更深的了解,不妨來實際操作一番吧!這里是億速云網站,更多相關內容可以進入相關頻道進行查詢,關注我們,繼續學習!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。