matlab python畫二項分布的動態圖方法是什么

本篇內容介紹了“matlab python畫二項分布的動態圖方法是什么”的有關知識，在實際案例的操作過程中，不少人都會遇到這樣的困境，接下來就讓小編帶領大家學習一下如何處理這些情況吧！希望大家仔細閱讀，能夠學有所成！

在數據處理中，matlab和Python是常用的工具，在量化模型中，概率論是一項很重要的基礎，而中心極限定理在概率論中又是一個很重要的理論。

中心極限定理的定義為：

設隨機序列{Xi}獨立同分布，有共同的數學期望u和方差σ^2，部分和由?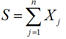?定義，則Sn的標準化

??

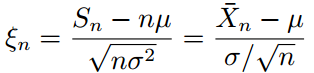依分布收斂到標準正態分布。即對任何x，

??

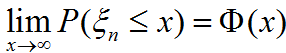這里Φ(x)是標準正態分布的分布函數。

對于二項分布而言，

??

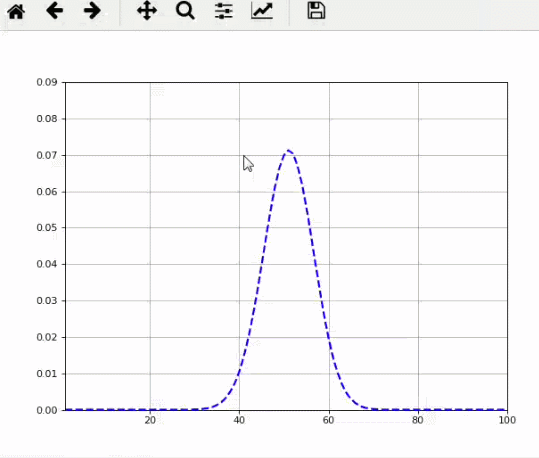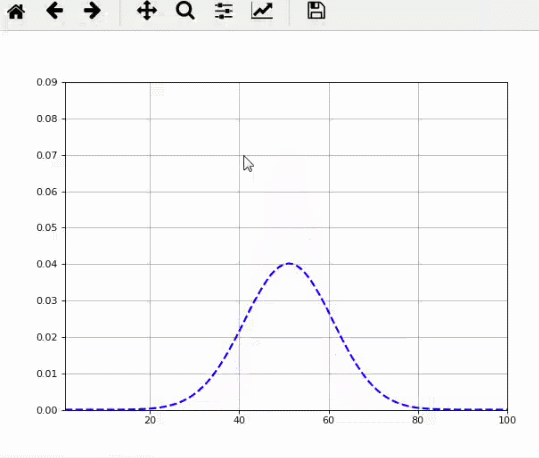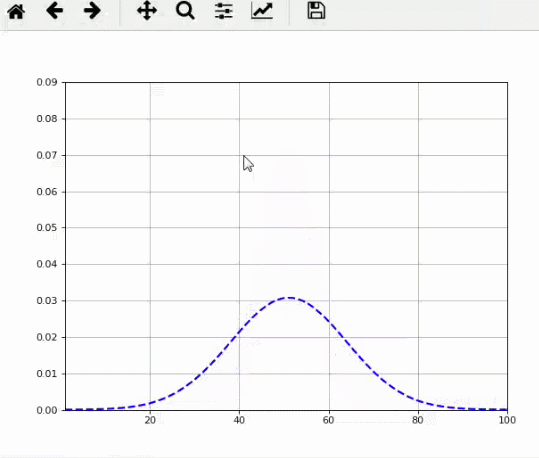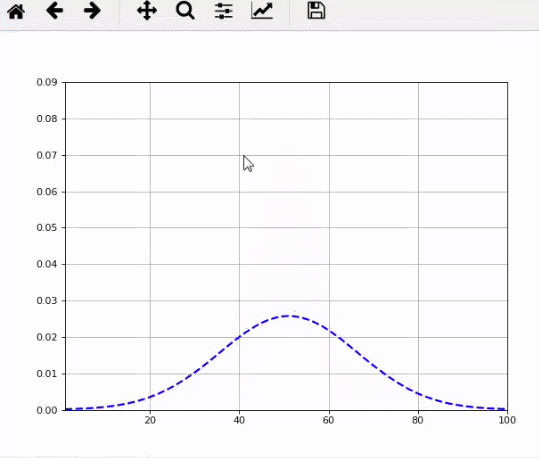
當n→∞時，Sn的分布形狀很像正態分布。

所以，今天我們就來看看，n從小到大時，Sn形狀的變化。

matlab動態圖：

python動態圖：

matlab代碼：

clear all;
close all;
clc;

%% 二項分布
p = 0.6;
n = 1000;
Psn = zeros(1,n+1);
if 1
    h3 =plot(0:n,Psn);
    grid on
    % axis([0 n 0 0.05]);
    axis([1 100 0 0.09]);
    for i=100:10:n
       for k = 0:i
           Psn(k+1) = nchoosek(i,k) * (p^k) * ((1-p)^(i-k));
       end
       set(h3,'XData',1:101,'YData',Psn(floor(i*0.6)-50:floor(i*0.6)+50));
       drawnow
       grid on
       pause(0.01)
    end
end

python代碼：

# -*- coding: utf-8 -*-
"""
-------------------------------------------------
   File Name：    central_limit_theorem1.py
   Description :
   Author :        Z270
   date：         2018/8/30
-------------------------------------------------
   Change Activity:
                   2018/8/30:
-------------------------------------------------
"""
import numpy as np
from scipy.special import comb
import matplotlib.pyplot as plt

p = 0.6
n = 1000
Psn = np.zeros(n+1)

plt.figure(figsize=(8, 6), dpi=80)
# 打開交互模式
plt.ion()
for i in range(100,n+1,10):
    for k in range(i+1):
        Psn[k] = comb(i,k) * (p**k) * ((1-p)**(i-k))
    plt.cla()
    plt.grid(True)
    plt.xlim(1,100)
    plt.ylim(0,0.09)
    plt.plot(range(1,102), Psn[int(np.floor(i*0.6))-50:int(np.floor(i*0.6))+51], 'b--', linewidth = 2.0)
    plt.pause(0.1)
    print(i)
plt.ioff()
plt.show()

“matlab python畫二項分布的動態圖方法是什么”的內容就介紹到這里了，感謝大家的閱讀。如果想了解更多行業相關的知識可以關注億速云網站，小編將為大家輸出更多高質量的實用文章！