您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
今天小編給大家分享一下C++怎么實現不同的路徑的相關知識點,內容詳細,邏輯清晰,相信大部分人都還太了解這方面的知識,所以分享這篇文章給大家參考一下,希望大家閱讀完這篇文章后有所收獲,下面我們一起來了解一下吧。
A robot is located at the top-left corner of a m x n grid (marked "Start" in the diagram below).
The robot can only move either down or right at any point in time. The robot is trying to reach the bottom-right corner of the grid (marked "Finish" in the diagram below).
How many possible unique paths are there?
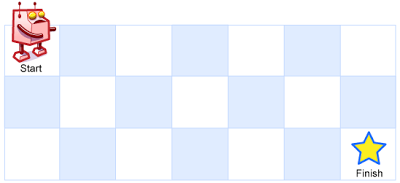
Above is a 7 x 3 grid. How many possible unique paths are there?
Note: m and n will be at most 100.
Example 1:
Input: m = 3, n = 2
Output: 3
Explanation:
From the top-left corner, there are a total of 3 ways to reach the bottom-right corner:
1. Right -> Right -> Down
2. Right -> Down -> Right
3. Down -> Right -> Right
Example 2:
Input: m = 7, n = 3
Output: 28
這道題讓求所有不同的路徑的個數,一開始還真把博主難住了,因為之前好像沒有遇到過這類的問題,所以感覺好像有種無從下手的感覺。在網上找攻略之后才恍然大悟,原來這跟之前那道 Climbing Stairs 很類似,那道題是說可以每次能爬一格或兩格,問到達頂部的所有不同爬法的個數。而這道題是每次可以向下走或者向右走,求到達最右下角的所有不同走法的個數。那么跟爬梯子問題一樣,需要用動態規劃 Dynamic Programming 來解,可以維護一個二維數組 dp,其中 dp[i][j] 表示到當前位置不同的走法的個數,然后可以得到狀態轉移方程為: dp[i][j] = dp[i - 1][j] + dp[i][j - 1],這里為了節省空間,使用一維數組 dp,一行一行的刷新也可以,代碼如下:
解法一:
class Solution {
public:
int uniquePaths(int m, int n) {
vector<int> dp(n, 1);
for (int i = 1; i < m; ++i) {
for (int j = 1; j < n; ++j) {
dp[j] += dp[j - 1];
}
}
return dp[n - 1];
}
};這道題其實還有另一種很數學的解法,實際相當于機器人總共走了 m + n - 2步,其中 m - 1 步向右走,n - 1 步向下走,那么總共不同的方法個數就相當于在步數里面 m - 1 和 n - 1 中較小的那個數的取法,實際上是一道組合數的問題,寫出代碼如下:
解法二:
class Solution {
public:
int uniquePaths(int m, int n) {
double num = 1, denom = 1;
int small = m > n ? n : m;
for (int i = 1; i <= small - 1; ++i) {
num *= m + n - 1 - i;
denom *= i;
}
return (int)(num / denom);
}
};以上就是“C++怎么實現不同的路徑”這篇文章的所有內容,感謝各位的閱讀!相信大家閱讀完這篇文章都有很大的收獲,小編每天都會為大家更新不同的知識,如果還想學習更多的知識,請關注億速云行業資訊頻道。
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。