您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
這篇文章給大家分享的是有關web開發中拓撲排序是什么的內容。小編覺得挺實用的,因此分享給大家做個參考,一起跟隨小編過來看看吧。
Topological sort 又稱 Topological order,這個名字有點迷惑性,因為拓撲排序并不是一個純粹的排序算法,它只是針對某一類圖,找到一個可以執行的線性順序。
這個算法聽起來高大上,如今的面試也很愛考,比如當時我在面我司時有整整一輪是基于拓撲排序的設計。
但它其實是一個很好理解的算法,跟著我的思路,讓你再也不會忘記她。
剛剛我們提到,拓撲排序只是針對特定的一類圖,那么是針對哪類圖的呢?
答:Directed acyclic graph (DAG),有向無環圖。即:
這個圖的邊必須是有方向的;
圖內無環。
那么什么是方向呢?
比如微信好友就是有向的,你加了他好友他可能把你刪了你卻不知道。。。那這個朋友關系就是單向的。。
什么是環?環是和方向有關的,從一個點出發能回到自己,這是環。
所以下圖左邊不是環,右邊是。
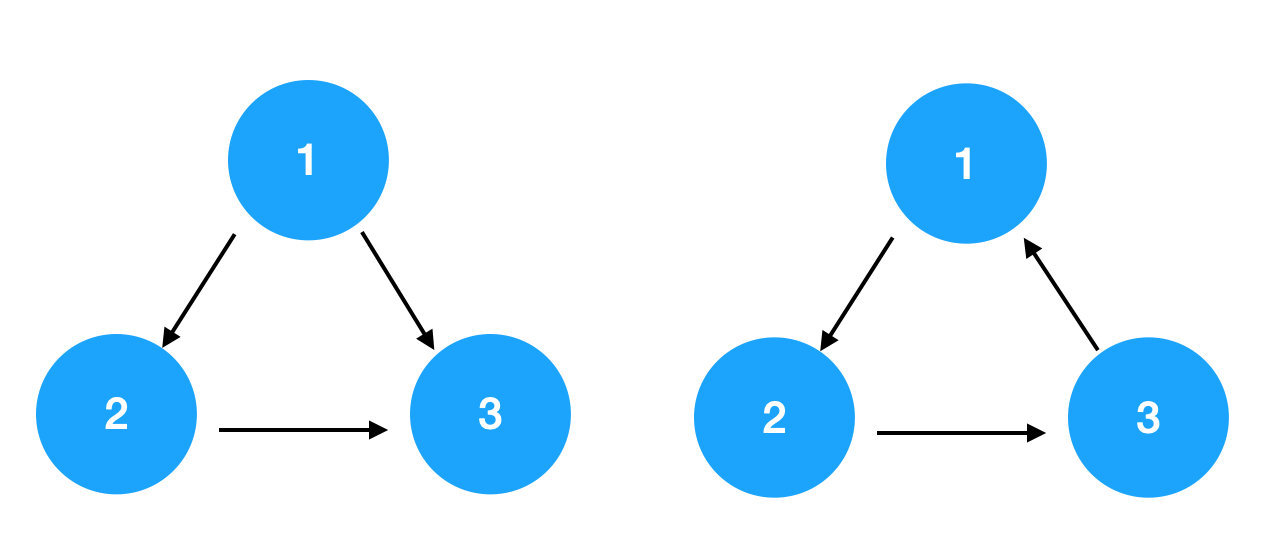
那么如果一個圖里有環,比如右圖,想執行 1 就要先執行 3,想執行 3 就要先執行 2,想執行 2 就要先執行 1,這成了個死循環,無法找到正確的打開方式,所以找不到它的一個拓撲序。
如果這個圖不是 DAG,那么它是沒有拓撲序的;
如果是 DAG,那么它至少有一個拓撲序;
反之,如果它存在一個拓撲序,那么這個圖必定是 DGA.
所以這是一個充分必要條件。

那么這么一個圖的「拓撲序」是什么意思呢?
我們借用百度百科的這個課程表來說明。
| 課程代號 | 課程名稱 | 先修課程 |
|---|---|---|
| C1 | 高等數學 | 無 |
| C2 | 程序設計基礎 | 無 |
| C3 | 離散數學 | C1, C2 |
| C4 | 數據結構 | C3, C5 |
| C5 | 算法語言 | C2 |
| C6 | 編譯技術 | C4, C5 |
| C7 | 操作系統 | C4, C9 |
| C8 | 普通物理 | C1 |
| C9 | 計算機原理 | C8 |
這里有 9 門課程,有些課程是有先修課程的要求的,就是你要先學了「最右側這一欄要求的這個課」才能再去選「高階」的課程。
那么這個例子中拓撲排序的意思就是:
就是求解一種可行的順序,能夠讓我把所有課都學了。
那怎么做呢?
首先我們可以用圖來描述它,
圖的兩個要素是頂點和邊,
那么在這里:
頂點:每門課
邊:起點的課程是終點的課程的先修課
畫出來長這個樣:
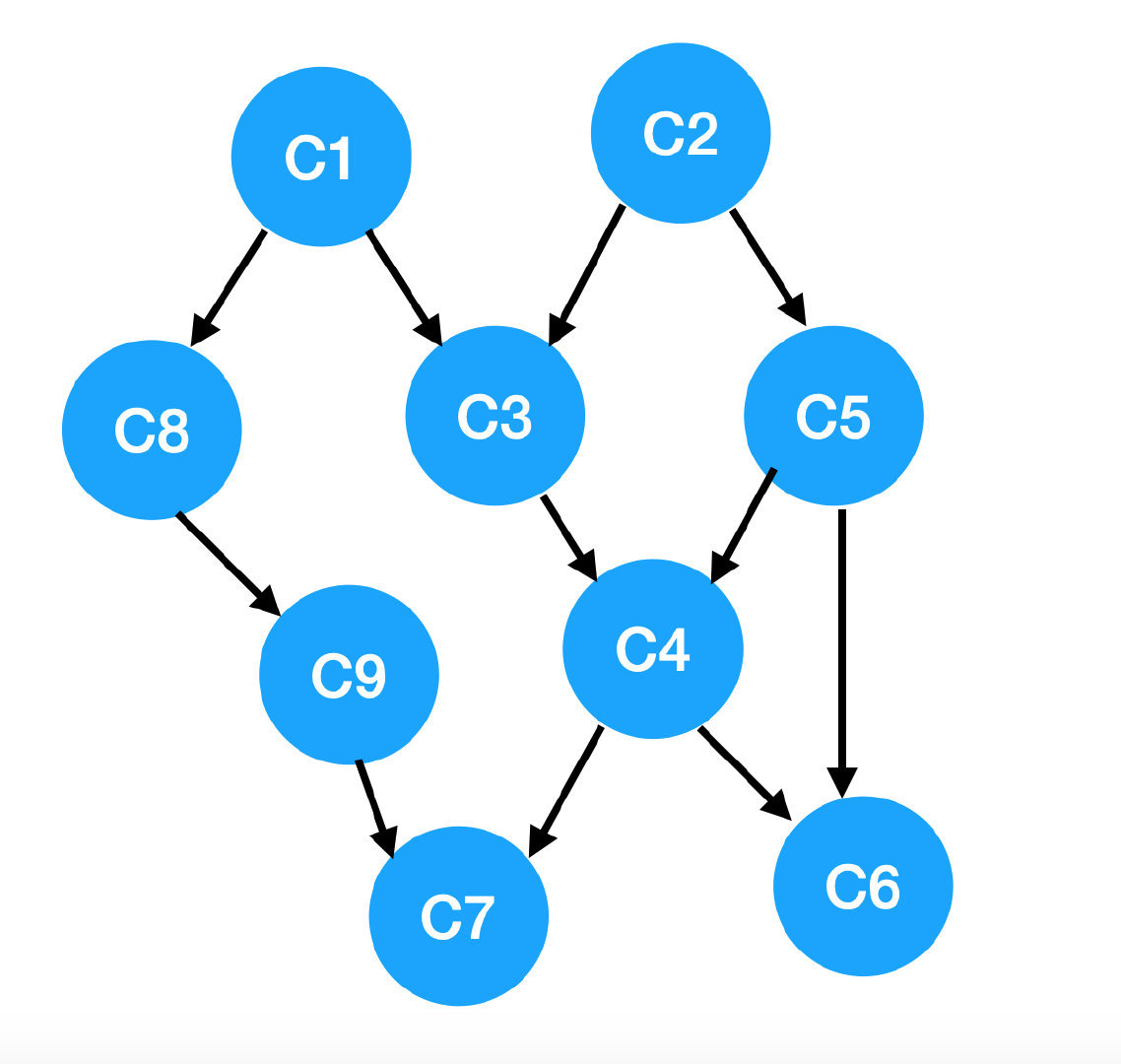
這種圖叫 AOV (Activity On Vertex) 網絡,在這種圖里:
頂點:表示活動;
邊:表示活動間的先后關系
所以一個 AOV 網應該是一個 DAG,即有向無環圖,否則某些活動會無法進行。
<span >那么所有活動可以排成一個可行線性序列,這個序列就是拓撲序列。
那么這個序列的實際意義是:
按照這個順序,在每個項目開始時,能夠保證它的前驅活動都已完成,從而使整個工程順利進行。
回到我們這個例子中:
我們一眼可以看出來要先學 C1, C2,因為這兩門課沒有任何要求嘛,大一的時候就學唄;
大二就可以學第二行的 C3, C5, C8 了,因為這三門課的先修課程就是 C1, C2,我們都學完了;
大三可以學第三行的 C4, C9;
最后一年選剩下的 C6, C7。
這樣,我們就把所有課程學完了,也就得到了這個圖的一個拓撲排序。
注意,有時候拓撲序并不是唯一的,比如在這個例子中,先學 C1 再學 C2,和先 C2 后 C1 都行,都是這個圖的正確的拓撲序,但這是兩個順序了。
所以面試的時候要問下面試官,是要求解任意解,還是列出所有解。
我們總結一下,
在這個圖里的邊表示的是一種依賴關系,如果要修下一門課,就要先把前一門課修了。
這和打游戲里一樣一樣的嘛,要拿到一個道具,就要先做 A 任務,再完成 B 任務,最終終于能到達目的地了。
在上面的圖里,大家很容易就看出來了它的拓撲序,但當工程越來越龐大時,依賴關系也會變得錯綜復雜,那就需要用一種系統性的方式方法來求解了。
那么我們回想一下剛剛自己找拓撲序的過程,為什么我們先看上了 C1, C2?
因為它們沒有依賴別人啊,
也就是它的入度為 0.
入度:頂點的入度是指「指向該頂點的邊」的數量;
出度:頂點的出度是指該頂點指向其他點的邊的數量。
所以我們先執行入度為 0 的那些點,
那也就是要記錄每個頂點的入度。
因為只有當它的 入度 = 0 的時候,我們才能執行它。
在剛才的例子里,最開始 C1, C2 的入度就是 0,所以我們可以先執行這兩個。
那在這個算法里第一步就是得到每個頂點的入度。
我們可以用一個 HashMap 來存放這個信息,或者用一個數組會更精巧。
在文中為了方便展示,我就用表格了:
| C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | C9 | |
|---|---|---|---|---|---|---|---|---|---|
| 入度 | 0 | 0 | 2 | 2 | 1 | 2 | 2 | 1 | 1 |
拿到了這個之后,就可以執行入度為 0 的這些點了,也就是 C1, C2.
那我們把可以被執行的這些點,放入一個待執行的容器里,這樣之后我們一個個的從這個容器里取頂點就好了。
至于這個容器究竟選哪種數據結構,這取決于我們需要做哪些操作,再看哪種數據結構可以為之服務。
那么首先可以把[C1, C2]放入容器中,
然后想想我們需要哪些操作吧!
我們最常做的操作無非就是把點放進來,把點拿出去執行了,也就是需要一個 offer 和 poll 操作比較高效的數據結構,那么 queue 就夠用了。
(其他的也行,放進來這個容器里的頂點的地位都是一樣的,都是可以執行的,和進來的順序無關,但何必非得給自己找麻煩呢?一個常規順序的簡簡單單的 queue 就夠用了。)
然后就需要把某些點拿出去執行了。
【劃重點】當我們把 C1 拿出來執行,那這意味這什么?
<span >答:意味著「以 C1 為頂點」的「指向其他點」的「邊」都消失了,也就是 C1 的出度變成了 0.
如下圖,也就是這兩條邊可以消失了。
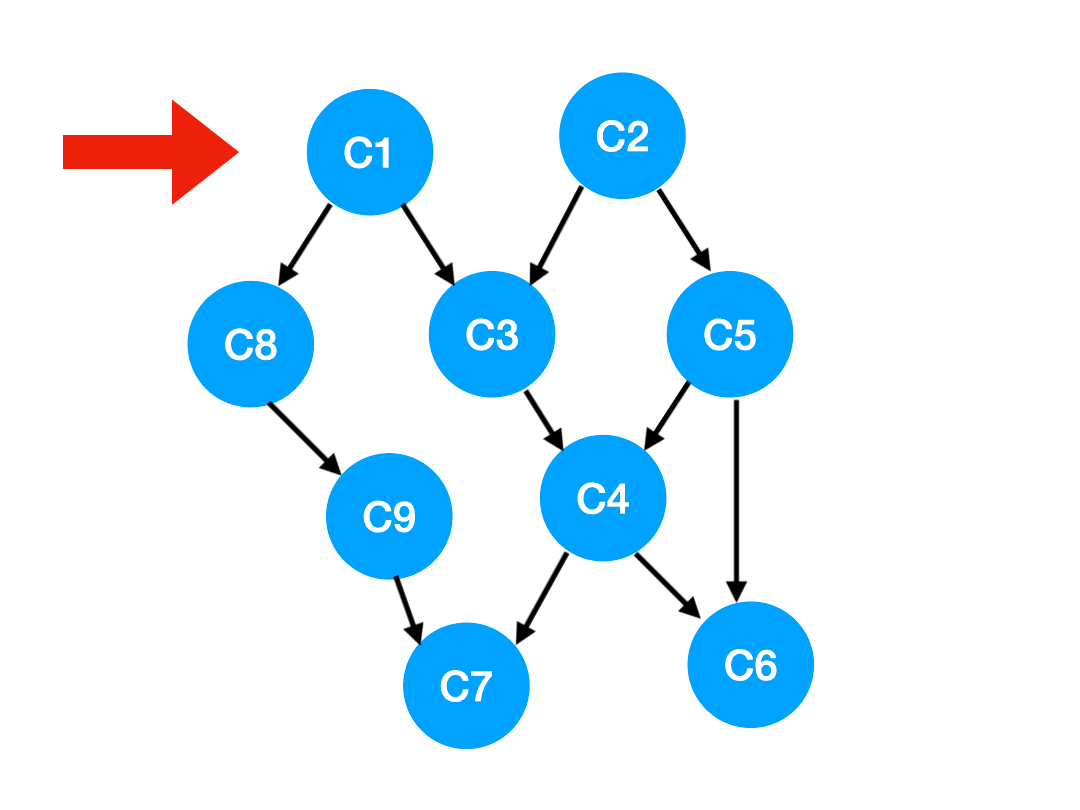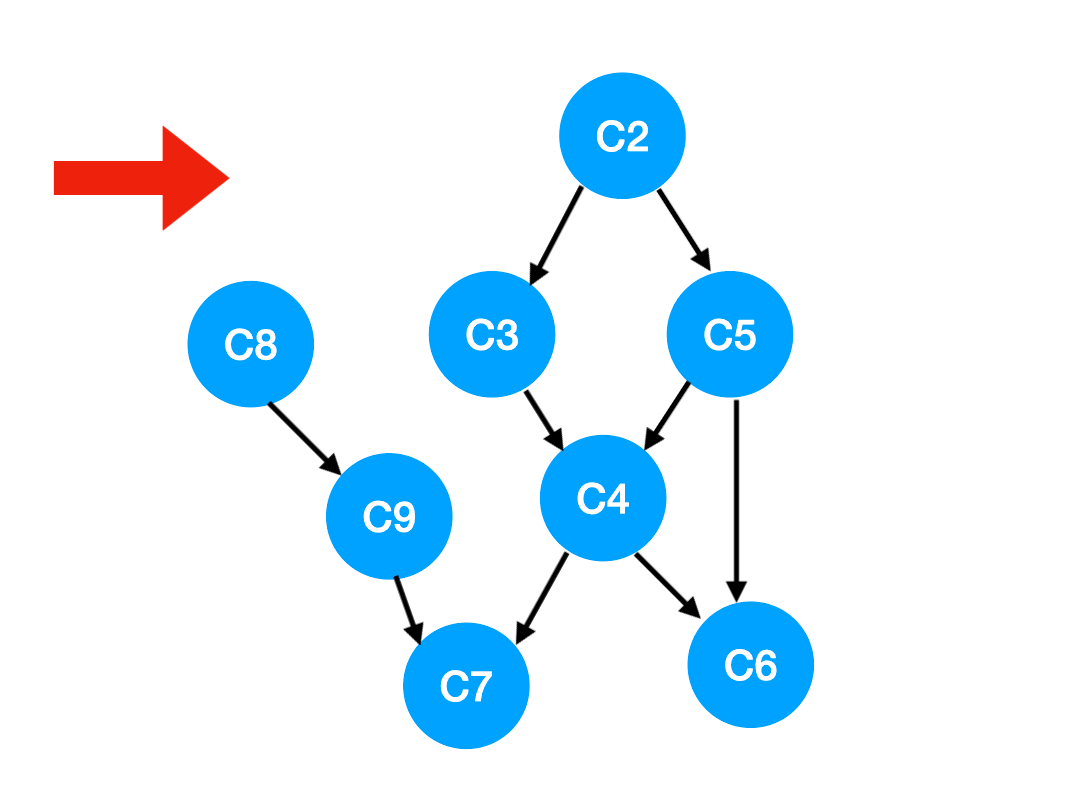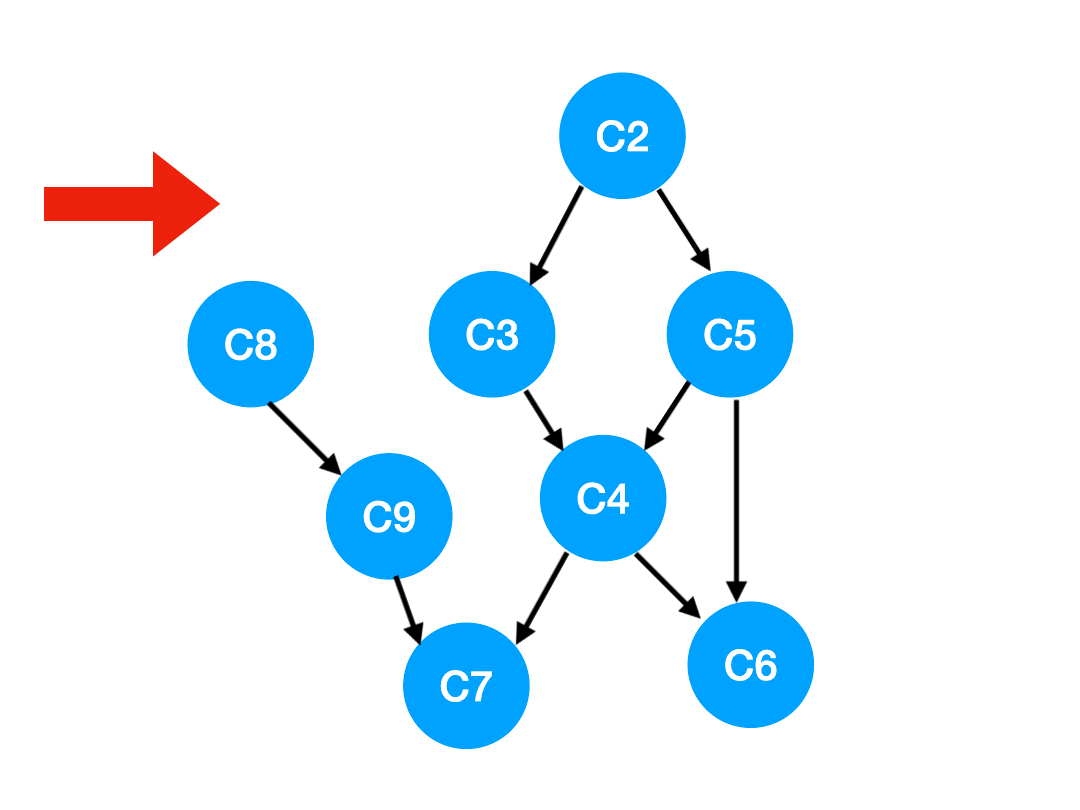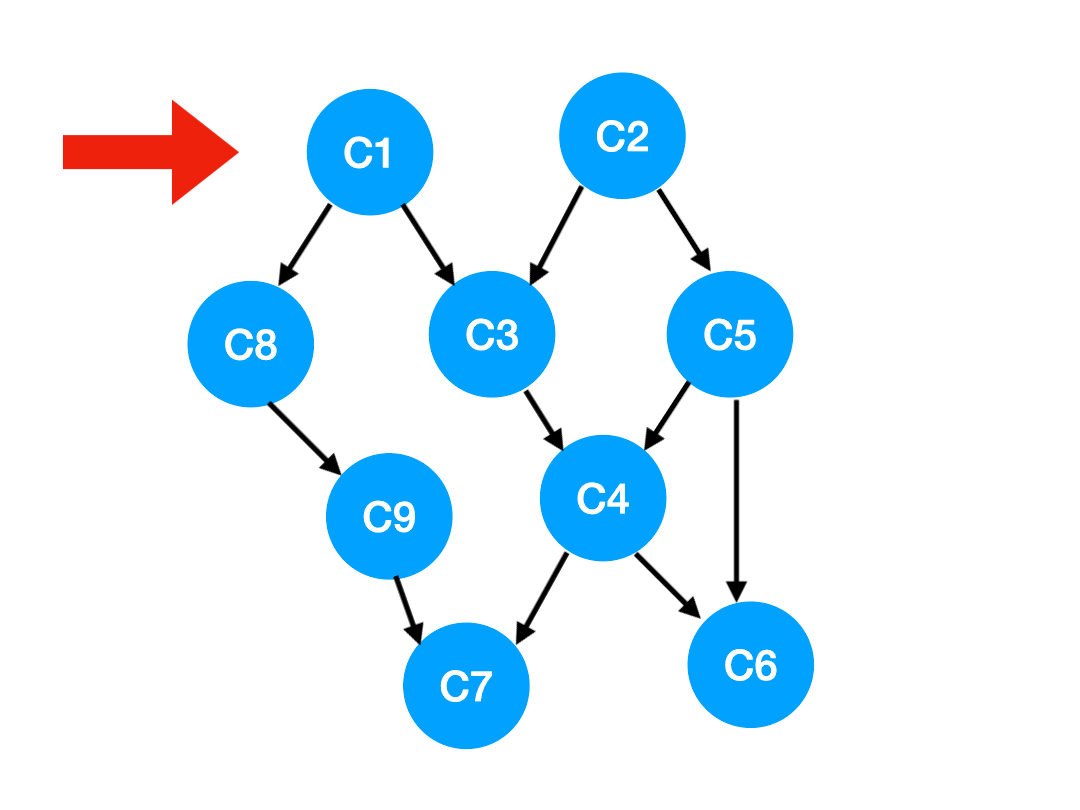
那么此時我們就可以更新 C1 所指向的那些點也就是 C3 和 C8 的 入度 了,更新后的數組如下:
| C3 | C4 | C5 | C6 | C7 | C8 | C9 | |
|---|---|---|---|---|---|---|---|
| 入度 | 1 | 2 | 1 | 2 | 2 | <span >0 | 1 |
<span >那我們這里看到很關鍵的一步,C8 的入度變成了 0!
也就意味著 C8 此時沒有了任何依賴,可以放到我們的 queue 里等待執行了。
此時我們的 queue 里就是:[C2, C8].
下一個我們再執行 C2,
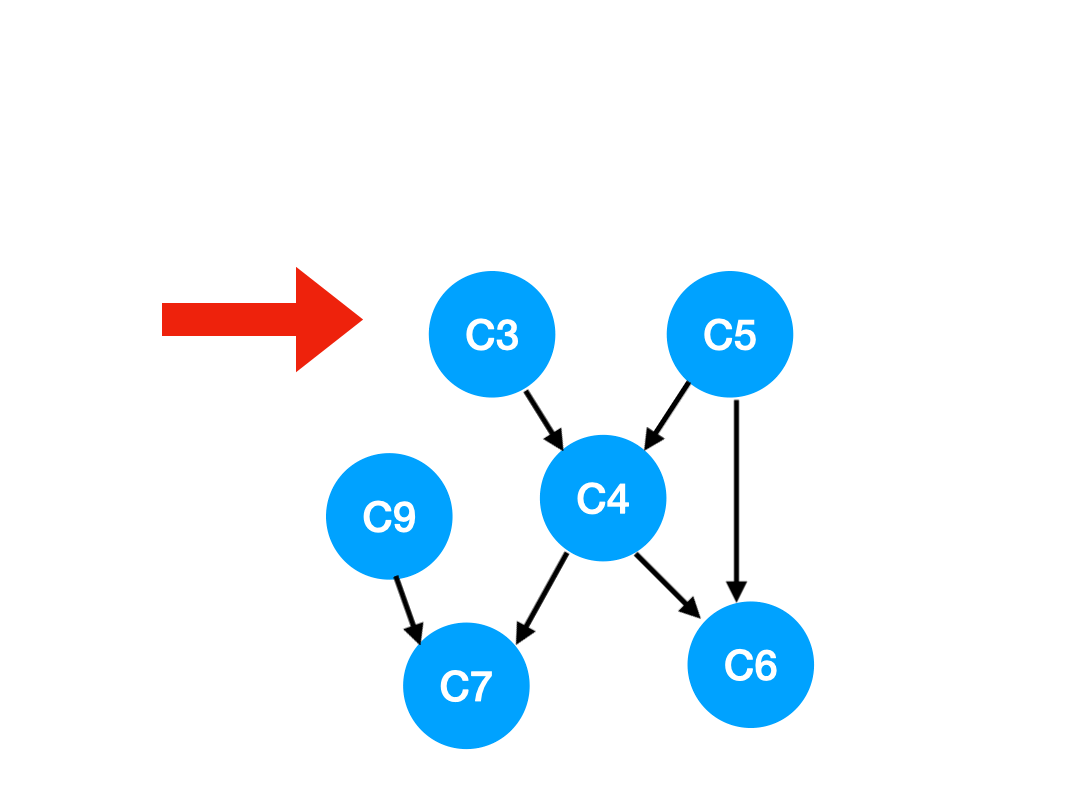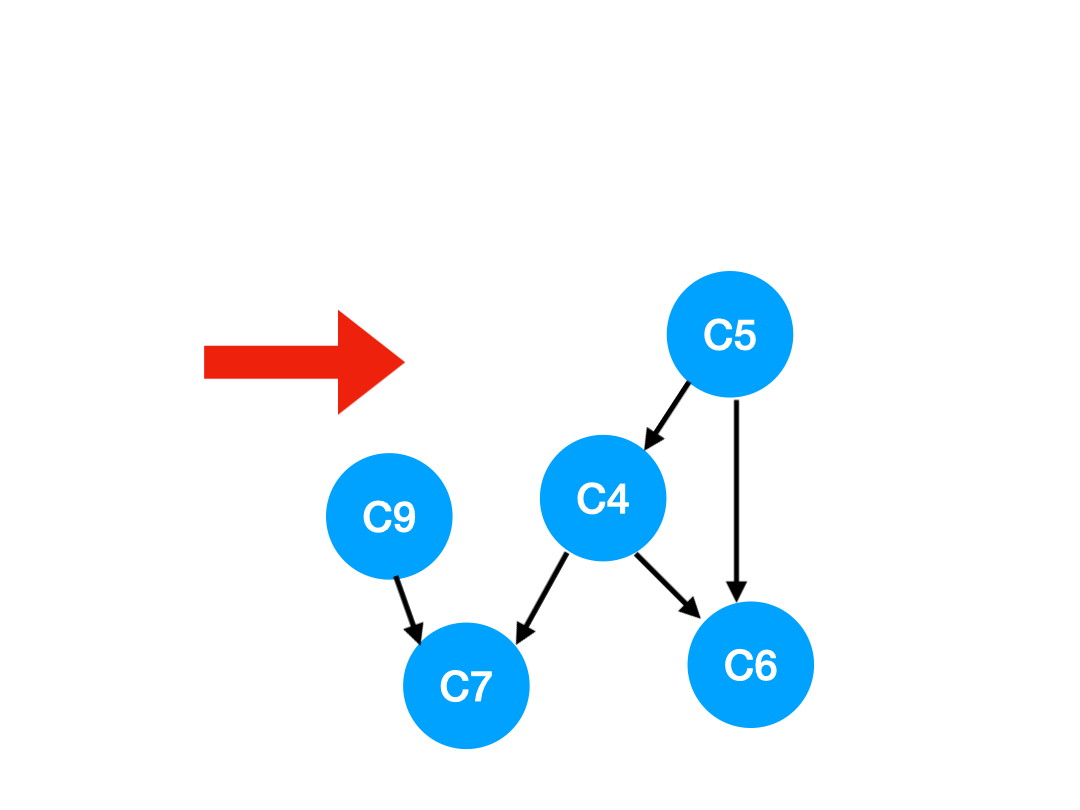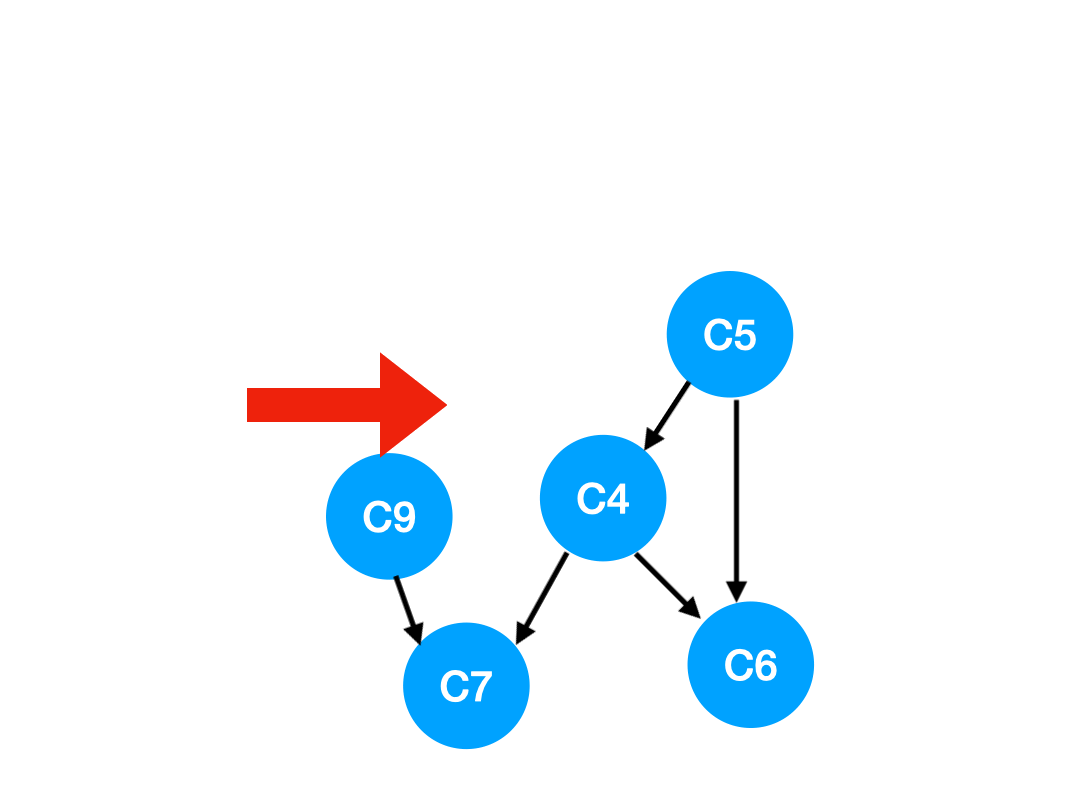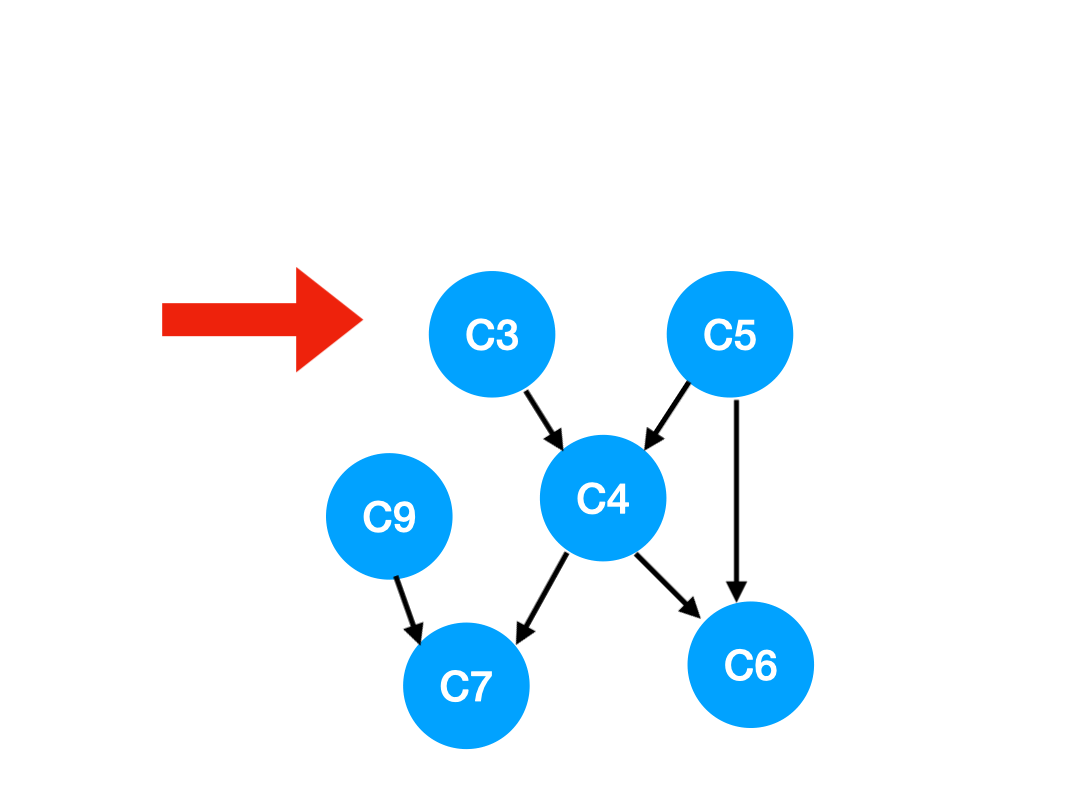
那么 C2 所指向的 C3, C5 的 入度-1,
更新表格:
| C3 | C4 | C5 | C6 | C7 | C9 | |
|---|---|---|---|---|---|---|
| 入度 | <span >0 | 2 | <span >0 | 2 | 2 | 1 |
也就是 C3 和 C5 都沒有了任何束縛,可以放進 queue 里執行了。
queue 此時變成:[C8, C3, C5]
那么下一步我們執行 C8,
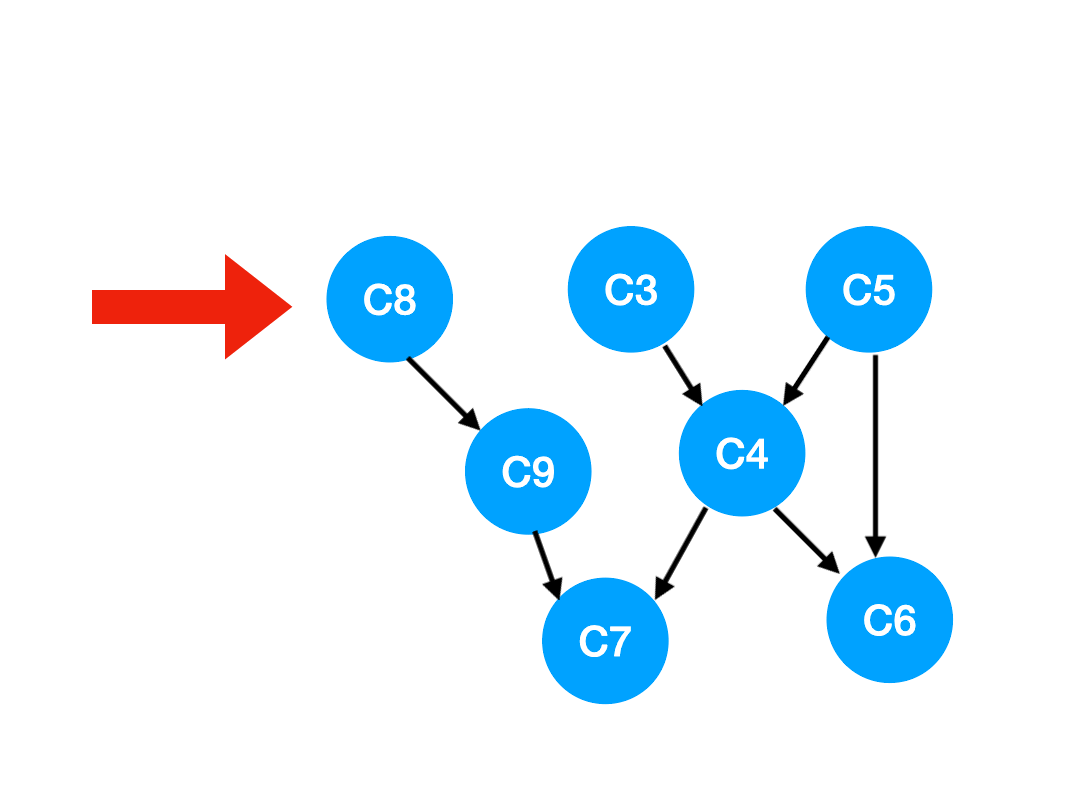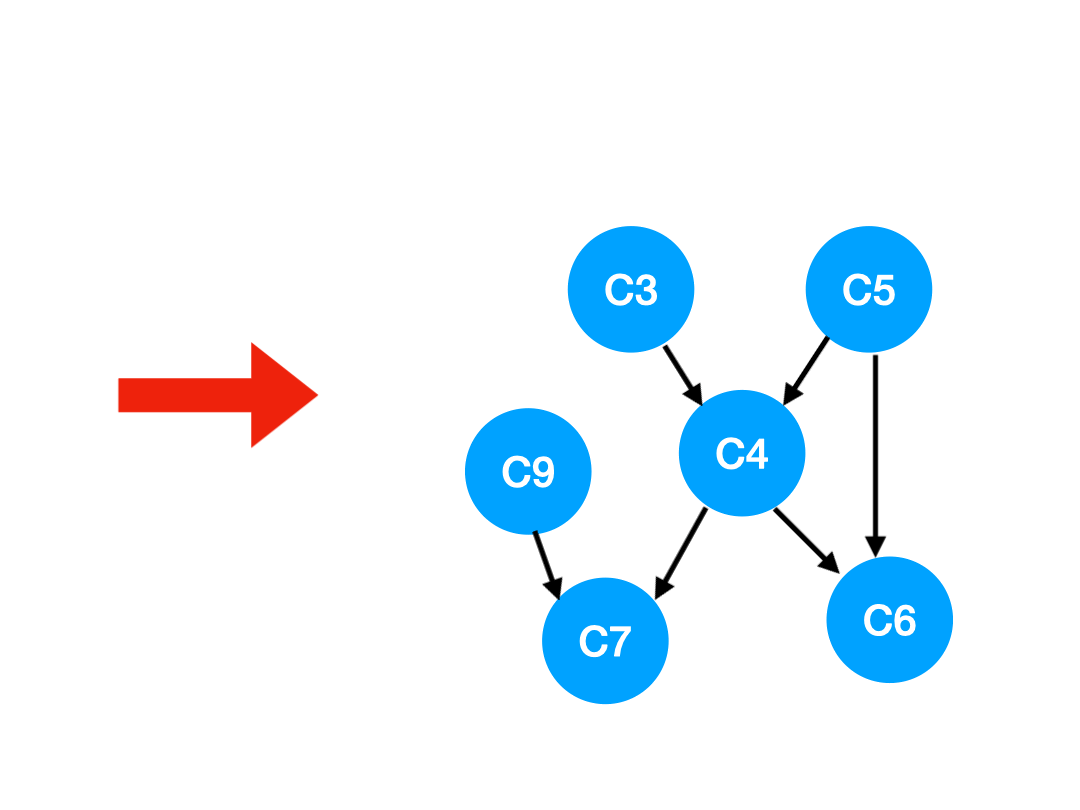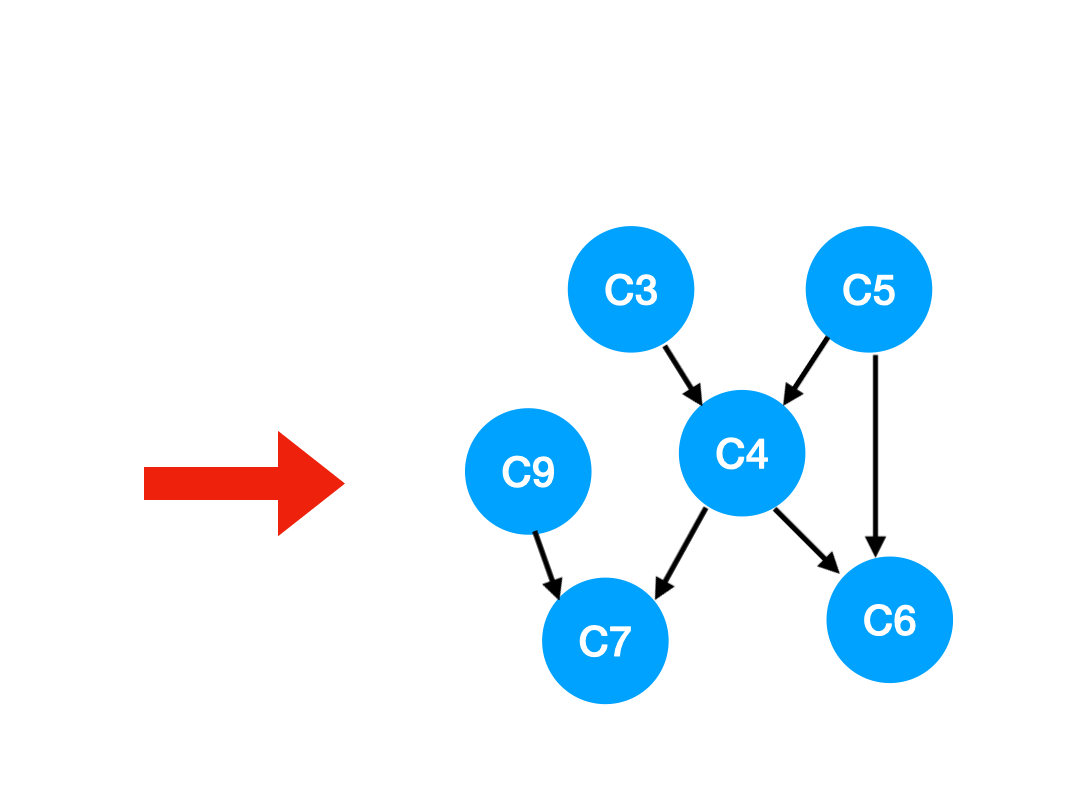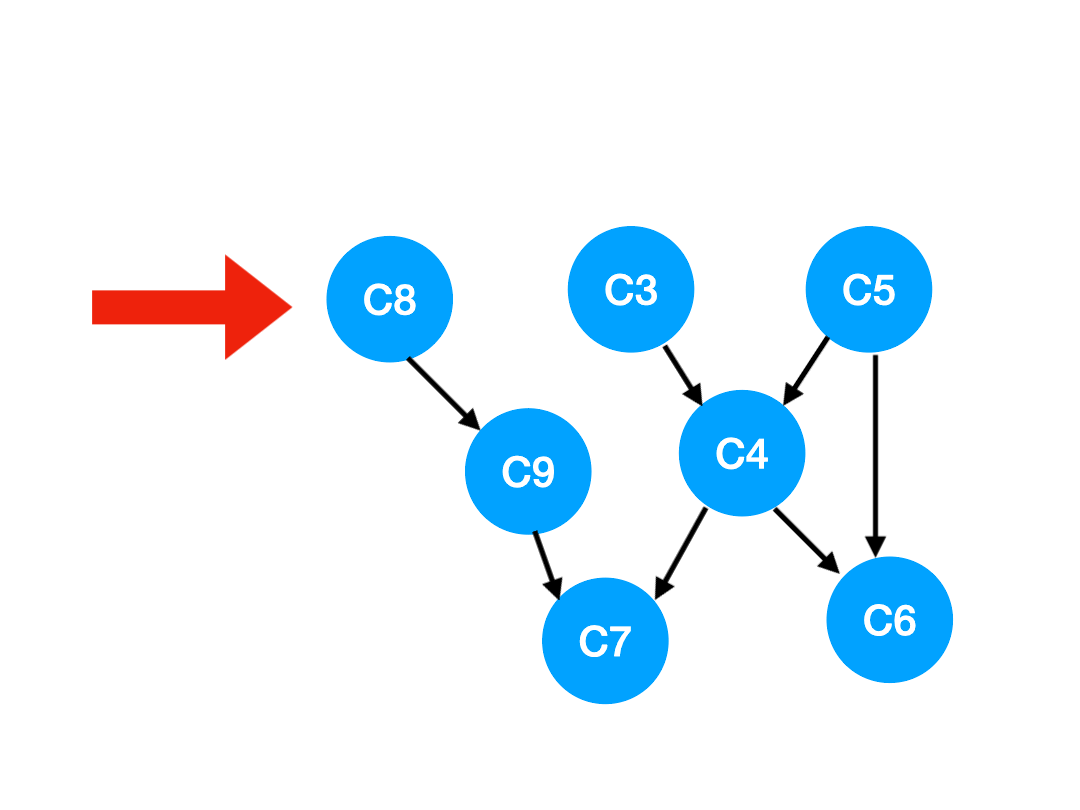
相應的 C8 所指的 C9 的入度-1.
更新表格:
| C4 | C6 | C7 | C9 | |
|---|---|---|---|---|
| 入度 | 2 | 2 | 2 | <span >0 |
那么 C9 沒有了任何要求,可以放進 queue 里執行了。
queue 此時變成:[C3, C5, C9]
接下來執行 C3,
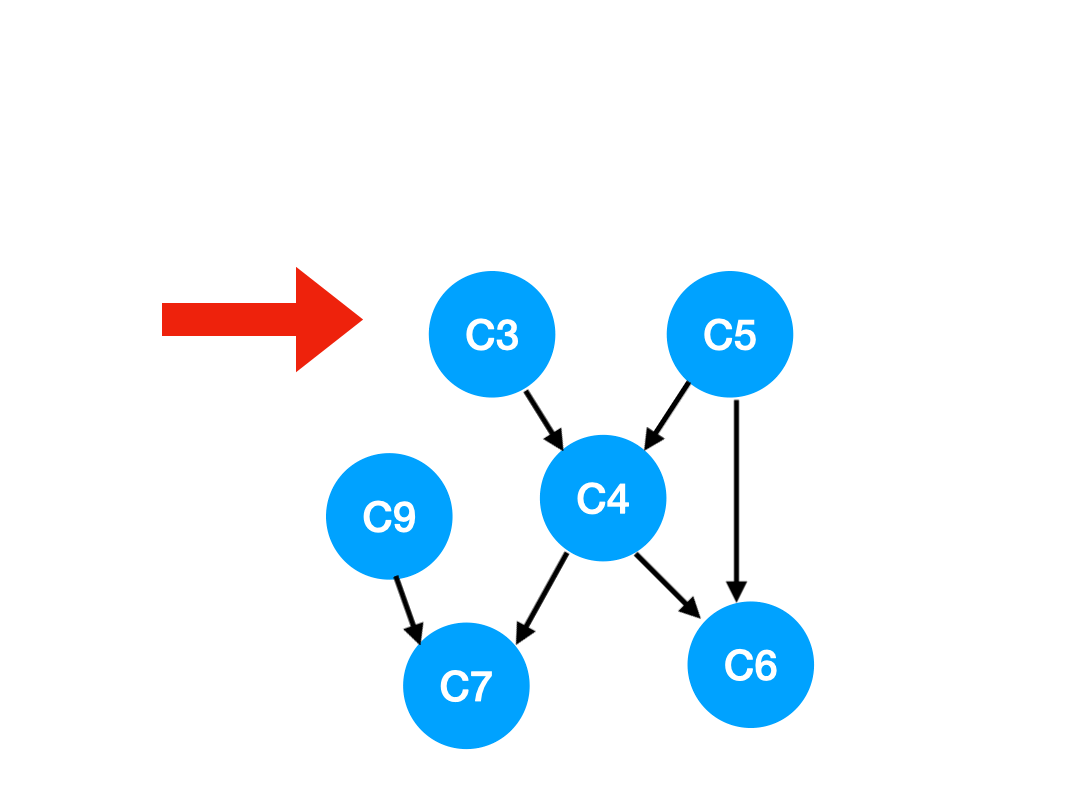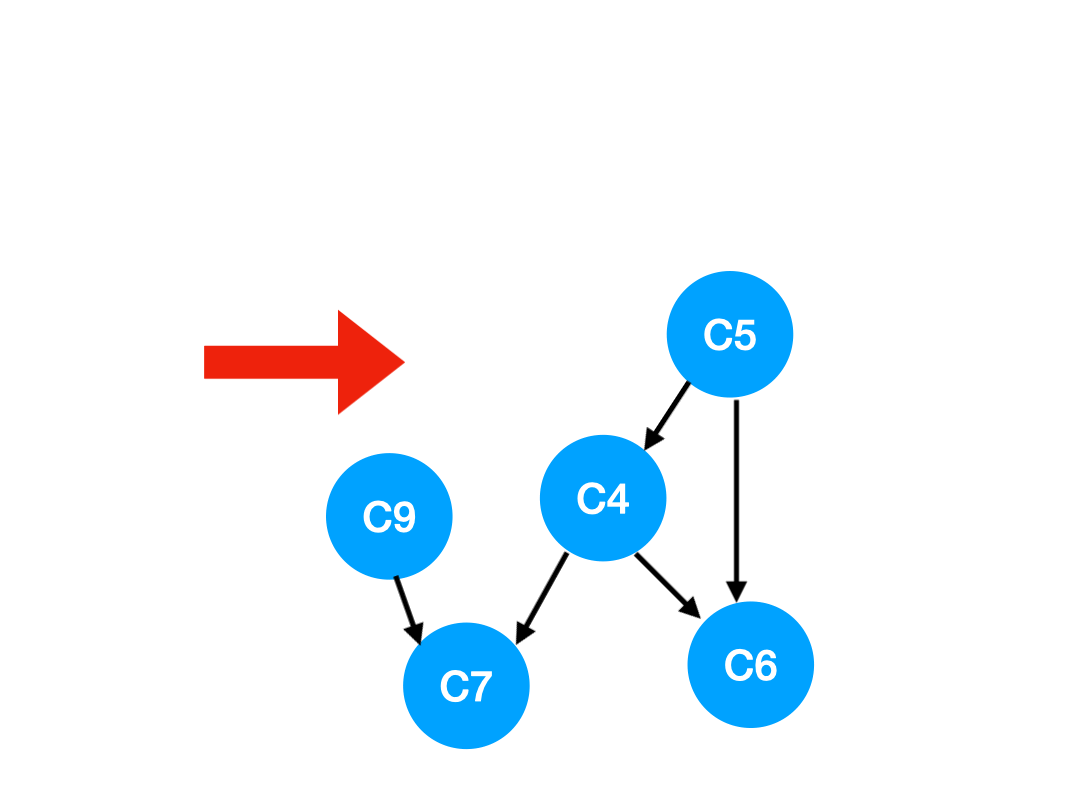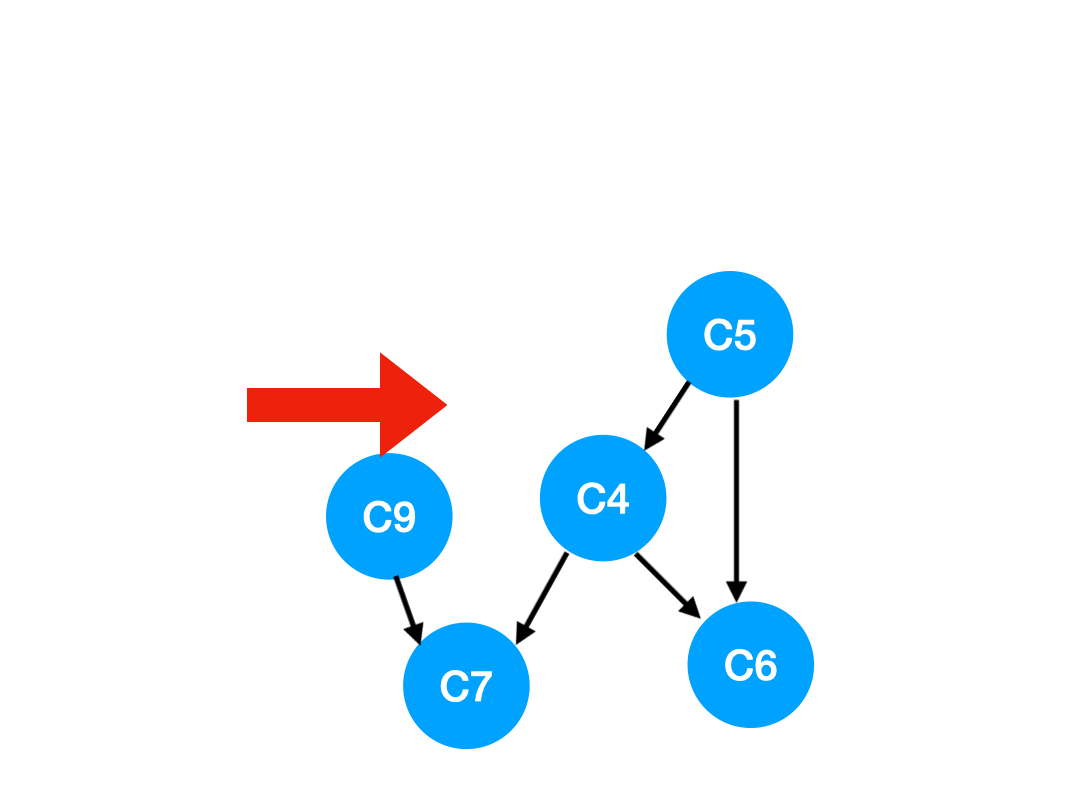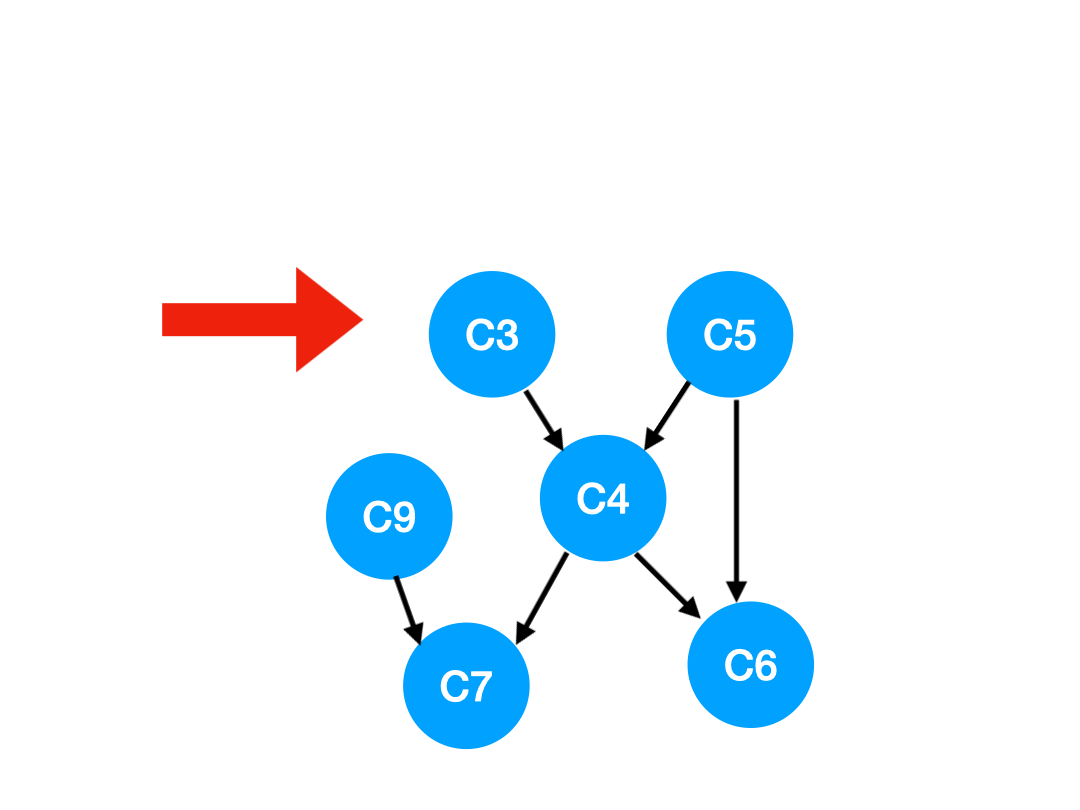
相應的 C3 所指的 C4 的入度-1.
更新表格:
| C4 | C6 | C7 | |
|---|---|---|---|
| 入度 | <span >1 | 2 | 2 |
<span >但是 C4 的入度并沒有變成 0,所以這一步沒有任何點可以加入 queue.
queue 此時變成 [C5, C9]
再執行 C5,
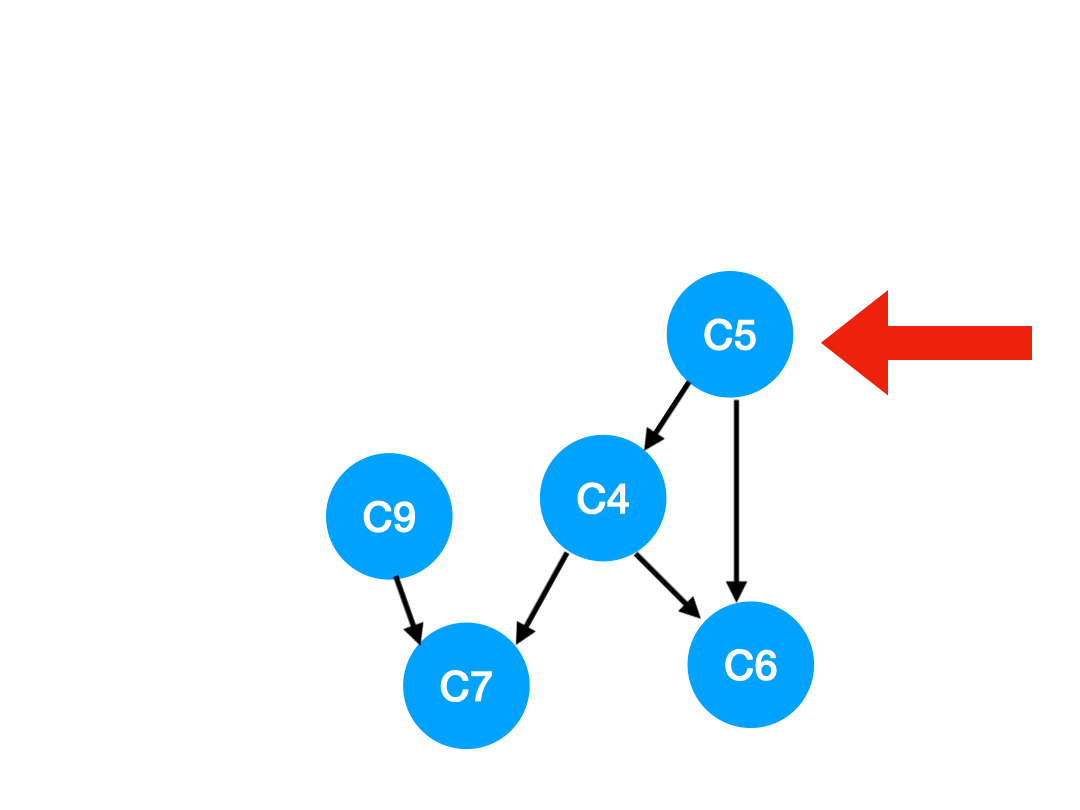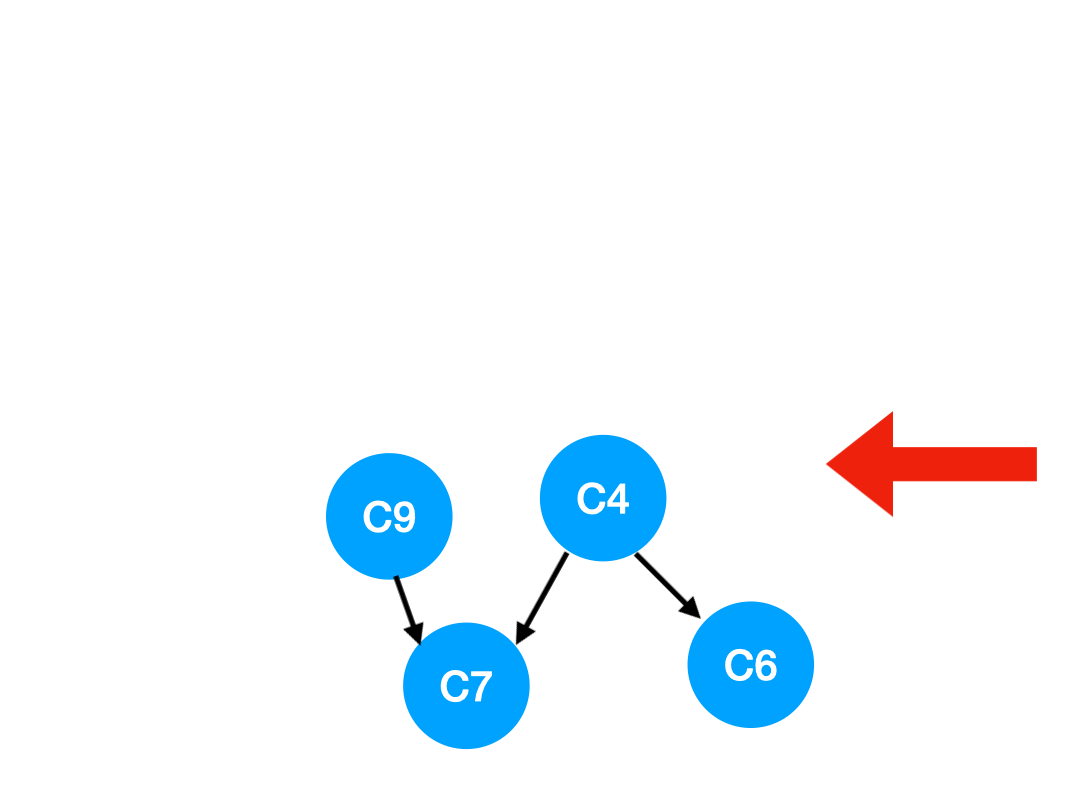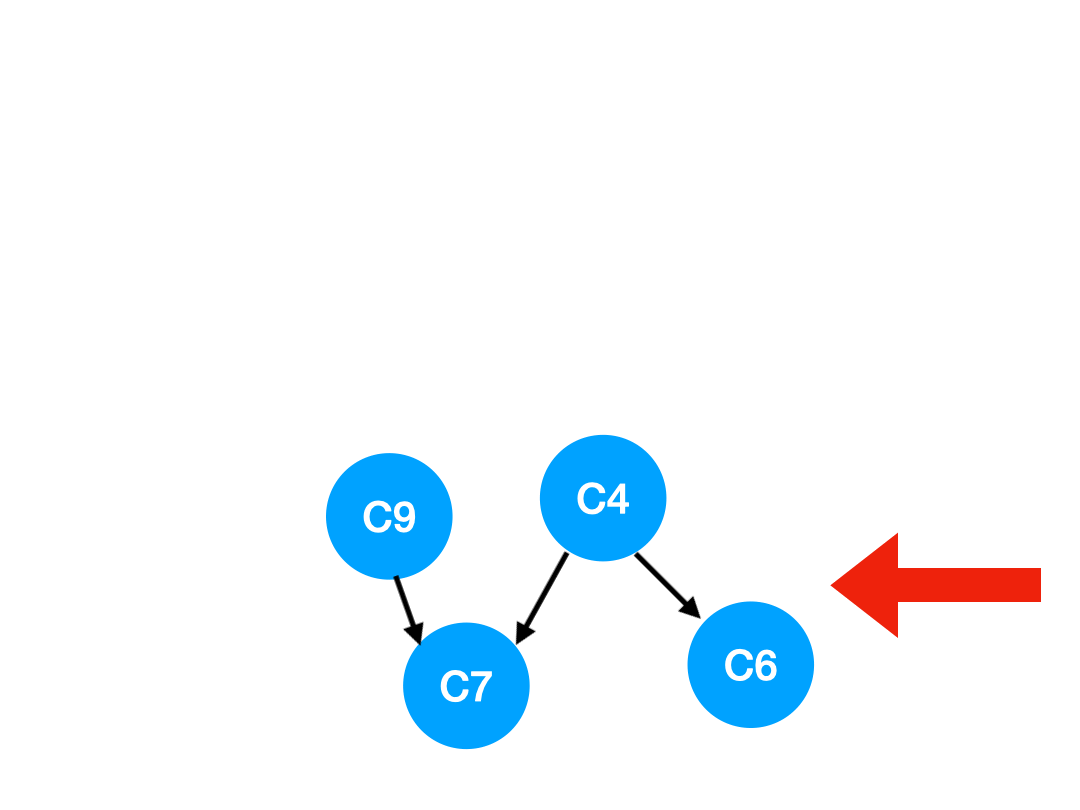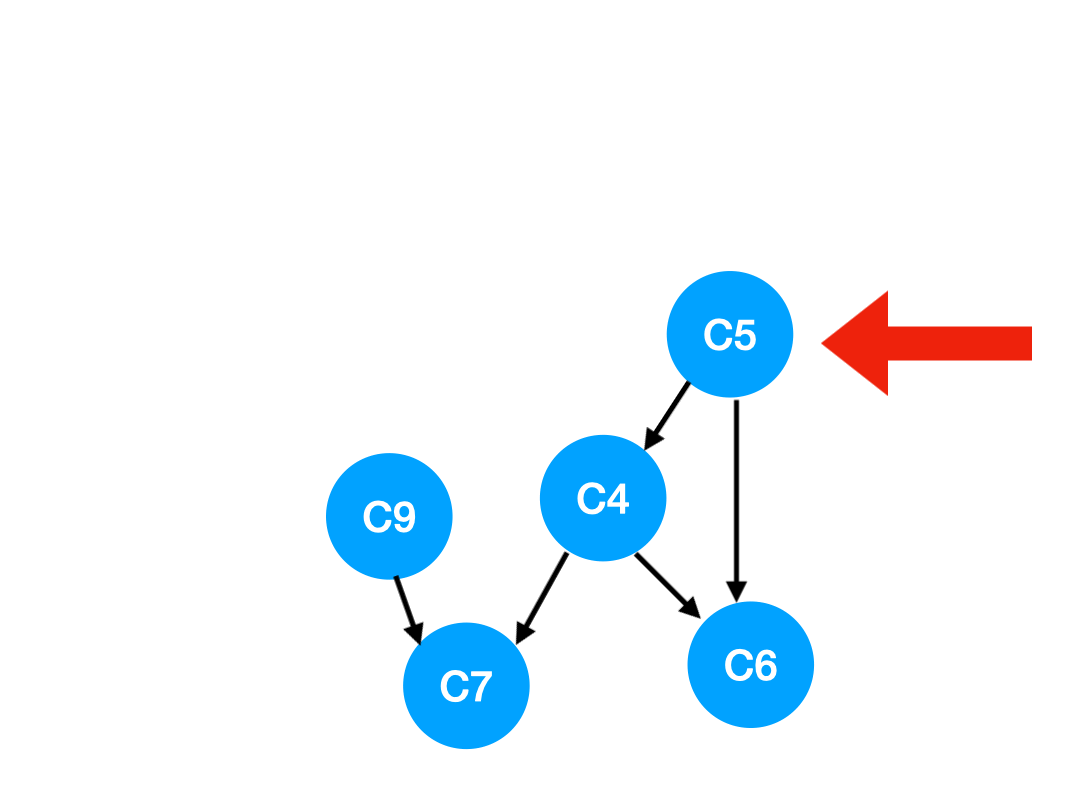
那么 C5 所指的 C4 和 C6 的入度- 1.
更新表格:
| C4 | C6 | C7 | |
|---|---|---|---|
| 入度 | <span >0 | <span >1 | 2 |
這里 C4 的依賴全都消失啦,那么可以把 C4 放進 queue 里了:
queue = [C9, C4]
然后執行 C9,
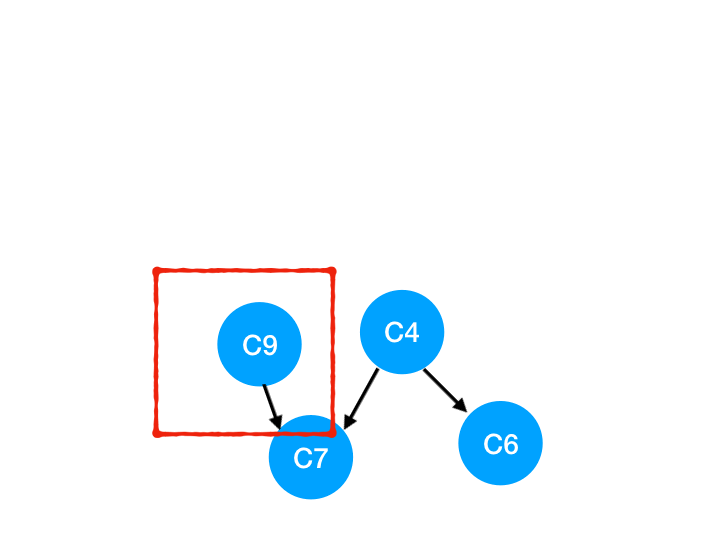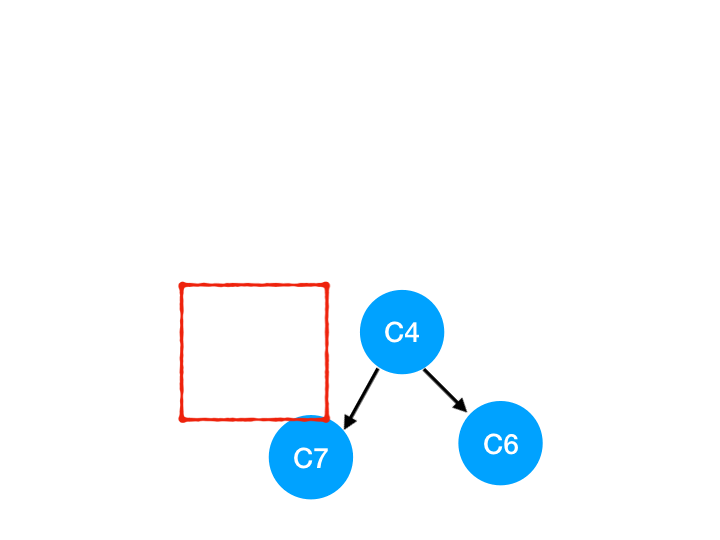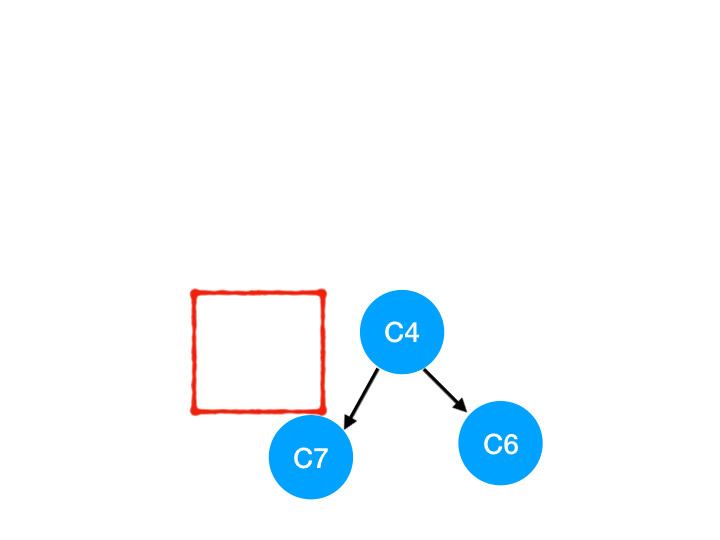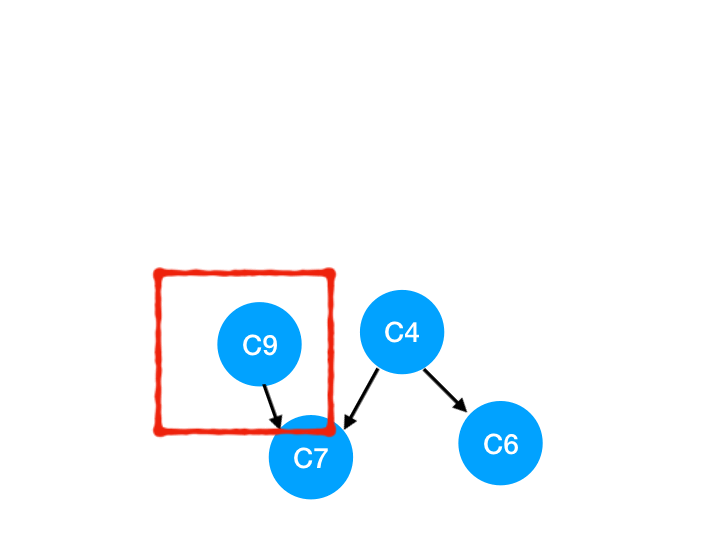
那么 C9 所指的 C7 的入度- 1.
| C6 | C7 | |
|---|---|---|
| 入度 | <span >1 | <span >1 |
這里 C7 的入度并不為 0,還不能加入 queue,
此時 queue = [C4]
接著執行 C4,
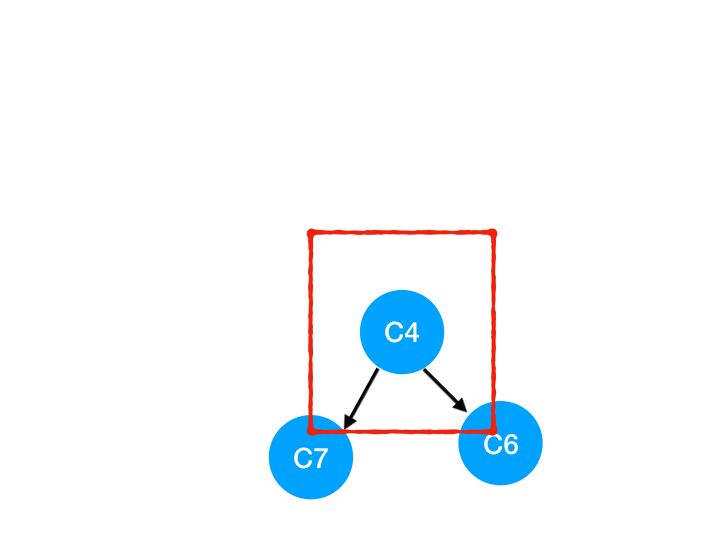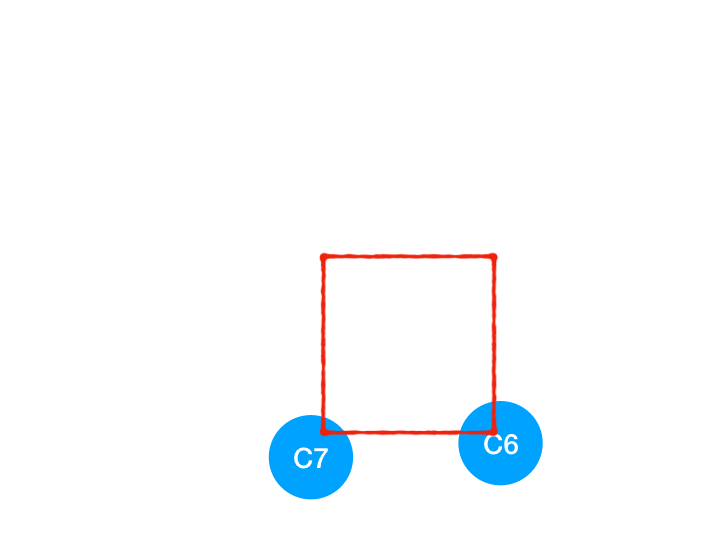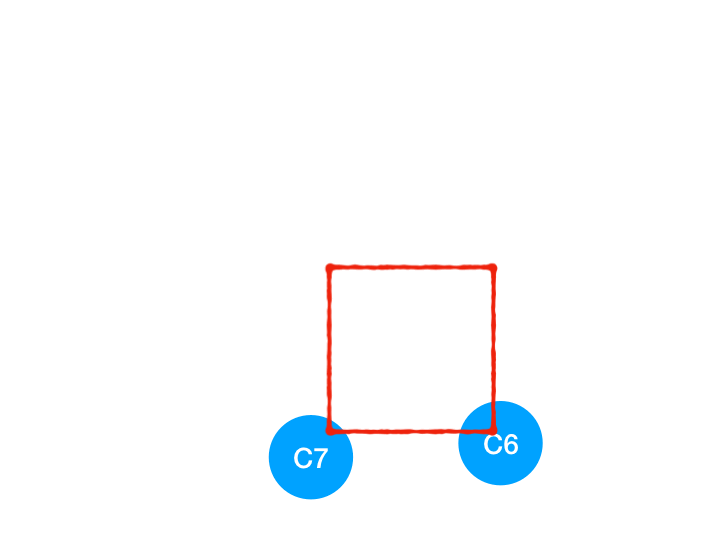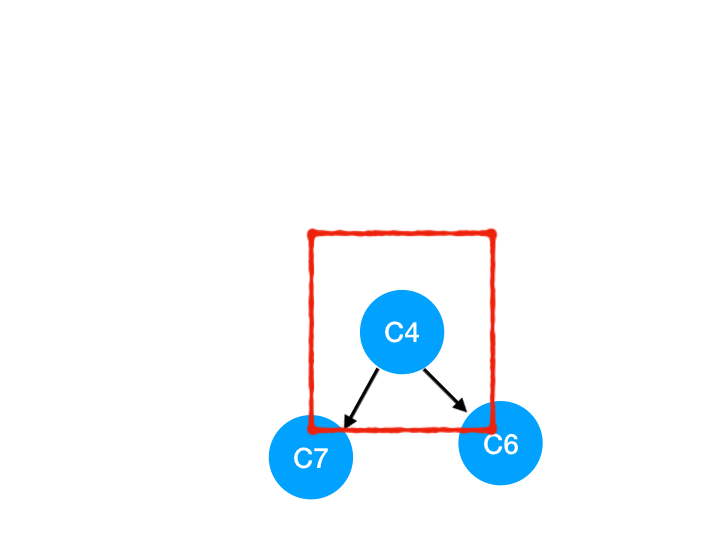
所以 C4 所指向的 C6 和 C7 的入度-1,
更新表格:
| C6 | C7 | |
|---|---|---|
| 入度 | <span >0 | <span >0 |
C6 和 C7 的入度都變成 0 啦!!把它們放入 queue,繼續執行到直到 queue 為空即可。
好了,那我們梳理一下這個算法:
<span >數據結構 這里我們的入度表格可以用 map 來存放,關于 map 還有不清楚的同學可以看之前我寫的 HashMap 的文章哦~
Map: <key = Vertex, value = 入度>
但實際代碼中,我們用一個 int array 來存儲也就夠了,graph node 可以用數組的 index 來表示,value 就用數組里的數值來表示,這樣比 Map 更精巧。
然后用了一個普通的 queue,用來存放可以被執行的那些 node.
<span >過程 我們把入度為 0 的那些頂點放入 queue 中,然后通過每次執行 queue 中的頂點,就可以讓依賴這個被執行的頂點的那些點的 入度-1,如果有頂點的入度變成了 0,就可以放入 queue 了,直到 queue 為空。
<span >細節 這里有幾點實現上的細節:
當我們 check 是否有新的頂點的 入度 == 0 時,沒必要過一遍整個 map 或者數組,只需要 check 剛剛改動過的就好了。
另一個是如果題目沒有給這個圖是 DAG 的條件的話,那么有可能是不存在可行解的,那怎么判斷呢?很簡單的一個方法就是比較一下最后結果中的頂點的個數和圖中所有頂點的個數是否相等,或者加個計數器,如果不相等,說明就不存在有效解。所以這個算法也可以用來判斷一個圖是不是有向無環圖。
很多題目給的條件可能是給這個圖的 edge list,也是表示圖的一種常用的方式。那么給的這個 list 就是表示圖中的邊。這里要注意審題哦,看清楚是誰 depends on 誰。其實圖的題一般都不會直接給你這個圖,而是給一個場景,需要你把它變回一個圖。
<span >時間復雜度
注意 ??:對于圖的時間復雜度分析一定是兩個參數,面試的時候很多同學張口就是 O(n)...
對于有 v 個頂點和 e 條邊的圖來說,
第一步,預處理得到 map 或者 array,需要過一遍所有的邊才行,所以是 O(e);
第二步,把 入度 == 0 的點入隊出隊的操作是 O(v),如果是一個 DAG,那所有的點都需要入隊出隊一次;
第三步,每次執行一個頂點的時候,要把它指向的那條邊消除了,這個總共執行 e 次;
總:O(v + e)
<span >空間復雜度
用了一個數組來存所有點的 indegree,之后的 queue 也是最多把所有的點放進去,所以是 O(v).
<span >代碼
關于這課程排序的問題,Leetcode 上有兩道題,一道是 207,問你能否完成所有課程,也就是問拓撲排序是否存在;另一道是 210 題,是讓你返回任意一個拓撲順序,如果不能完成,那就返回一個空 array。
這里我們以 210 這道題來寫,更完整也更常考一些。
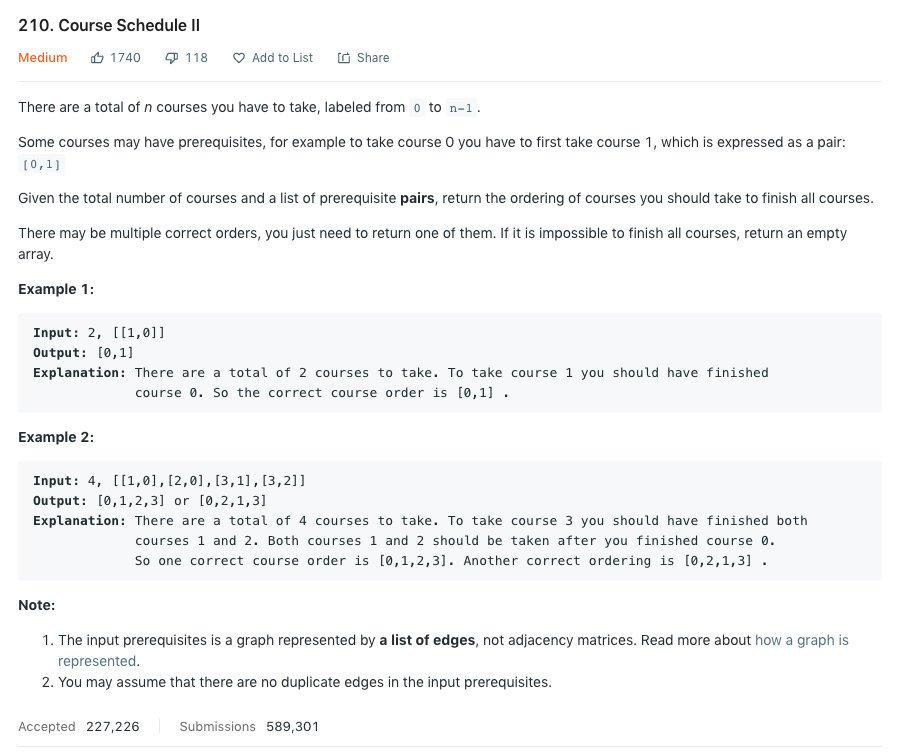
這里給的 input 就是我們剛剛說到的 edge list.
Example 1.
Input: 2, [[1,0]]
Output: [0,1]
Explanation: 這里一共 2 門課,1 的先修課程是 0. 所以正確的選課順序是[0, 1].
Example 2.
Input: 4, [[1,0],[2,0],[3,1],[3,2]]
Output: [0,1,2,3] or [0,2,1,3]
Explanation:這里這個例子畫出來如下圖
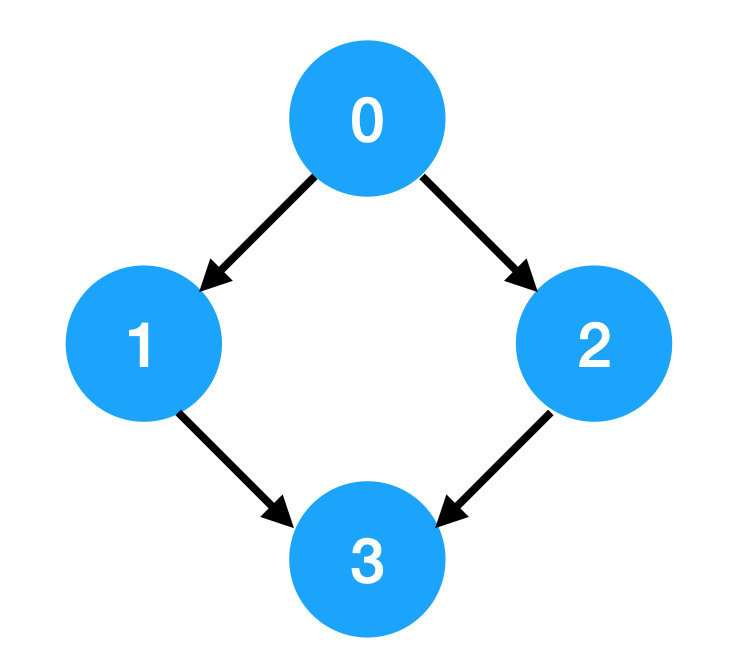
Example 3.
Input: 2, [[1,0],[0,1]]
Output: null
Explanation: 這課沒法上了
class Solution {
public int[] findOrder(int numCourses, int[][] prerequisites) {
int[] res = new int[numCourses];
int[] indegree = new int[numCourses];
// get the indegree for each course
for(int[] pre : prerequisites) {
indegree[pre[0]] ++;
}
// put courses with indegree == 0 to queue
Queue<Integer> queue = new ArrayDeque<>();
for(int i = 0; i < numCourses; i++) {
if(indegree[i] == 0) {
queue.offer(i);
}
}
// execute the course
int i = 0;
while(!queue.isEmpty()) {
Integer curr = queue.poll();
res[i++] = curr;
// remove the pre = curr
for(int[] pre : prerequisites) {
if(pre[1] == curr) {
indegree[pre[0]] --;
if(indegree[pre[0]] == 0) {
queue.offer(pre[0]);
}
}
}
}
return i == numCourses ? res : new int[]{};
}
}另外,拓撲排序還可以用 DFS - 深度優先搜索 來實現,限于篇幅就不在這里展開了,大家可以參考GeeksforGeeks的這個資料。
我們上文已經提到了它的一個 use case,就是選課系統,這也是最常考的題目。
而拓撲排序最重要的應用就是關鍵路徑問題,這個問題對應的是 AOE (Activity on Edge) 網絡。
AOE 網絡:頂點表示事件,邊表示活動,邊上的權重來表示活動所需要的時間。
AOV 網絡:頂點表示活動,邊表示活動之間的依賴關系。
在 AOE 網中,從起點到終點具有最大長度的路徑稱為關鍵路徑,在關鍵路徑上的活動稱為關鍵活動。AOE 網絡一般用來分析一個大項目的工序,分析至少需要花多少時間完成,以及每個活動能有多少機動時間。
具體是怎么應用分析的,大家可以參考這個視頻 的 14 分 46 秒,這個例子還是講的很好的。
其實對于任何一個任務之間有依賴關系的圖,都是適用的。
比如 pom 依賴引入 jar 包時,大家有沒有想過它是怎么導進來一些你并沒有直接引入的 jar 包的?比如你并沒有引入 aop 的 jar 包,但它自動出現了,這就是因為你導入的一些包是依賴于 aop 這個 jar 包的,那么 maven 就自動幫你導入了。
其他的實際應用,比如說:
語音識別系統的預處理;
管理目標文件之間的依賴關系,就像我剛剛說的 jar 包導入;
深度學習中的網絡結構處理。
感謝各位的閱讀!關于“web開發中拓撲排序是什么”這篇文章就分享到這里了,希望以上內容可以對大家有一定的幫助,讓大家可以學到更多知識,如果覺得文章不錯,可以把它分享出去讓更多的人看到吧!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。