KM算法詳解及如何使用java實現

今天就跟大家聊聊有關KM算法詳解及如何使用java實現，可能很多人都不太了解，為了讓大家更加了解，小編給大家總結了以下內容，希望大家根據這篇文章可以有所收獲。

匈牙利算法

基本概念

• 二分圖:二分圖又稱為二部圖.簡單來說，如果圖中點可以被分為兩組，并且使得所有邊都跨越組的邊界，則這就是一個二分圖。準確地說：把一個圖的頂點劃分為兩個不相交集 U 和V ，使得每一條邊都分別連接U、V中的頂點。如果存在這樣的劃分，則此圖為一個二分圖。二分圖的一個等價定義是：不含有"含奇數條邊的環"的圖。生成子圖:子圖包含原圖的所有頂點

• 匹配: 通俗的說:匹配（matching）是一個邊的集合，其中任意兩條邊都沒有公共頂點.定義:對給定二分圖G,在G的子圖M中,M的邊集{E}中的任意兩條邊不依賴于同一個頂點,則稱M為一個匹配

• 最大匹配: 圖的所有匹配中,含有邊數最多的匹配稱為最大匹配

• 完備匹配: 如果圖G的某個匹配M,使G的每個頂點都和匹配M中的某條邊相關聯,則稱M為完全匹配(完備匹配); 完備匹配一定是最大匹配.

• ?

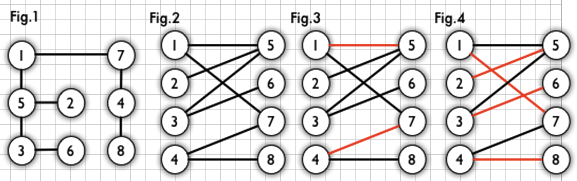
• 如圖: Fig.1為一個二分圖,將其改為Fig.2的形式更為直觀;Fig.3 紅線部分,為一個匹配; Fig.4 為一個最大匹配,也是一個完備匹配

求圖最大匹配的匈牙利算法

• 求最大匹配最直接暴力的方法是: 找出全部匹配,然后保留邊最多的. 這個方法的復雜度為邊數目的指數級函數. 匈牙利算法是效率更高的方法.

• 增廣路徑: 若P是圖G一條連通兩個未匹配點的路徑,并且屬于匹配M的邊和不屬于M的邊(即已匹配邊和未匹配邊)在P上交替出現,則稱P為相對于M的一條增廣路徑.

• ?

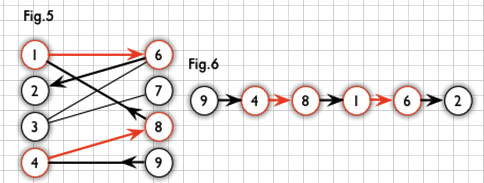
• 如上圖,Fig.5紅色為匹配,Fig.6為相對于匹配的一條增廣路徑

• 由增廣路徑的定義,可以推出三個結論:

1. P的路徑長度必定為奇數,第一條邊和最后一條邊都不屬于M;

2. P經過取反操作,可以得到一個更大的匹配M1;

3. M為G的最大匹配當且僅當不存在相對于M的增廣路徑.

• 匈牙利算法: 用增廣路徑求最大匹配(匈牙利科學家Edmonds于1965年提出); 其框架如下:

1. 置M為空;

2. 找出一條增廣路徑P,通過取反操作,得到更大的匹配M1;

3. 重復步驟2,直到找不出增廣路徑為止.

• 匈牙利算法實現(java)

• ?

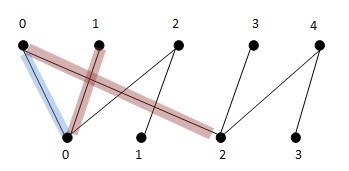
• 增廣路徑有兩種尋徑方法，一個是深搜(DFS)，一個是寬搜(BFS)。如上圖,藍色線為第一次匹配子圖,現在從x1尋找增廣路徑,如果是DFS深搜:首先:x1找到y0,發現y0已經被x0匹配,于是深入到x0,為x0找新的匹配點,發現x0可以匹配y2,讓x0與y2匹配,然后讓x1與y0匹配,得到第二次匹配子圖(紅色).現在,從x2出發,搜尋增廣路徑,x2找到y0匹配，但發現y0已經被x1匹配了，于是就深入到x1，去為x1找新的匹配節點，結果發現x1沒有其他的匹配節點，于是匹配失敗，x2接著找y1，發現y1可以匹配，于是就找到了新的增廣路徑,將x2-y1加入匹配中。

• DFS實現代碼見我的代碼java實現|GitHub

KM算法

KM算法原理

• 對于加權完全二分圖,找出權和最大的匹配,叫做求最佳匹配; 直接窮舉法:效率為n!;用KM算法.

• 定理: 設M是一個帶權完全二分圖G的一個完備匹配，給每個頂點一個可行頂標(第i個x頂點的可行標用lx[i]表示，第j個y頂點的可行標用ly[j]表示)，如果對所有的邊(i,j) in G,都有lx[i]+ly[j]>=w[i,j]成立(w[i,j]表示邊的權)，且對所有的邊(i,j) in M,都有lx[i]+ly[j]=w[i,j]成立，則M是圖G的一個最佳匹配。證明很容易。

• 對任意的G和M,可行標都是存在的

• 對二分圖G和一組可行標,滿足可行標邊界條件(lx[i]+ly[j]=w[i,j])的所有邊構成的生成子圖(需要包含所有頂點),稱為其等價子圖(相等子圖),在這個等價子圖上,尋找其完備匹配,如果完備匹配存在,則這個完備匹配M就是圖G的最大權匹配,最大權等于所有可行標的和; 如果完備匹配不存在,則修改可行標,用貪心的思想,將最優的邊加入等價子圖. KM算法就是一種逐次修改可行頂標的方法,使之對應的等價子圖逐次增廣(增加邊),最后出現完備匹配.

KM算法流程及實例

• Kuhn－Munkras算法流程：

1. 初始化可行頂標的值

2. 用匈牙利算法在等價子圖中尋找完備匹配

3. 若未找到完備匹配則修改可行頂標的值

4. 重復(2)(3)直到找到相等子圖的完備匹配為止

• 實例解釋算法過程:

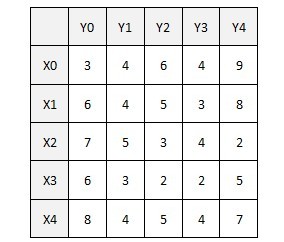
• 帶權二分圖如下:

• ?

• ?

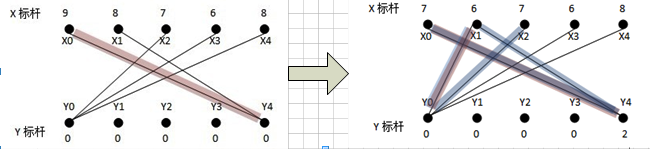
• 從x0找增廣路徑，找到x0-y4；然后,從x1找不到增廣路徑,這時,需要修改頂標,加入一條最優的新邊到等價子圖中:此時搜索過的路徑為x1-y4-x0(用匈牙利法DFS),在路徑上的X頂點集為S(x0,x1),Y頂點集為T(y4),對所有在S中的點xi及不在T中的點yj，計算d=min{(L(xi)+L(yj)-weight(xiyj))}，S中的點的頂標減去d,T中的點的頂標加上d,保持頂標依然為可行頂標.(這個d計算的意義是貪心思想,兩種情況:此時讓x0與其他點匹配,x1與y4匹配;x0依舊與y4匹配,x1找其他點匹配.d計算的是找到一條新加的邊,讓x0和x1都搭配后,與x0和x1都同y4搭配的非法搭配這種情況相比,損失的權重值最少).具體來說:此時算出來的最小d=L(X1)+L(Y0)-weight(X1Y0)=2,對頂標進行松弛后,得到的等價子圖如上,加了一條邊x1-y0,為x1重新找增廣路徑,找到x1-y0,此時匹配權值和為9+6=15;原來的非法匹配權值和為9+8=17,"損失"的權值最少為2(即加入一條其他的非x1-y0的邊如x0-y2,損失的權值為3,比2大,即貪心思想,"損失最小").

• KM算法原本的時間復雜度為O(n^{4),n個節點找n次增廣路徑,在某次找增光路徑之中,頂標最多改變n次,修改頂標的松弛量需n2;} 可改進為O(n^{3)時間復雜度:在尋找增廣路徑時順便將slack值算出.}

看完上述內容，你們對KM算法詳解及如何使用java實現有進一步的了解嗎？如果還想了解更多知識或者相關內容，請關注億速云行業資訊頻道，感謝大家的支持。