您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
這期內容當中小編將會給大家帶來有關python中如何理解算法的度量,文章內容豐富且以專業的角度為大家分析和敘述,閱讀完這篇文章希望大家可以有所收獲。
這里要評估一下這個算法到底效果如何。 評價的度量是有很多種的, 不同的場景使用的度量也不盡相同。 詳情如下。
首先這些都是監督學習, 也就是說都是有標記的數據。 而如何度量和評價機器學習算法呢, 還是要分成分類和回歸兩種問題分別來討論。
對于分類, 我們用Pima Indians onset of diabetes dataset。 算法呢用的是邏輯回歸。 注意邏輯回歸并不是回歸算法而是分類算法。 使用了一個sigmond的函數做了處理, 結果在0和1 之間。
對于回歸, 用的是波士頓房價的數據集。 算法呢, 就是以線性回歸為例。
對于分類問題, 有很多的度量都可以來評價這個算法的好壞, 但是側重點略有不同。 以下分別討論。
Classification Accuracy. 分類準確性
Logarithmic Loss. 對數損失函數
Area Under ROC Curve. ROC, AUC
Confusion Matrix.混淆矩陣
Classication Report. 分類報表
分類準確性是正確預測的數量占蘇哦有預測的比例。 最常規的參數, 也是最沒用的? 因為它只是適用于各種分類相同數量的情況, 而這并不常見。 評價的過于單一。 詳細的例子略。
比如下面說的:
accuracy是最常見也是最基本的evaluation metric。但在binary classification 且正反例不平衡的情況下,尤其是我們對minority class 更感興趣的時候,accuracy評價基本沒有參考價值。
什么fraud detection(欺詐檢測),癌癥檢測,都符合這種情況。舉個栗子:在測試集里,有100個sample,99個反例,只有1個正例。如果我的模型不分青紅皂白對任意一個sample都預測是反例,那么我的模型的accuracy是 正確的個數/總個數 = 99/100 = 99%你拿著這個accuracy高達99%的模型屁顛兒屁顛兒的去預測新sample了,而它一個正例都分不出來,有意思么。。。也有人管這叫accuracy paradox。
用的不多, 僅作了解。
對數損失函數也是一種評估預測準確性的方式, 變量的值在0-1之間。 看了一些例子, 經常用來判斷邏輯回歸的性能。 例子如下。
# Cross Validation Classification LogLoss
from pandas import read_csv
from sklearn.model_selection import KFold
from sklearn.model_selection import cross_val_score
from sklearn.linear_model import LogisticRegression
filename = 'pima-indians-diabetes.data.csv'
names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
dataframe = read_csv(filename, names=names)
array = dataframe.values
X = array[:,0:8]
Y = array[:,8]
kfold = KFold(n_splits=10, random_state=7)
model = LogisticRegression()
scoring = 'neg_log_loss'
results = cross_val_score(model, X, Y, cv=kfold, scoring=scoring)
print("Logloss: %.3f (%.3f)") % (results.mean(), results.std())
# Logloss: -0.493 (0.047)不理解為什么是負的, 所以簡單查了一些。 有人說負的是有問題的。 而值如果接近于是0 是更好的選擇。 https://stackoverflow.com/questions/21443865/scikit-learn-cross-validation-negative-values-with-mean-squared-error Yes, this is supposed to happen. The actual MSE is simply the positive version of the number you're getting.
https://stackoverflow.com/questions/21050110/sklearn-gridsearchcv-with-pipeline
Those scores are negative MSE scores, i.e. negate them and you get the MSE. The thing is that GridSearchCV, by convention, always tries to maximize its score so loss functions like MSE have to be negated.
MSE(均方差、方差):Mean squared error 這個再理解以下吧, 也許象有人說的, 其實是有些問題的。
ROC(receiver operating characteristic curve)是曲線, 比如以下。 
在ROC空間,ROC曲線越凸向左上方向效果越好。
AUC 是啥意思呢就是下面的面積。 那么聰明的你一定想得到,ROC曲線下方所包圍的面積越大,那么分類器的性能越優越。這個曲線下的面積,就叫做AUC(Area Under the Curve)。因為整個正方形的面積為1,所以0<=AUC<=1。
# Cross Validation Classification ROC AUC
from pandas import read_csv
from sklearn.model_selection import KFold
from sklearn.model_selection import cross_val_score
from sklearn.linear_model import LogisticRegression
filename = 'pima-indians-diabetes.data.csv'
names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
dataframe = read_csv(filename, names=names)
array = dataframe.values
X = array[:,0:8]
Y = array[:,8]
kfold = KFold(n_splits=10, random_state=7)
model = LogisticRegression()
scoring = 'roc_auc'
results = cross_val_score(model, X, Y, cv=kfold, scoring=scoring)
print("AUC: %.3f (%.3f)") % (results.mean(), results.std())
# AUC: 0.824 (0.041)混淆矩陣可以度量二分類,以及多分類問題。 這個對多分類的處理是它的優點。 考慮到自己方向和時間的問題, 沒有做進一步的探討, 只是把代碼運行了以下。
# Cross Validation Classification Confusion Matrix from pandas import read_csv from sklearn.model_selection import train_test_split from sklearn.linear_model import LogisticRegression from sklearn.metrics import confusion_matrix filename = 'pima-indians-diabetes.data.csv' names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class'] dataframe = read_csv(filename, names=names) array = dataframe.values X = array[:,0:8] Y = array[:,8] test_size = 0.33 seed = 7 X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=test_size, random_state=seed) model = LogisticRegression() model.fit(X_train, Y_train) predicted = model.predict(X_test) matrix = confusion_matrix(Y_test, predicted) print(matrix)
[[141 21] [ 41 51]]
這個其實才是最常用的。 應該理解清楚才行。
precision, recall, F1-score and support for each class
精確率
召回率
F1
下面是之前摘抄的一段, 應該是知乎的解釋, 應該比較清楚
關于準確率 來個例子 現在我先假定一個具體場景作為例子。 假如某個班級有男生80人,女生20人,共計100人.目標是找出所有女生. 現在某人挑選出50個人,其中20人是女生,另外還錯誤的把30個男生也當作女生挑選出來了. 作為評估者的你需要來評估(evaluation)下他的工作
首先我們可以計算準確率(accuracy),其定義是: 對于給定的測試數據集,分類器正確分類的樣本數與總樣本數之比。也就是損失函數是0-1損失時測試數據集上的準確率[1].
很容易,我們可以得到:他把其中70(20女+50男)人判定正確了,而總人數是100人,所以它的accuracy就是70 %(70 / 100). 這個值在一些時候是有意義的,但是很多情況準確率高并不意味著這個算法就好。 比如說1千萬頁面, google 選擇孫楊相關得, 實際一共是100頁面。 在這種情況下, 算法是永遠返回錯誤, 那么正確率是 100/10000000 高達99.999% 但是實際上是沒有意義得。 比如引入新得判斷標準。
header 1 |相關, 正類 | Nonrelevant 負類 ---|--- | --- 被檢索到 判斷成正確得 | TUre positives TP 正類判斷為正類, 例子中就是說正確得認為女生是女生 | False positive FP 就是說負類判斷錯誤了,成了正類。例子中男生被判斷成了女生。 未被檢索到 判斷成錯誤得 | falsenegatives FN 正類被判斷成了負類。 女生被判斷錯誤成了男生。 | true negatives TN 男生是男生, 正確判斷, 負類是負類。
TP FP 都是判斷成了正確得, 其實TP 是對得, FP 是錯誤判斷。
FN TN 都判斷成了負類, FN 判斷錯了, TN 是判斷對了。
TP FN 都是正類, TP 判斷成了正類, FN 判斷成了負類, 是錯得。
FP TN 都是男生, FP 判斷錯了成了女生。 TN 就是判斷正確是男生。 首先 TP-20, FP-30 FN 0 TN 50 精確率T 就是 TP/(TP+FP)= 20/(20+30) 所有正確被檢索得占實際被檢索到得比例。 召回率R, TP/(TP+FN)所有被檢索得占應該檢索得。 20/(20+0) 100% 不是說要召回, 而是說應該檢索得里面多少正確得檢索了。 F1值是精確率和召回率得調和均值。
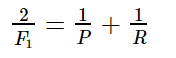

F1-measure 認為精確率和召回率的權重是一樣的
# Cross Validation Classification Report from pandas import read_csv from sklearn.model_selection import train_test_split from sklearn.linear_model import LogisticRegression from sklearn.metrics import classification_report filename = 'pima-indians-diabetes.data.csv' names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class'] dataframe = read_csv(filename, names=names) array = dataframe.values X = array[:,0:8] Y = array[:,8] test_size = 0.33 seed = 7 X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=test_size, random_state=seed) model = LogisticRegression() model.fit(X_train, Y_train) predicted = model.predict(X_test) report = classification_report(Y_test, predicted) print(report)
precision recall f1-score support 0.0 0.77 0.87 0.82 162 1.0 0.71 0.55 0.62 92 avg / total 0.75 0.76 0.75 254
這里關于回歸算法的度量, 三種:
Mean Absolute Error MAE 平均絕對誤差是絕對誤差的平均值
Mean Squared Error MSE 均方誤差是指參數估計值與參數真值之差平方的期望值;
R2
這個用的是絕對值 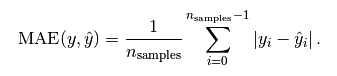
# Cross Validation Regression MAE
from pandas import read_csv
from sklearn.model_selection import KFold
from sklearn.model_selection import cross_val_score
from sklearn.linear_model import LinearRegression
filename = 'housing.csv'
names = ['CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', 'DIS', 'RAD', 'TAX', 'PTRATIO',
'B', 'LSTAT', 'MEDV']
dataframe = read_csv(filename, delim_whitespace=False, names=names)
array = dataframe.values
X = array[:,0:13]
Y = array[:,13]
kfold = KFold(n_splits=10, random_state=7)
model = LinearRegression()
scoring = 'neg_mean_absolute_error'
results = cross_val_score(model, X, Y, cv=kfold, scoring=scoring)
print("MAE: %.3f (%.3f)") % (results.mean(), results.std())
# MAE: -4.005 (2.084)插播 -- 其實在調試過程 遇到了個問題 “invalid literal for float():xx” 愿意你是什么呢, 是因為在導入數據的時候沒有設置正確的分割符。
dataframe = read_csv(filename, delim_whitespace=True, names=names)
--》
dataframe = read_csv(filename, delim_whitespace=False, names=names)
如果遇到這種問題不知道如何解決怎么辦, 把數據打印出來看看就會有思路的。
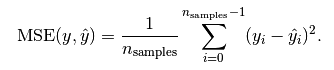
這個應用應該是最廣的,因為他能夠求導,所以經常作為loss function。計算的結果就是你的預測值和真實值的差距的平方和。
# Cross Validation Regression MSE
from pandas import read_csv
from sklearn.model_selection import KFold
from sklearn.model_selection import cross_val_score
from sklearn.linear_model import LinearRegression
filename = 'housing.csv'
names = ['CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', 'DIS', 'RAD', 'TAX', 'PTRATIO',
'B', 'LSTAT', 'MEDV']
dataframe = read_csv(filename, delim_whitespace=False, names=names)
array = dataframe.values
X = array[:,0:13]
Y = array[:,13]
num_folds = 10
kfold = KFold(n_splits=10, random_state=7)
model = LinearRegression()
scoring = 'neg_mean_squared_error'
results = cross_val_score(model, X, Y, cv=kfold, scoring=scoring)
print("MSE: %.3f (%.3f)") % (results.mean(), results.std())
# MSE: -34.705 (45.574)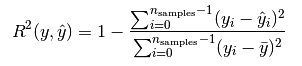
就是說每個值和與預測值的差的平方和除以每個值和平均值的差的平方和。 最后用1減以下, 如果大小接近1 就是很好的。
# Cross Validation Regression R^2
from pandas import read_csv
from sklearn.model_selection import KFold
from sklearn.model_selection import cross_val_score
from sklearn.linear_model import LinearRegression
filename = 'housing.csv'
names = ['CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', 'DIS', 'RAD', 'TAX', 'PTRATIO',
'B', 'LSTAT', 'MEDV']
dataframe = read_csv(filename, delim_whitespace=False, names=names)
array = dataframe.values
X = array[:,0:13]
Y = array[:,13]
kfold = KFold(n_splits=10, random_state=7)
model = LinearRegression()
scoring = 'r2'
results = cross_val_score(model, X, Y, cv=kfold, scoring=scoring)
print("R^2: %.3f (%.3f)") % (results.mean(), results.std())
# R^2: 0.203 (0.595)比較 首先從公式也能看出來,這三個基本上是R^2算一類,然后MSE和MAE算另一類。為什么呢?因為R^2相當于是對所有的數據都會有一個相同的比較標準。也就是說你得到一個值0.9999,那就非常好(當然對不同的應用你對好的定義可能會不一樣,比如某些你覺得0.6就夠了,某些你要0.8)。而MAE和MSE就是數據相關了,范圍可以非常大,你單純根據一個值完全不知道效果怎么樣。就是說R2 的值是0-1, 然后呢另外兩個是不同的, 范圍可能很大。
上述就是小編為大家分享的python中如何理解算法的度量了,如果剛好有類似的疑惑,不妨參照上述分析進行理解。如果想知道更多相關知識,歡迎關注億速云行業資訊頻道。
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。