如何實現尋找兩個正序數組的中位數

本篇內容介紹了“如何實現尋找兩個正序數組的中位數”的有關知識，在實際案例的操作過程中，不少人都會遇到這樣的困境，接下來就讓小編帶領大家學習一下如何處理這些情況吧！希望大家仔細閱讀，能夠學有所成！

題目

尋找兩個正序數組的中位數

描述

難度：困難

給定兩個大小分別為 m 和 n 的正序（從小到大）數組 nums1 和 nums2。請你找出并返回這兩個正序數組的 中位數 。

示例 1：

輸入：nums1 = [1,3], nums2 = [2]
輸出：2.00000
解釋：合并數組 = [1,2,3] ，中位數 2

示例 2：

輸入：nums1 = [1,2], nums2 = [3,4]
輸出：2.50000
解釋：合并數組 = [1,2,3,4] ，中位數 (2 + 3) / 2 = 2.5

示例 3：

輸入：nums1 = [0,0], nums2 = [0,0]
輸出：0.00000

示例 4：

輸入：nums1 = [], nums2 = [1]
輸出：1.00000

示例 5：

輸入：nums1 = [2], nums2 = []
輸出：2.00000

提示：

nums1.length == m
nums2.length == n
0 <= m <= 1000
0 <= n <= 1000
1 <= m + n <= 2000
-106 <= nums1[i], nums2[i] <= 106

Solution

解法

解題思路

從題目中透露的細節要求

• 中位數

• 兩個集合

• 兩個集合均為正序集合

• 找出這兩個正序集合的中位數

什么是中位數

• 首先需要正確理解中位數的概念，中位數是指，一個集合中，處于中間的數的數字，如果集合的長度為奇數，則為中間的數字，如果為偶數，則為中間兩個數的平均數

針對這道題，我們在計算中位數的時候需要區分最終的長度，最終是奇數還是偶數

合并兩個正序集合

找出兩個正序集合的中位數，首先第一反應想到的是合并兩個正序集合，合并兩個正序集合又帶來新的問題，保證排序后的新集合也是正序的，否則求出來的中位數的結果是不對的

合并兩個正序集合，簡單粗暴的做法是，直接使用JDK現成的API合并兩個數組，并且進行SORT排序，但是這樣會造成時間復雜度及空間復雜度增加，所以這里我們采用常見的雙指針的方式

雙指針

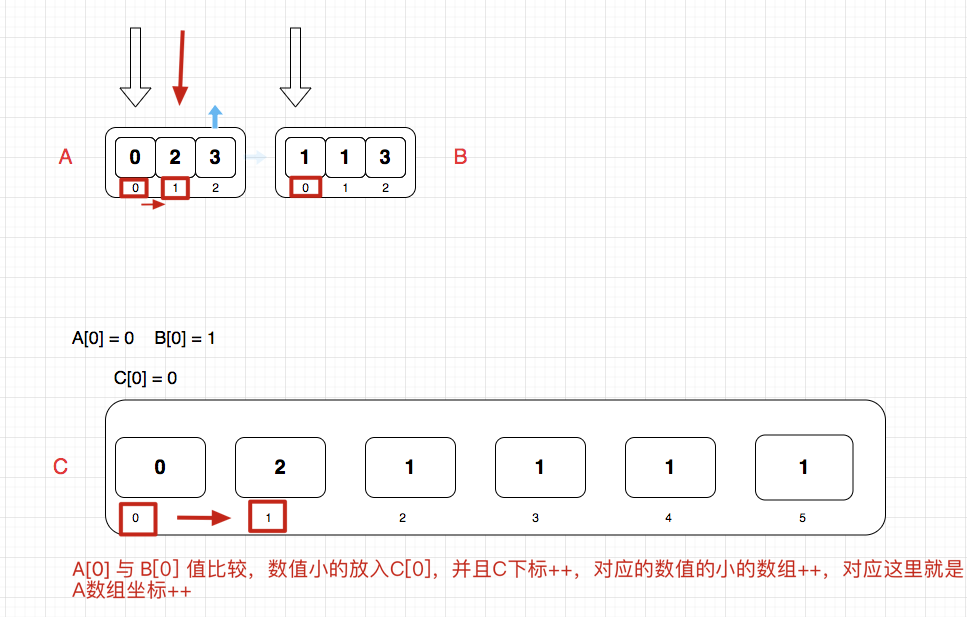
采用三個指針指向三個數組數組的當前下標，默認從0開始，判斷兩個老數組的初始坐標值，小的數據則放入到新的數組中，并且更新對應的下標，如下圖所示，A[0] < B[0] ，將A[0]的值賦值給C，C[0]=0 ,并且將C的坐標自增，同時A的值比較小，所以A的下標自增，B坐標不動，如此循環

當A的坐標，或B的坐標等于對應的數組集合長度時，說明對應的數組集合已經遍歷完了，我們則可以直接拼接對應另外一個集合到新的集合中即可，直到最終兩個集合拼接完成

拼接新的集合完成之后，判斷最終集合的長度為奇數還是偶數，最終取出中位數，返回即可

但其實我們也可以不需要完全合并兩個有序數組，只要找到中位數的位置即可，由于兩個數組的長度已知，因此中位數對應的兩個數組的下標之和也是已知的。在每次賦值完C之后，判斷當前C下標的值是否為中位數位置，如果是可直接計算中位數的值返回即可，整理的時間復雜度也會縮短一半

這里強調一點，必須要賦值完C，因為如果先判斷中位數，則C還沒有賦值完，最終的結果肯定是不對的

CODE

class Solution {
    public double findMedianSortedArrays(int[] nums1, int[] nums2) {
        int length2= nums1.length ;
        int length3= nums2.length ;
        int lengthSum = length2+length3;
        //是否偶數
        boolean type ;
        int half =0;;
        //偶數
        if(lengthSum%2 == 0){
            // half , half+1       8/2-1=4-1=3   [0,1,2,3,4,5,6,7]
            half = lengthSum/2-1;
            type= true;
        }else{
            //奇數      7/2=3
            half = lengthSum/2;
            type= false;
        }
        // num1下標
        int a = 0 ;
        // num2下標
        int b = 0 ;
        // newnums下標
        int c = 0 ;
        int[] newnums = new int[lengthSum];
        while(true){

            //a已經遍歷完了
            if(a==length2){
                newnums[c] = nums2[b];
                b++;
                //半數
                if(c==half&&!type){
                    return newnums[c]/1.0;
                }
                if(c==(half+1)&&type){
                    return (newnums[c]+newnums[c-1])/2.0;
                }

                c++;
                continue ;
            }
            //b已經遍歷完了
            if(b==length3){
                newnums[c] = nums1[a];
                a++;
                //半數
                if(c==half&&!type){
                    return newnums[c]/1.0;
                }
                if(c==(half+1)&&type){
                    return (newnums[c]+newnums[c-1])/2.0;
                }
                c++;
                continue ;
            }
            if(nums1[a] >= nums2[b]){
                newnums[c] = nums2[b];
                b++;
            }else{
                newnums[c] = nums1[a];
                a++;
            }
            //半數
            if(c==half&&!type){
                return newnums[c]/1.0;
            }
            if(c==(half+1)&&type){
                return (newnums[c]+newnums[c-1])/2.0;
            }
            c++;
        }
    }
}

復雜度

• 時間復雜度：O(m+n)，最長可能需要完全遍歷兩個數組

• 空間復雜度：O(1)

結果

• 執行用時：3 ms, 在所有 Java 提交中擊敗了82.60%的用戶

  內存消耗：39.7 MB, 在所有 Java 提交中擊敗了63.95%的用戶

我曾在銀色平原漫步,也曾在青草之河垂釣，這片土地認識我，我們若不堅強，就將滅亡

“如何實現尋找兩個正序數組的中位數”的內容就介紹到這里了，感謝大家的閱讀。如果想了解更多行業相關的知識可以關注億速云網站，小編將為大家輸出更多高質量的實用文章！