您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
這篇文章主要介紹“P、NP、NPC問題是什么”,在日常操作中,相信很多人在P、NP、NPC問題是什么問題上存在疑惑,小編查閱了各式資料,整理出簡單好用的操作方法,希望對大家解答”P、NP、NPC問題是什么”的疑惑有所幫助!接下來,請跟著小編一起來學習吧!
在計算復雜度理論中,P(也稱為PTIME或DTIME)是基本的復雜度類型。 它是指能夠使用確定圖靈機在多項式時間內解決的所有決策問題。
這里我們給一下P的定義,如果一個公式語言L是一個P類型,那么當且僅當存在這樣的一個確定圖靈機M時成立:
對于所有的輸入,M都會在多項式時間內運行
對于L中所有的x, M的輸出都是1
對于不在L中的所有x,M輸出都是0
常見的P問題包括線性規劃的決策版本,計算最大公因數和找到最大匹配。 在2002年,證明了確定數字是否為質數的問題也是一個P問題。
在計算復雜度理論中,NP(nondeterministic polynomial time)不確定性多項式時間主要用來衡量分類決策問題的復雜度。 NP是一組決策問題,對于這些問題實例來說,如果答案為“是”,那么表示該實例使用確定圖靈機可在多項式時間內驗證成功。
NP實際上是由兩個階段組成的,第一階段包括對解決方案的猜測,該階段以非確定性方式生成,而第二階段包括確定性算法,驗證猜測是否可以解決問題。也就是說NP= nondeterministic + polynomial。
根據P和NP的定義,我們可以發現所有的P問題都是NP問題,因為P的定義是所有問題都可以在多項式時間內確定地解決,而NP的定義是問題可以在多項式時間內得到驗證的問題。
但是NP包含了更多的問題,其中NP中最難的問題被稱為NP-complete 問題。解決多項式時間中的此類問題的算法也能夠解決多項式時間中的任何其他NP問題。
在計算機科學中,很多搜索優化的問題都可以被看做是NP問題。旅行商問題就是一個典型的NP問題。
“給出一個城市列表以及每對城市之間的距離,要找到一條訪問每個城市一次最后返回原城市的最短路徑” 這是組合優化中的一個NP難題,在理論計算機科學和運籌學中很重要。
因為NP問題中包含了很多實際生活中非常重要的問題,所以人們為查找NP中的多項式時間算法付出了巨大的努力。但是,NP中仍然存在許多問題,這些問題好像無法在多項式時間內得到解決。關于這些問題在多項式時間內是否能夠被解決是計算機科學中最大的未解決問題之一。
在這種情況下,引入了一個重要的概念就是NP完全決策問題集(NP-complete),它是NP的子集,可以非正式地描述為NP中“最難”的問題。如果我們說一個問題被證明是NPC問題,那么意味著在這個問題上無法找到多項式時間算法。
但是,在實際應用中,通常不會花費大量的計算去尋找一個最優解,但是可以在多項式時間內找到一個次優解,這對于實際應用就已經足夠了。
在計算復雜度理論中,滿足以下情況的問題是NPC問題:
一個不確定的圖靈機可以在多項式時間內求解。
確定性的Turing機可以在較大的時間復雜度中進行求解(EXPTIME或者暴力搜索算法),并且可以在多項式時間內驗證其解。
它可以用來模擬任何其他具有相似可解性的問題(NP中的其他問題都可以在多項式時間內轉換或者規約為該問題)。
根據規則3,因為NPC問題是NP問題的更加復雜的形式,如果你可以找到一個解決某個 NP-complete 問題的多項式算法,那么所有的 NP 問題都將可以很容易地解決。
舉個例子,一個一元一次方程可以規約為求一個一元二次方程,只需要將二次型系數變為0即可。通過不斷地規約,我們能得到復雜度更高但是應用范圍更廣的算法來代替復雜度雖低但是應用范圍小的一類問題的算法。
盡管可以“快速”驗證NPC問題的解決方案,但是沒有已知的方法可以快速找到解決方案。即,隨著問題的大小增長,使用任何當前已知的算法解決問題所需的時間迅速增加。
仍未發現用于計算NP完全問題的解決方案的方法,但是計算機科學家和程序員仍然經常遇到NP完全問題。 NP完全問題通常通過使用啟發式方法和近似算法來解決。
在計算復雜性理論中,NP-hard是對一類問題的描述,這些問題“至少與NP中最難的問題一樣難”。 NP-hard問題的一個簡單例子是子集和問題。
如果一個已知的NPC問題能夠規約到此問題,那么這個問題就叫做NP-hard問題。
所以NPC問題一定是NP-Hard問題,但并不是所有的NP-Hard問題都是NPC問題。
P和NP問題是計算機科學中尚未解決的主要問題。它談論的是如果一個問題可以快速的被驗證,那么該問題是否可以被快速解決?
P是指該問題能夠在多項式時間內找到解決方案,而NP是指如果找到候選的答案,則能夠進行快速驗證。
一般情況下大家都任務P != NP,也就是說雖然無法在多項式時間內解決,但答案可以在多項式時間內驗證。
根據P和NP是否相同,我們分別作出P、NP、NPC和NP-Hard的關系圖。
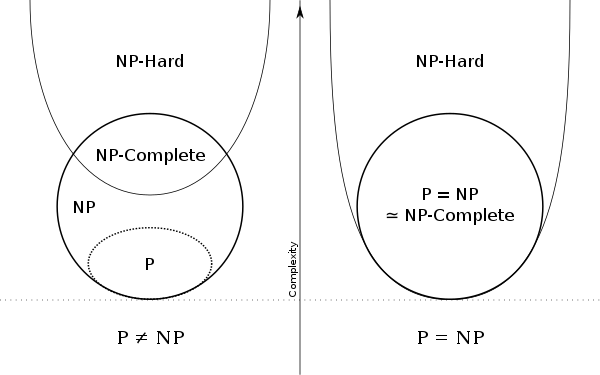
到此,關于“P、NP、NPC問題是什么”的學習就結束了,希望能夠解決大家的疑惑。理論與實踐的搭配能更好的幫助大家學習,快去試試吧!若想繼續學習更多相關知識,請繼續關注億速云網站,小編會繼續努力為大家帶來更多實用的文章!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。