您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
如何進行Redis GeoHash核心原理解析,相信很多沒有經驗的人對此束手無策,為此本文總結了問題出現的原因和解決方法,通過這篇文章希望你能解決這個問題。
小麥同學是個吃貨+技術宅,平日里就喜歡拿著手機地圖點點按按來查詢一些好玩的東西。某一天到北海公園游玩,肚肚餓了,于是乎打開手機地圖,搜索北海公園附近的餐館,并選了其中一家用餐。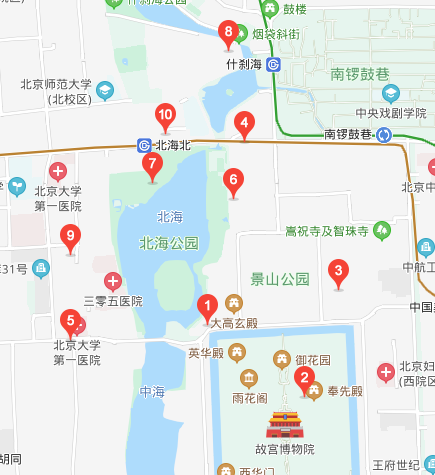
飽暖思yin欲的麥叔飯后思考地圖后臺如何根據自己所在位置查詢來查詢附近餐館的呢?苦思冥想了半天,小麥想出了個方法:計算所在位置P與北京所有餐館的距離,然后返回距離<=1000米的餐館。小得意了一會兒,小麥發現北京的餐館何其多啊,這樣計算不得了,于是想了,既然知道經緯度了,那它應該知道自己在西城區,那應該計算所在位置P與西城區所有餐館的距離啊,機機運用了遞歸的思想,想到了西城區也很多餐館啊,應該計算所在位置P與所在街道所有餐館的距離,這樣計算量又小了,效率也提升了。
小麥的計算思想很樸素,就是通過過濾的方法來減小參與計算的餐館數目,從某種角度上講,機機在使用索引技術。
一提到索引,大家腦子里馬上浮現出B樹索引,因為大量的數據庫(如MySQL、oracle、PostgreSQL等)都在使用B樹。B樹索引本質上是對索引字段進行排序,然后通過類似二分查找的方法進行快速查找,即它要求索引的字段是可排序的,一般而言,可排序的是一維字段,比如時間、年齡、薪水等等。但是對于空間上的一個點(二維,包括經度和緯度),如何排序呢?又如何索引呢?解決的方法很多,下文介紹一種方法來解決這一問題。
思想:如果能通過某種方法將二維的點數據轉換成一維的數據,那樣不就可以繼續使用B樹索引了嘛。那這種方法真的存在嘛,答案是肯定的。目前很火的GeoHash算法就是運用了上述思想,下面我們就開始GeoHash之旅吧。
先來兩個干貨,在線查看GPS某個區域的GeoHash值。
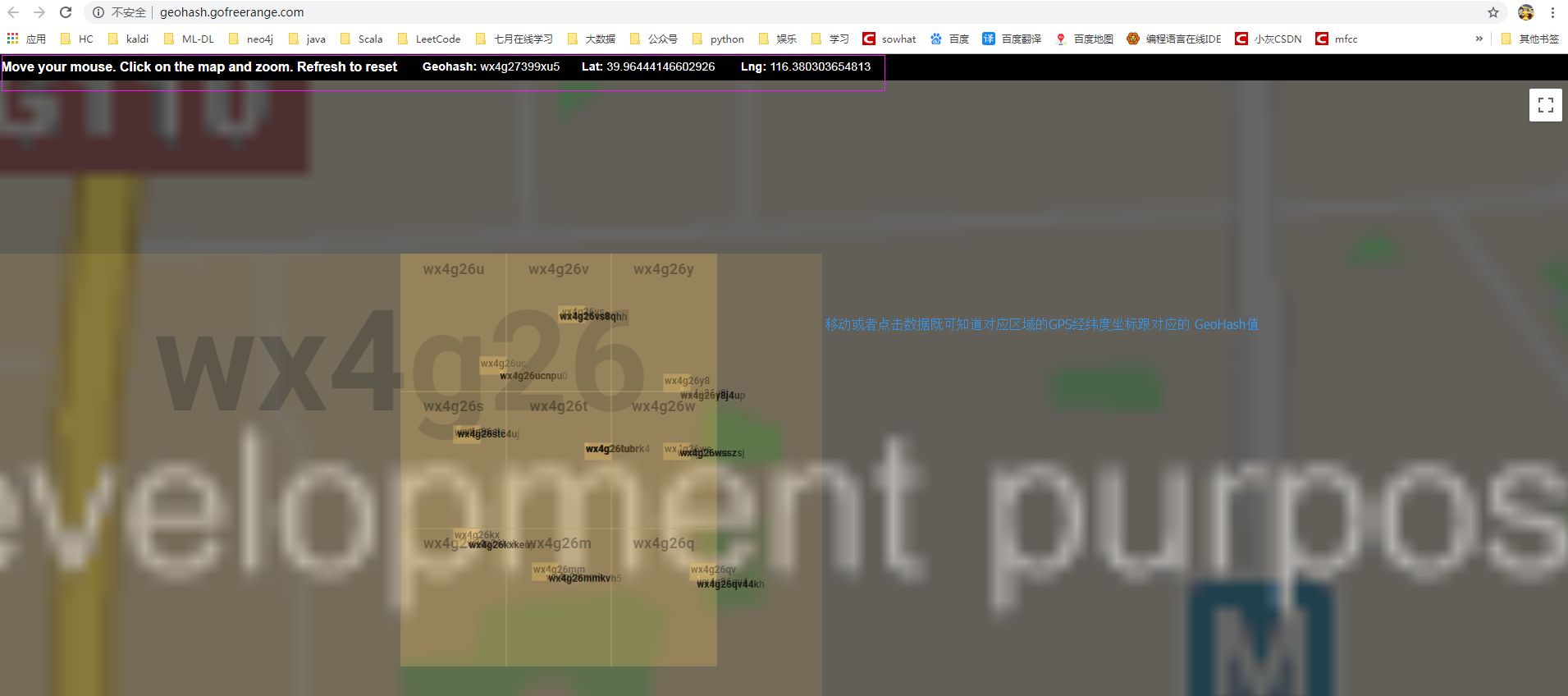
跟更好用些
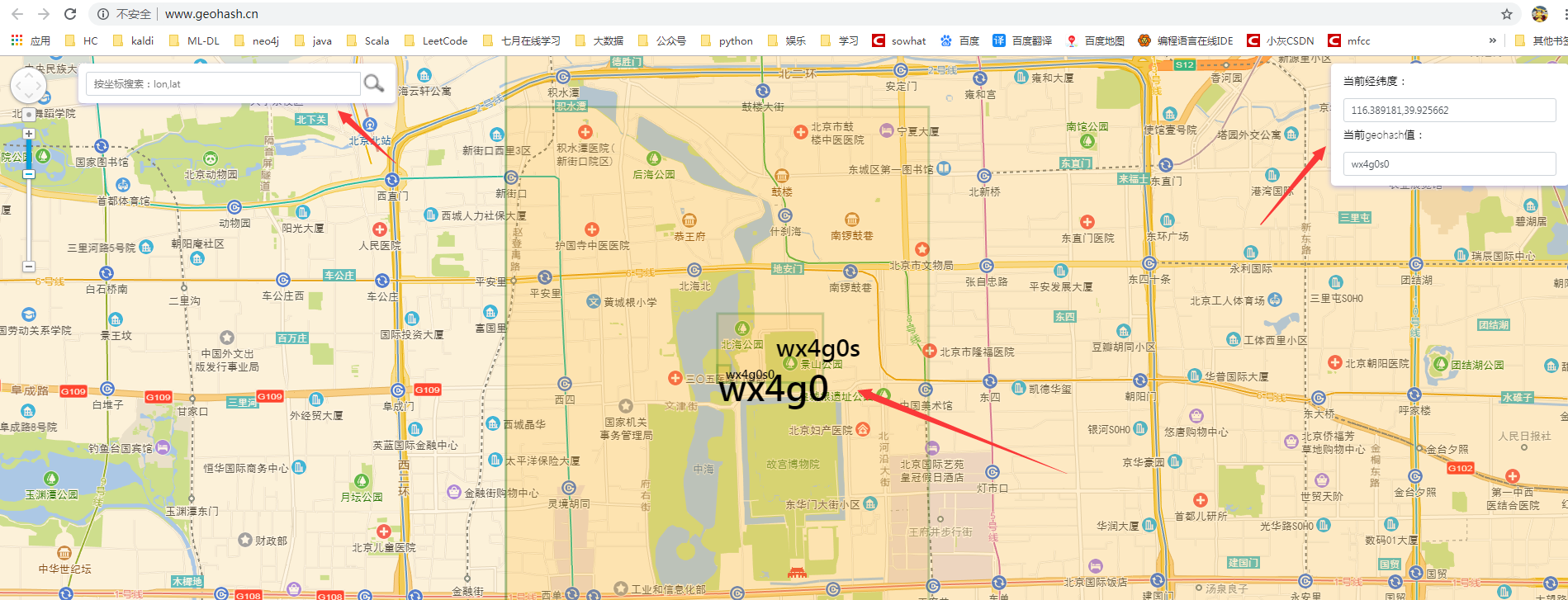
GeoHash將二維的經緯度轉換成字符串,比如下圖展示了北京9個區域的GeoHash字符串,分別是WX4ER,WX4G2、WX4G3等等,每一個字符串代表了某一矩形區域。也就是說,這個矩形區域內所有的點(經緯度坐標)都共享相同的GeoHash字符串,這樣既可以保護隱私(只表示大概區域位置而不是具體的點),又比較容易做緩存,比如左上角這個區域內的用戶不斷發送位置信息請求餐館數據,由于這些用戶的GeoHash字符串都是WX4ER,所以可以把WX4ER當作key,把該區域的餐館信息當作value來進行緩存,而如果不使用GeoHash的話,由于區域內的用戶傳來的經緯度是各不相同的,很難做緩存。
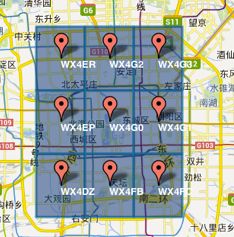
字符串越長,表示的范圍越精確。如圖所示,5位的編碼能表示10平方千米范圍的矩形區域,而6位編碼能表示更精細的區域(約0.34平方千米)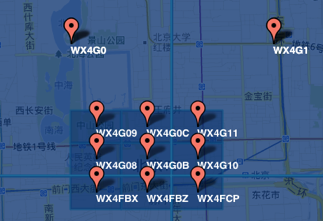
字符串相似的表示距離相近(特殊情況后文闡述),這樣可以利用字符串的前綴匹配來查詢附近的POI信息。如下兩個圖所示,第一個在城區,第二個在郊區,城區的GeoHash字符串之間比較相似,郊區的字符串之間也比較相似,而城區和郊區的GeoHash字符串相似程度要低些。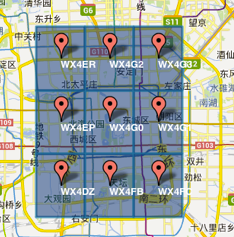
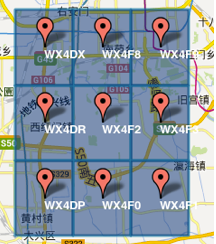
通過上面的介紹我們知道了GeoHash就是一種將經緯度轉換成字符串的方法,并且使得在大部分情況下,字符串前綴匹配越多的距離越近,回到我們的案例,根據所在位置查詢來查詢附近餐館時,只需要將所在位置經緯度轉換成GeoHash字符串,并與各個餐館的GeoHash字符串進行前綴匹配,匹配越多的距離越近。
下面以北海公園附近隨便一個位置為例介紹GeoHash算法的計算步驟,先用百度 GPS反定位系統查找看下經緯度。
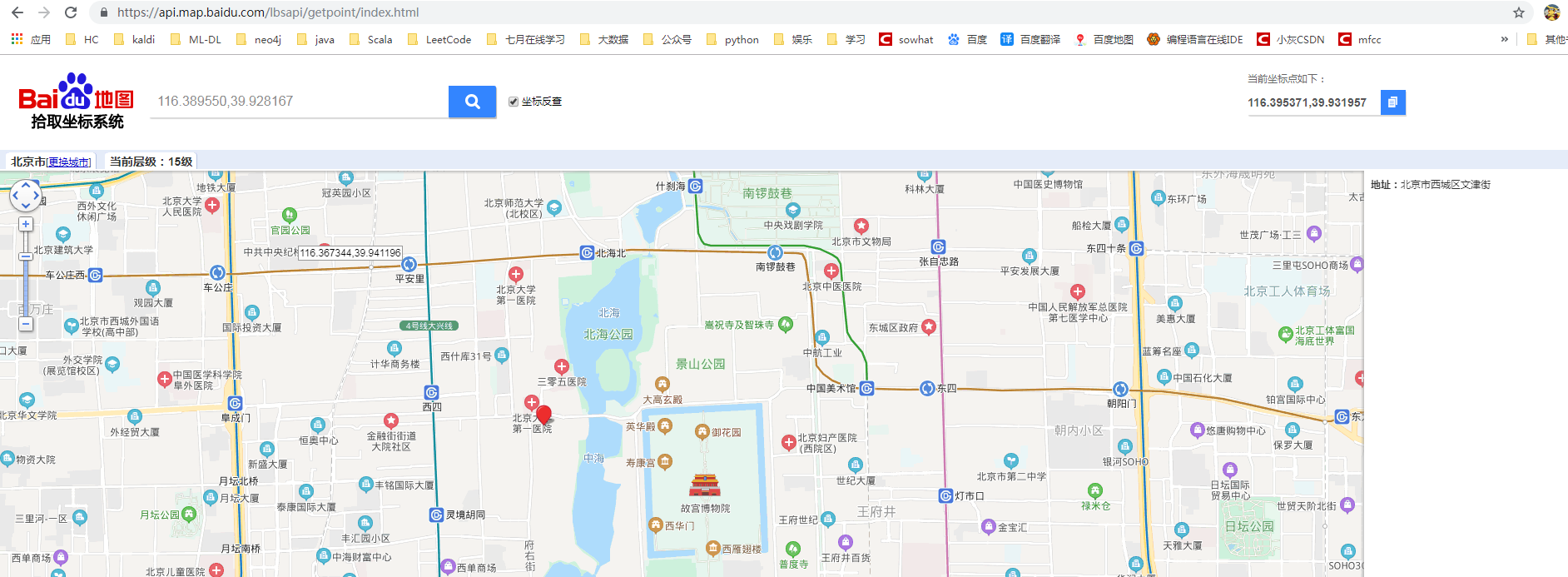
緯度=116.395371,經度=39.931957。
地球緯度區間是[-90,90], 北海公園的緯度是39.928167,可以通過下面算法對緯度39.928167進行逼近編碼:
區間[-90,90]進行二分為[-90,0),[0,90],稱為左右區間,可以確定39.928167屬于右區間[0,90],給標記為1;
接著將區間[0,90]進行二分為 [0,45),[45,90],可以確定39.928167屬于左區間 [0,45),給標記為0;
遞歸上述過程39.928167總是屬于某個區間[a,b]。隨著每次迭代區間[a,b]總在縮小,并越來越逼近39.928167;
如果給定的緯度x(39.928167)屬于左區間,則記錄0,如果屬于右區間則記錄1,這樣隨著算法的進行會產生一個序列1011100,序列的長度跟給定的區間劃分次數有關。
39.928167 根據緯度算編碼
| bit | min | mid | max |
|---|---|---|---|
| 1 | -90.000 | 0.000 | 90.000 |
| 0 | 0.000 | 45.000 | 90.000 |
| 1 | 0.000 | 22.500 | 45.000 |
| 1 | 22.500 | 33.750 | 45.000 |
| 1 | 33.750 | 39.375 | 45.000 |
| 0 | 39.375 | 42.188 | 45.000 |
| 0 | 39.375 | 40.7815 | 42.188 |
| 0 | 39.375 | 40.07825 | 40.7815 |
| 1 | 39.375 | 39.726625 | 40.07825 |
| 1 | 39.726625 | 39.9024375 | 40.07825 |
同理,地球經度區間是[-180,180],可以對經度116.389550進行編碼。根據經度算編碼
| bit | min | mid | max |
|---|---|---|---|
| 1 | -180 | 0.000 | 180 |
| 1 | 0.000 | 90 | 180 |
| 0 | 90 | 135 | 180 |
| 1 | 90 | 112.5 | 135 |
| 0 | 112.5 | 123.75 | 135 |
| 0 | 112.5 | 118.125 | 123.75 |
| 1 | 112.5 | 115.3125 | 118.125 |
| 0 | 115.3125 | 116.71875 | 118.125 |
| 1 | 115.3125 | 116.015625 | 116.71875 |
| 1 | 116.015625 | 116.3671875 | 116.71875 |
通過上述計算,緯度產生的編碼為10111 00011,經度產生的編碼為11010 01011。偶數位放經度,奇數位放緯度,把2串編碼組合生成新串:11100 11101 00100 01111。
最后使用用0-9、b-z(去掉a, i, l, o)這32個字母進行base32編碼,首先將11100 11101 00100 01111轉成十進制,對應著28、29、4、15,十進制對應的編碼就是wx4g。同理,將編碼轉換成經緯度的解碼算法與之相反,具體不再贅述。
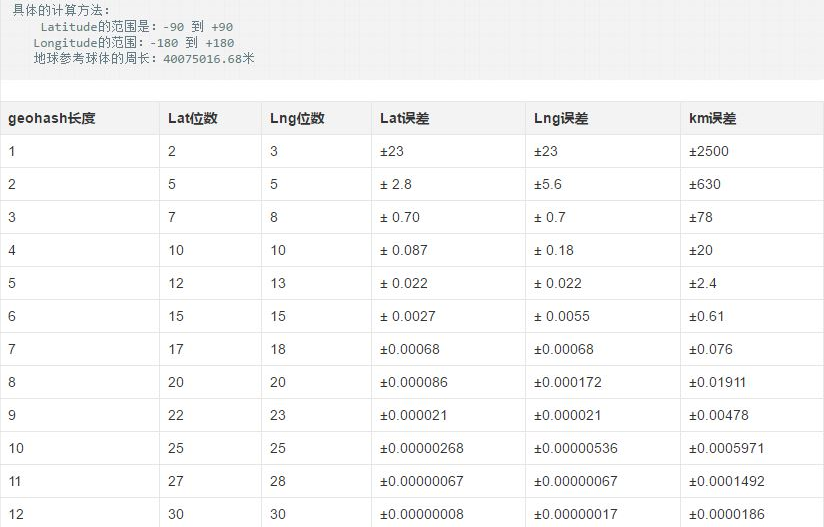
可以看出,當geohash base32編碼長度為8時,精度在19米左右,而當編碼長度為9時,精度在2米左右,編碼長度需要根據數據情況進行選擇。
經度每隔0.00001度,距離相差約1米;
每隔0.0001度,距離相差約10米;
每隔0.001度,距離相差約100米;
每隔0.01度,距離相差約1000米;
每隔0.1度,距離相差約10000米。
緯度每隔0.00001度,距離相差約1.1米;
每隔0.0001度,距離相差約11米;
每隔0.001度,距離相差約111米;
每隔0.01度,距離相差約1113米;
每隔0.1度,距離相差約11132米。
上文講了GeoHash的計算步驟,僅僅說明是什么而沒有說明為什么?為什么分別給經度和維度編碼?為什么需要將經緯度兩串編碼交叉組合成一串編碼?本節試圖回答這一問題。
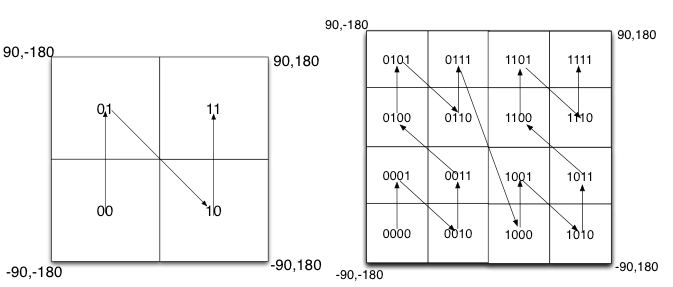
如下圖所示,我們將二進制編碼的結果填寫到空間中,當將空間劃分為四塊時候,編碼的順序分別是左下角00,左上角01,右下腳10,右上角11,也就是類似于Z的曲線,當我們遞歸的將各個塊分解成更小的子塊時,編碼的順序是自相似的(分形),每一個子快也形成Z曲線,這種類型的曲線被稱為Peano空間填充曲線。
這種類型的空間填充曲線的優點是將二維空間轉換成一維曲線(事實上是分形維),對大部分而言,編碼相似的距離也相近, 但Peano空間填充曲線最大的缺點就是突變性,有些編碼相鄰但距離卻相差很遠,比如0111與1000,編碼是相鄰的,但距離相差很大。
除Peano空間填充曲線外,還有很多空間填充曲線,如圖所示,其中效果公認較好是Hilbert空間填充曲線,相較于Peano曲線而言,Hilbert曲線沒有較大的突變。為什么GeoHash不選擇Hilbert空間填充曲線呢?可能是Peano曲線思路以及計算上比較簡單吧,事實上,Peano曲線就是一種四叉樹線性編碼方式。

由于GeoHash是將區域劃分為一個個規則矩形,并對每個矩形進行編碼,這樣在查詢附近POI信息時會導致以下問題,比如紅色的點是我們的位置,綠色的兩個點分別是附近的兩個餐館,但是在查詢的時候會發現距離較遠餐館的GeoHash編碼與我們一樣(因為在同一個GeoHash區域塊上),而較近餐館的GeoHash編碼與我們不一致。這個問題往往產生在邊界處。
解決的思路很簡單,我們查詢時,除了使用定位點的GeoHash編碼進行匹配外,還使用周圍8個區域的GeoHash編碼,這樣可以避免這個問題。
我們已經知道現有的GeoHash算法使用的是Peano空間填充曲線,這種曲線會產生突變,造成了編碼雖然相似但距離可能相差很大的問題,因此在查詢附近餐館時候,首先篩選GeoHash編碼相似的POI(point of interest)點,然后進行實際距離計算。
GeoHash只是空間索引的一種方式,特別適合點數據,而對線、面數據采用R樹索引更有優勢(可為什么需要空間索引)。
GeoHash值可以區分精度,位數越多,精度越高,表達的地理位置越精細;如一位的GeoHash值把地球劃分為32個矩形,8位的geohash值把地球劃分為32^8個小矩形
適合根據某個經緯度坐標position計算出GeoHash值,然后和數據庫中精度更高的GeoHash值做前綴比較
常見問題:如何根據自己所在位置查詢來查詢附近50米的POI(point of interest,比如商家、景點等)呢(圖1a)?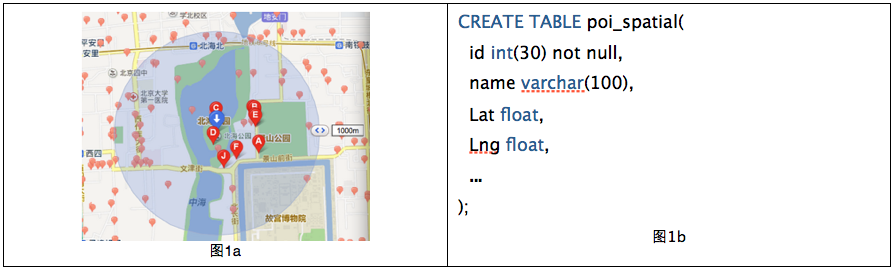
每個POI都有經緯度信息,用圖1b的SQL語句在mySQL中建立了POI_spatial的表,其中lat和lng兩個字段來代表緯度和經度。為后續分析方便起見,我人造了40萬個POI數據。
該方法的思路很直接:計算位置與所有POI的距離,并保留距離小于50米的POI。
插句題外話,計算經緯度之間的距離不能像求歐式距離那樣平方開根號,因為地球是個不規整的球體(圖2a),普通計算適合都是默認按最簡單的完美球體假設,兩點之間的距離函數應該如圖2b所示。

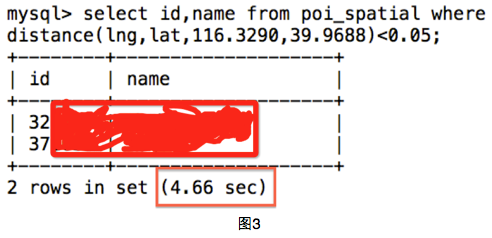
該方法的復雜度為:40萬*距離函數。我們將球體距離函數寫為mysql存儲過程distance,之后我們執行查詢操作(圖3),發現花費了4.66秒。
該方法采用逐步細化的方式,一般分為兩部:
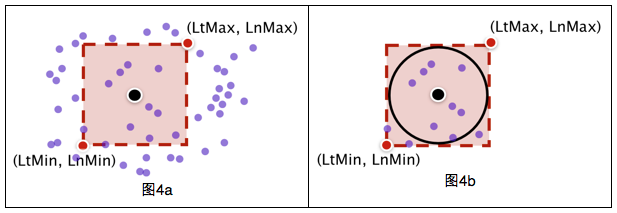
先用矩形框過濾(圖4a),判斷一個點在矩形框內很簡單,只要進行兩次判斷(LtMin<lat<LtMax; LnMin<lng<LnMax),落在矩形框內的POI個數為n(n<<40萬);
用球面距離公式計算位置與矩形框內n個POI的距離(圖4b),并保留距離小于50米的POI
矩形過濾方法的復雜度:40萬矩形過濾函數 + n距離函數(n<<40萬)。
根據這個思路我們執行SQl查詢(圖5)(注: 經度或緯度每隔0.001度,距離相差約100米,由此推算出矩形左下角和右上角坐標),發現過濾后正好剩下兩個POI。
此查詢花費了0.36秒,相比于方法一查詢時間大大降低,但是對于一次查詢來說還是很長。時間長的原因在于遍歷了40萬次。

方法二耗時的原因在于執行了遍歷操作,為了不進行遍歷,我們自然想到了索引。我們對緯度進行了B樹索引。
alter table poi_spatial add index latindex(lat);alter table poi_spatial add index lngindex(lng);
此方法包括三個步驟:
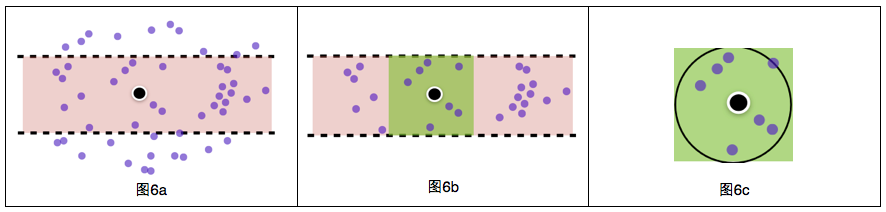
通過B樹快速找到某緯度范圍的POI(圖6a),個數為m(m<40萬),復雜度為Log(40萬)*過濾函數;
在步驟a過濾得到的m個POI中查找某經度范圍的POI(圖6b),個數為n(n<m),復雜度為m*過濾函數;
用球面距離公式計算位置與步驟b得到的n個POI的距離(圖6c),并保留距離小于50米的POI
執行SQL查詢(圖7),發現時間已經大大降低,從方法2的0.36秒下降到0.01秒

這時候有人會說了:方法三效果如此好,能夠滿足我們附近POI查詢問題啊,看來B樹用來索引空間數據也是可以的嘛!
那么B樹真的能夠索引空間數據嗎?
只能對經度或緯度索引(一維索引),與期望的不符
我們期待的是快速找出落在某一空間范圍的POI(如矩形)(圖8a),而不是快速找出落在某緯度或經度范圍的POI(圖8b),想象一下,我要查詢北京某區的POI,但是B樹索引不僅給我找出了北京的,還有與北京同一維度的天津、大同、甚至國外城市的POI,當數據量很大時,效率很低。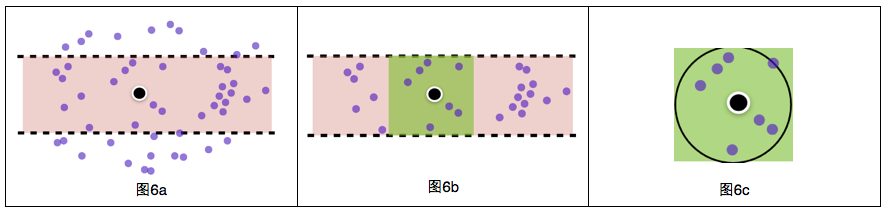
當數據是多維,比如三維(x,y,z),B樹怎么索引?
比如z可能是高程值,也可能是時間。有人會說B樹其實可以對多個字段進行索引,但這時需要指定優先級,形成一個組合字段,而空間數據在各個維度方向上不存在優先級,我們不能說緯度比經度更重要,也不能說緯度比高程更重要。
當空間數據不是點,而是線(道路、地鐵、河流等),面(行政區邊界、建筑物等),B樹怎么索引?
對于面來說,它由一系列首尾相連的經緯度坐標點組成,一個面可能有成百上千個坐標,這時數據庫怎么存儲,B樹怎么索引,這些都是問題。
既然傳統的索引不能很好的索引空間數據,我們自然需要一種方法能對空間數據進行索引,即空間索引。
SpringBoot + Redis 實現geo操作。
調用Java三方依賴判斷兩點距離
判斷 一個IP坐標是否在中國地圖內,核心思想就是看點到線上的交點看是否在右邊。具體看參考文檔實戰代碼。
看完上述內容,你們掌握如何進行Redis GeoHash核心原理解析的方法了嗎?如果還想學到更多技能或想了解更多相關內容,歡迎關注億速云行業資訊頻道,感謝各位的閱讀!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。