您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
這篇文章主要介紹“計算機中一個byte的存儲范圍是多少”,在日常操作中,相信很多人在計算機中一個byte的存儲范圍是多少問題上存在疑惑,小編查閱了各式資料,整理出簡單好用的操作方法,希望對大家解答”計算機中一個byte的存儲范圍是多少”的疑惑有所幫助!接下來,請跟著小編一起來學習吧!
我們知道,對于有符號類型,計算機在處理的時候會把最高位當做符號位,0表示正數,1表示負數。舉例來說(以下舉例均針對8位有符號數):
0000 0001即為1,1000 0001即為-1,那么很容易得到8位有符號數值的表示范圍應該是1111 1111 ~ 0111 1111,也就是-127~127,問題來了,-128是怎么來的呢?
在說明這個問題之前,先來補充點額外的知識:
在計算機的存儲和計算中,統一的是采用補碼進行處理和運算的,在弄清楚采用補碼的好處之前,我們需要明確如下三個概念:
原碼:是一種計算機中對數字的二進制定點表示方法。原碼表示法在數值前面增加了一位符號位(即最高位為符號位):正數該位為0,負數該位為1(0有兩種表示:+0和-0),其余位表示數值的大小。
反碼:正數的反碼與其原碼相同;負數的反碼是對其原碼逐位取反,但符號位除外。
補碼:正數的補碼與其原碼相同;負數的補碼等于其反碼+1。
很明顯,文章開頭的舉例即是原碼,它很符合我們的直觀感覺,但是在計算的時候麻煩就來了,如果直接運算,例如1+(-1)=0,運算的時候0000 0001 + 1000 0001 = 1000 0010(-2),很顯然是錯誤的,因此符號位和數值位必須分開處理!這會增加計算機的硬件開銷。我們換成補碼試試,1的原碼0000 0001,反碼0000 0001,補碼0000 0001(正數三者一致);-1的原碼1000 0001,反碼1111 1110,補碼1111 1111(1111 1110 + 0000 0001);因此1+(-1)用補碼來運算就是0000 0001 + 1111 11111 = 0000 0000(最高位溢出舍棄),結果是正確的。
由此可見,可以將減法運算轉化成加法運算,計算機只需要實現加法電路即可,并且原碼到補碼的轉換和補碼到原碼的轉換過程是完全一致的,為什么?可以簡單證明如下:
假設32位機器,X為負數(最高位是符號位,對于負數,即為1),則有X(絕對值)+X(反)=0xFFFFFFFFF,因此X(絕對值)+X(反)+1=0xFFFFFFFFF+1=0;所以得到 0-X(絕對值)=X(反)+1,根據之前的定義X(反)+1即為X的補碼,于是有X(補)=X(反)+1=0-X(絕對值);
1)那么對于A、B>0,令K=-B,顯然K是負數,那么有A-B=A+(0-K(絕對值))=A+K(補),減法運算就轉化成了加法運算。
2)X(絕對值)=0-X(補);兩邊同時乘以-1 得到-X(絕對值)=-0-(-X(補))=0-(X(補(絕對值)))=X(補)(反)+1;-X(絕對值)即為原碼X;因此上式說明了原碼X等于X的補碼取反后加一,也就是說X補碼的補碼就是原碼。不論是原碼求補碼還是補碼求原碼方式完全一致。
回到最開始的問題,8位有符號數值的最小值為什么是-128而不是-127呢,我們列出來部分原碼、反碼和補碼的對照表看看: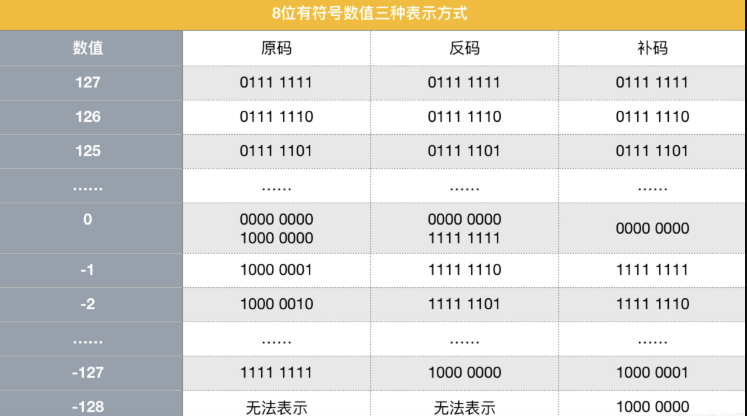
從上表中我們可以看出,0在原碼和反碼中有兩種表示方式,而對應的補碼只有一種表示方式,-128在原碼和反碼中無法表示,在補碼中卻可以表示(用-127的補碼1000 0001減1得到1000 0000)。而計算機中數值以補碼形式存儲和運算,當然-128可以表示出來,因此8位有符號數值的范圍是-128~127,同理其他位數(16、32、64)也可以以此類推。
說白了就是 在 -0 跟+0 的源碼 一個是 1000 0000 跟 0000 0000 這倆個是重復的,但是-0不要浪費了 跟補碼是一樣的 讓它表示-128也可以。
到此,關于“計算機中一個byte的存儲范圍是多少”的學習就結束了,希望能夠解決大家的疑惑。理論與實踐的搭配能更好的幫助大家學習,快去試試吧!若想繼續學習更多相關知識,請繼續關注億速云網站,小編會繼續努力為大家帶來更多實用的文章!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。