您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
這篇文章將為大家詳細講解有關浮點數的表示范圍是多少,文章內容質量較高,因此小編分享給大家做個參考,希望大家閱讀完這篇文章后對相關知識有一定的了解。
浮點數是由符號,階碼和尾數三部分組成,浮點數分為單精度浮點數和雙精度浮點數,單精度浮點數的便是范圍是-3.4E38~3.4E38,雙精度浮點數的范圍是-1.79E+308 ~ +1.79E+308
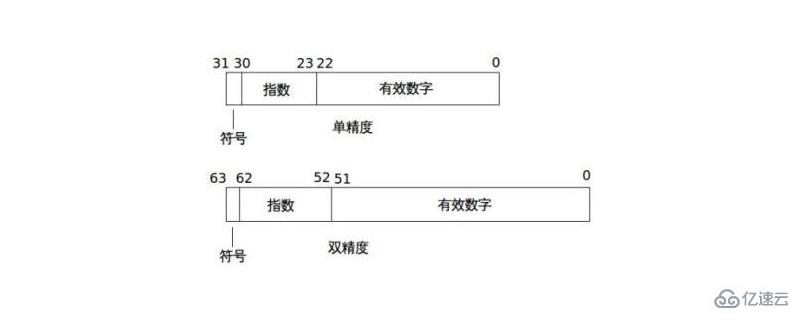
浮點數表示
一個浮點數(Floating Point Number)由三個基本成分構成:符號(Sign)、階碼(Exponent)和尾數(Mantissa)。通常可以用下面的格式來表示浮點數:
| S | P | M |
其中S是符號位,P是階碼,M是尾數。
根據IEEE(美國電氣和電子工程師學會)754標準中的定義,單精度浮點數是32位(即4字節)的,雙精度浮點數是64位(即8字節)的。兩者的S、P、M所占的位數以及表示方法由下表可知:
| S | P | M | 表示公式 | 偏移量 | |
| 單精度浮點數 | 1(第31位) | 8(30到23位) | 23(22到0位) | (-1)^S*2(P-127)*1.M | 127 |
| 雙精度浮點數 | 1(第63位) | 11(62到52位) | 52(51到0位) | (-1)^S*2(P-1023)*1.M | 1023 |
其中S是符號位,只有0和1,分別表示正負
P是階碼,通常使用移碼表示(移碼和補碼只有符號位相反,其余都一樣。對于正數而言,原碼、反碼和補碼都一樣;對于負數而言,補碼就是其絕對值的原碼全部取反,然后加1)。階碼可以為正數,也可以為負數,為了處理負指數的情況,實際的指數值按要求需要加上一個偏差(Bias)值作為保存在指數域中的值,單精度數的偏差值為127,雙精度數的偏差值為1023。例如,單精度的實際指數值0在指數域中將保存為127,而保存在指數域中的64則表示實際的指數值-63,偏差的引入使得對于單精度數,實際可以表達的指數值的范圍就變成-127到128之間(包含兩端)。
M為尾數,其中單精度數為23位長,雙精度數為52位長。IEEE標準要求浮點數必須是規范的。這意味著尾數的小數點左側必須為1,因此在保存尾數的時候,可以省略小數點前面這個1,從而騰出一個二進制位來保存更多的尾數。這樣實際上用23位長的尾數域表達了24位的尾數。例如對于單精度數而言,二進制的1001.101(對應于十進制的9.625)可以表達為1.001101 × 23,所以實際保存在尾數域中的值為00110100000000000000000,即去掉小數點左側的1,并用0在右側補齊。
根據標準要求,無法精確保存的值必須向最接近的可保存的值進行舍入,即不足一半則舍,一半以上(包括一半)則進。不過對于二進制浮點數而言,還多一條規矩,就是當需要舍入的值剛好是一半時,不是簡單地進,而是在前后兩個等距接近的可保存的值中,取其中最后一位有效數字為零者。
據以上分析,IEEE 754標準中定義浮點數的表示范圍為:
| 二進制(Binary) | 十進制(Decimal) | |
| 單精度浮點數 | ± (2-2^-23) × 2127 | ~ ± 10^38.53 |
| 雙精度浮點數 | ± (2-2^-52) × 21023 | ~ ± 10^308.25 |
浮點數的表示有一定的范圍,超出范圍時會產生溢出(Flow),一般稱大于絕對值最大的數據為上溢(Overflow),小于絕對值最小的數據為下溢(Underflow)。
浮點數的表示約定
單精度浮點數和雙精度浮點數都是用IEEE 754標準定義的,其中有一些特殊約定,例如:
1、當P=0,M=0時,表示0。
2、當P=255,M=0時,表示無窮大,用符號位來確定是正無窮大還是負無窮大。
3、當P=255,M≠0時,表示NaN(Not a Number,不是一個數)。
非規范浮點數
當兩個絕對值極小的浮點數相減后,其差值的指數可能超出允許范圍,最終只能近似為0。為了解決此類問題,IEEE標準中引入了非規范(Denormalized)浮點數,規定當浮點數的指數為允許的最小指數值時,尾數不必是規范化(Normalized)的。有了非規范浮點數,去掉了隱含的尾數位的制約,可以保存絕對值更小的浮點數。而且,由于不再受到隱含尾數域的制約,上述關于極小差值的問題也不存在了,因為所有可以保存的浮點數之間的差值同樣可以保存。
根據IEEE 754標準中的定義,規范和非規范浮點數的表示范圍可歸納為下表:
| 規范浮點數 | 非規范浮點數 | 十進制近似范圍 | |
| 單精度浮點數 | ± 2^-149 至 (1-2^-23)*2^-126 | ± 2^-126 至 (2-2^-23)*2^127 | ± ~10^-44.85 至 ~10^38.53 |
| 雙精度浮點數 | ± 2^-1074 至 (1-2^-52)*2^-1022 | ± 2^-1022 至 (2-2^-52)*2^1023 | ± ~10^-323.3 至 ~10^308.3 |
與IEEE 754相關的標準
本文的結論基于IEEE 754標準,另外一個標準是IEEE 854,這個標準是關于十進制浮點數的,但沒有規定具體格式,所以很少被采用。另外,從2000年開始,IEEE 754開始修訂,被稱為IEEE 754R,目的是融合IEEE 754和IEEE 854標準。該標準在浮點格式方面的修訂有:1、加入了16位和128位的二進制浮點數格式;2、加入了十進制浮點數格式,采用了IBM公司提出的格式。
關于浮點數的表示范圍是多少就分享到這里了,希望以上內容可以對大家有一定的幫助,可以學到更多知識。如果覺得文章不錯,可以把它分享出去讓更多的人看到。
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。