您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
這篇文章主要介紹“Java圖的遍歷怎么理解”,在日常操作中,相信很多人在Java圖的遍歷怎么理解問題上存在疑惑,小編查閱了各式資料,整理出簡單好用的操作方法,希望對大家解答”Java圖的遍歷怎么理解”的疑惑有所幫助!接下來,請跟著小編一起來學習吧!
圖的遍歷跟樹的遍歷一樣,從圖中一點出發遍歷圖中其余頂點,且使每一個頂點僅被訪問一次 叫 Traversing Graph
depth first search DFS 深度優先遍歷 深度優先搜索 類似與Tree中 前序遍歷
具體算法表述如下:
訪問初始結點v,并標記結點v為已訪問。
查找結點v的第一個鄰接結點w。
若w存在,則繼續執行4,否則算法結束。
若w未被訪問,對w進行深度優先遍歷遞歸(即把w當做另一個v,然后進行步驟123)。
查找結點v的w鄰接結點的下一個鄰接結點,轉到步驟3。
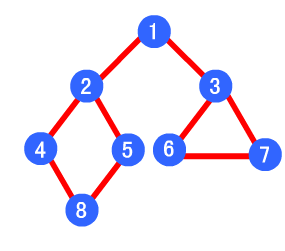
例如下圖,其深度優先遍歷順序為 1->2->4->8->5->3->6->7
bool visited[MAX];//初始化全為false
鄰接矩陣 深度優化遞歸 因為邊存在1才能訪問
// 遞歸法
void DFS(MGraph G, int i)//從第i個開始遍歷
{
visited[i] = true;
cout<<G.VexArr[i];
for(int j=0;j<G.numV;j++)
{
if(G.arc[i][j] == 1 && ! visited[j])
{
DFS(G,j);
}
}
}
void DFSTraverse(MGraph G) //鄰接矩陣深度遍歷操作
{
for(int i=0;i<G.numV;j++)
{
visited[i] = false;
}
for(int i=0;i<G.numV;i++)
{
if(! visited[i])//對未訪問過的頂點調用DFS, 如果是連通圖則上面的for循環只執行一次就
{
DFS(G,i);
}
}
}
鄰接表
bool visited[MAX];//初始化全為false
鄰接表 深度優化遞歸
// 遞歸法
void DFS(GraphList G, int i)//從第i個開始遍歷
{
visited[i] = true;
EdgeNode *p = NULL;
cout << G.adjlist[i].data;//輸出 剛剛遍歷的那個節點
p = G->adjlist[i].firstedge;//p指向 鄰接表的首地址
while(p)
{
if(!visited[p->adjvex])
{
DFS(G, p->adjvex);
}
p = p->next;
}
}
void DFSTraverse(GraphList G) //鄰接矩陣深度遍歷操作
{
for(int i=0;i<G.numV;j++)
{
visited[i] = false;
}
for(int i=0;i<G.numV;i++)
{
if(! visited[i])//對未訪問過的頂點調用DFS, 如果是連通圖則上面的for循環只執行一次就
{
DFS(G,i);
}
}
}對于n個頂點e個邊的圖來說 鄰接矩陣遍歷時間復雜度為O(n^2); 而鄰接表復雜度為O(n+e); 對于有向圖而言只是在對通道存在可行或者不可行,基本算法上差別不太大
到此,關于“Java圖的遍歷怎么理解”的學習就結束了,希望能夠解決大家的疑惑。理論與實踐的搭配能更好的幫助大家學習,快去試試吧!若想繼續學習更多相關知識,請繼續關注億速云網站,小編會繼續努力為大家帶來更多實用的文章!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。