數據庫鄰接表有什么特點

本篇內容介紹了“數據庫鄰接表有什么特點”的有關知識，在實際案例的操作過程中，不少人都會遇到這樣的困境，接下來就讓小編帶領大家學習一下如何處理這些情況吧！希望大家仔細閱讀，能夠學有所成！

2. 鄰接表（無向圖）的特點：

有時候鄰接矩陣并不是一個很好的選擇：

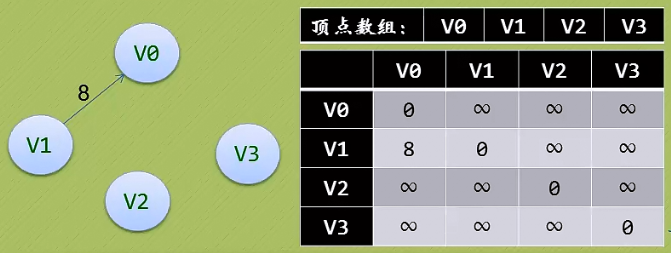
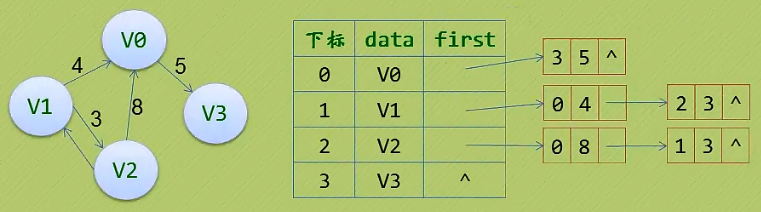
如上圖： 邊數相對頂點較少，這種結構無疑是存在對存儲空間的極大浪費。

鄰接表： 數組和鏈表結合一起來存儲。

1.）頂點用一個一位數組存儲。

2.）每個頂點Vi的所有鄰接點構成一個線性表，由于鄰接點的個數不確定，所以我們選擇單鏈表來存儲。

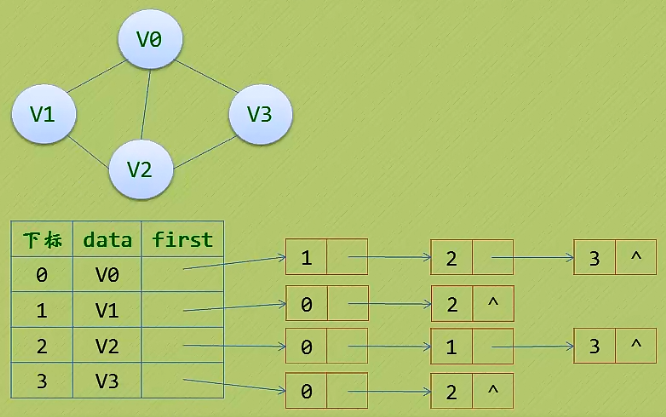
2. 鄰接表（有向圖）的特點：

把頂點當弧尾建立的鄰接表，這樣很容易就可以得到每個頂點的出度。

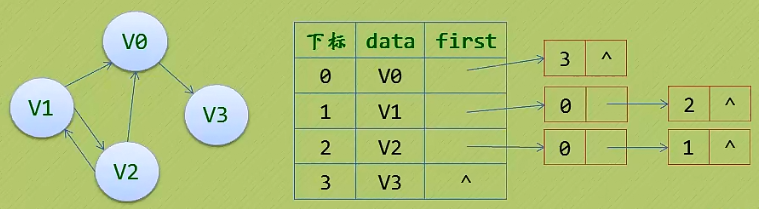
有時為了便于確定頂點的入度或以頂點為弧頭的弧，我們可以建立一個有向圖的逆鄰接表：

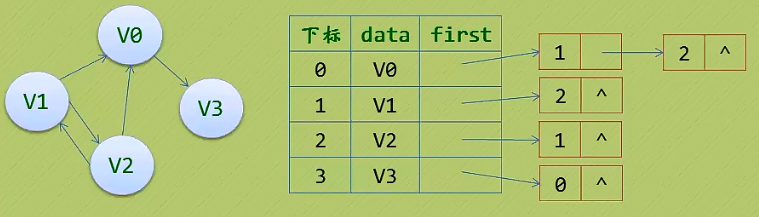
3. 鄰接表（網）的特點：

對于帶權值的網圖，可以在邊表結點定義中再增加一個數據域來存儲權值即可：

typedef char Vtype //頂點類型
typedef int Etype //權值類型
#definde MAXV 100;
typedef struct edgeNode //邊表節點
{
	int adjvex; //鄰接點 存儲該頂點對應的下標
	Etype weight;//邊 權值
	struct edgeNode *next;
}EdgeNode;

typedef struct Vnode //頂點表 節點
{
	Vtype data;
	EdgeNode* firstEdge;
}VNODE; //

typedef struct
{
	VNODE adjlist[MAXV];
	int numV;//當前頂點數
	int numE;//當前邊數
}GraphAdjList;  

void CreateALGraph(GraphAdjList* G)
{
	int i,j,k;
	EdgeNode* e= NULL;
	cout<<輸入頂點數";
	cin>>G->numV;
	cout<<輸入邊數";
	cin>>G->numE;
	for(i=0;i<G->numV;i++)//建立頂點信息
	{
		cin >> G->adjlist[i].data; //輸入頂點信息
		G->adjlist[i].firstEdge = NULL; //邊表節點 為空
	}
	for(k=0;k<numE;k++)//建立邊信息
	{
		cout<<"輸入邊的開始";  
		cin>>i;  
		cout<<"輸入邊的結尾";  
		cin>>j;
		
		e = new EdgeNode; //(1,3) 這個線的插入是相互的對于兩個點1,3來說 分別不同的因此有兩個new
		e->adjvex = j;
		e->next = G->adjlist[i].firstEdge; //類似與棧里的 node->next = list->head;  list->head = node;
		G->adjlist[i].firstEdge = e;
		
		e = new EdgeNode;
		e->adjvex = i;
		e->next = G->adjlist[j].firstEdge;
		G->adjlist[j].firstEdge = e;
	}
}

對于無向圖來說一條邊對應都是兩個頂點，所以在一次循環中就對i和j分別進行了插入  對于n個頂點e個邊來說 O(n+e)

“數據庫鄰接表有什么特點”的內容就介紹到這里了，感謝大家的閱讀。如果想了解更多行業相關的知識可以關注億速云網站，小編將為大家輸出更多高質量的實用文章！