您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
這篇文章給大家介紹比特幣ECDSA與Schnorr簽名算法及Taproot的升級是怎樣的,內容非常詳細,感興趣的小伙伴們可以參考借鑒,希望對大家能有所幫助。
2020 年 1 月,由比特幣核心開發人員 Pieter Wuille 于去年 5 月提出的 Taproot/Schnorr 軟分叉升級提案已正式作為比特幣改進提案(BIPs)發布,相關提案序號為 BIP 340-342。Taproot/Schnorr 升級如果獲得社區支持,將是比特幣自閃電網絡上線后最大的技術拓展。本文查詢了 BIP 340-342 相關文檔 ,對 Taproot/Schnorr 升級做一個簡單介紹。本文分三部分,第一部分簡單介紹比特幣目前的 ECDSA 簽名算法,第二部分詳細介紹 Schnorr 簽名算法,第三部分介紹 Taproot。
比特幣目前使用的 ECDSA 簽名算法與建議的 Schnorr 簽名算法,都屬于橢圓曲線數字簽名算法,它們使用的橢圓曲線都是 secp256k1。這一部分先介紹橢圓曲線 secp256k1,再介紹 ECDSA 簽名算法。



注: G 坐標為
(79BE667EF9DCBBAC55A06295CE870B07029BFCDB2DCE28D959F2815B16F81798, 483ADA7726A3C4655DA4FBFC0E1108A8FD17B448A68554199C47D08FFB10D4B8),
階等于
FFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEBAAEDCE6AF48A03BBFD25E8CD0364141,
均采用 16 進制表達。

這一部分先介紹 Schnorr 簽名算法主要特點,再分步驟介紹 Schnorr 簽名算法及批驗證,最后介紹基于 Schnorr 簽名的多重簽名算法。
Schnorr 簽名算法與 ECDSA 簽名算法使用同樣的橢圓曲線 secp256k1 和哈希函數 SHA256,所以在這個層面它們具有同樣的安全性。Schnorr 簽名算法主要有以下優點。
第一,Schnorr 簽名算法有可證明安全性。在假設橢圓曲線離散對數問題難度的隨機寓言(Random Oracle)模型,以及假設原像抗性(Preimage Resistance)和次原像抗性(Second Preimage Resistance)的通用群模型下,Schnorr 簽名算法具備選擇消息攻擊下的強不可偽造性(Strong Unforgeability under Chosen Message Attack,SUF-CMA)。換言之,如果不知道 Schnorr 簽名的私鑰,即使有針對任意消息的有效 Schnorr 簽名,也沒法推導出其他有效 Schnorr 簽名。而 ECDSA 簽名算法的可證明安全性則依賴于更強的假設。
第二,Schnorr 簽名算法具有不可延展性(Non-malleability)。簽名延展性的含義是,第三方在不知道私鑰的情況下,能將針對某一公鑰和消息的有效簽名,改造成針對該公鑰和信息的另一個有效簽名。ECDSA 簽名算法則有內在的可延展性,這是 BIP 62 和 BIP 146 針對的問題。
第三,Schnorr 簽名算法是線性的,使得多個合作方能生成對他們的公鑰之和也有效的簽名。這一特點對多重簽名、批驗證(Batch Verification)等應用非常重要,既能提高效率,也有助于保護隱私。而在 ECDSA 簽名算法下,如無額外的見證數據,批驗證相對逐個驗證并無效率提升。
最后,Schnorr 簽名算法因為使用同樣的橢圓曲線 secp256k1 和哈希函數 SHA256,能兼容目前的比特幣公私鑰生成機制。



批驗證
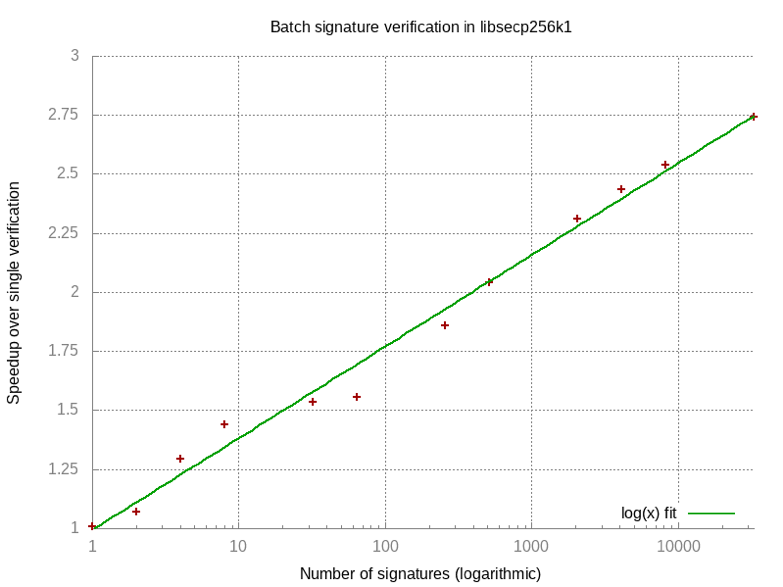
圖 2:逐個驗證簽名的時間 / 批驗證所需時間

簽名生成

Taproot 升級可以視為默克抽象語言樹(Merkelized Abstract Syntax Tree,簡稱 MAST)的一個應用,而 MAST 又與支付到腳本哈希(Pay-to-Script-Hash,簡稱 P2SH)有關。因此,這部分依次介紹 P2SH、MAST 和 Taproot。
P2SH 是 2012 年推出的一類新型交易,使復雜腳本的使用與直接向比特幣地址支付一樣簡單。在 P2SH 中,復雜的鎖定腳本被其哈希值所取代,稱為兌換腳本(Redeem Script)。當隨后出現的一筆交易試圖花費這個 UTXO 時,必須包含與哈希值匹配的腳本,同時解鎖腳本。P2SH 的主要優點包括:一是在交易輸出中,復雜腳本由哈希值取代,使得交易代碼變短。二是將構建腳本的負擔轉移至接收方,而非發送方。三是隱私保護性更好。理論上,除了接收方,任何其他方都可以不知道兌換腳本中包含的支出條件。比如,在多重交易中,發送方可以不知道與多重簽名地址有關的公鑰;只在接收方支出資金時,才披露公鑰。但 P2SH 也存在不足:一是所有可能的支出條件最終都必須被披露,包括那些實際上沒有被觸發的支出條件。二是在有多個可能的支出條件時,P2SH 將變得繁復,會增加計算和驗證的工作量。
MAST 使用默克樹來加密復雜的鎖定腳本(圖 3),其葉子是一系列相互不重疊的腳本(比如,多重簽名或時間鎖)。要支出時,只需披露相關腳本以及從該腳本通向默克樹根的路徑。比如,在圖 3 中,要使用 script 1,只需披露 script 1、script 2 以及 hash 3 即可。
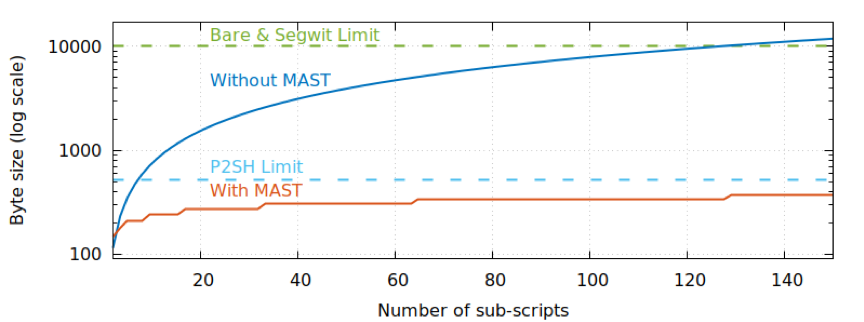
圖 4:腳本數量與交易大小,來源:https://bitcointechtalk.com/what-is-a-bitcoin-merklized-abstract-syntax-tree-mast-33fdf2da5e2f
但 P2SH 與常見的支付到公鑰哈希(Pay-to-Public-Key-Hash,P2PKH)在表現上不一樣,仍然有隱私保護問題。有沒有可能讓 P2SH 和 P2PKH 在鏈上看起來一樣?這就是 Taproot 要解決的問題。
涉及有限數量簽名者的腳本,可以分解成兩部分:第一部分是多重簽名,所有簽名者都同意某一支出結果,稱為「協作式支出」;第二部分稱為「非協作式支出」,可以有非常復雜的腳本結構。這兩部分是「或」的關系。比如,在圖 3 中,Script 3 是一個 2-of-2 型多重簽名,需要 Alice 和 Bob 兩人都簽名才有效,是「協作式支出」;Script 1 和 2 是「非協作式支出」。

關于比特幣ECDSA與Schnorr簽名算法及Taproot的升級是怎樣的就分享到這里了,希望以上內容可以對大家有一定的幫助,可以學到更多知識。如果覺得文章不錯,可以把它分享出去讓更多的人看到。
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。