KMeans算法原理及Spark實現是怎樣的

這篇文章給大家介紹KMeans算法原理及Spark實現是怎樣的，內容非常詳細，感興趣的小伙伴們可以參考借鑒，希望對大家能有所幫助。

1. KMeans - 算法簡介

K-Means算法是無監督的聚類算法，它實現起來比較簡單，聚類效果也不錯，因此應用很廣泛，

• K-means算法，也稱為K-平均或者K-均值，一般作為掌握聚類算法的第一個算法。

• 這里的K為常數，需事先設定，通俗地說該算法是將沒有標注的 M 個樣本通過迭代的方式聚集成K個簇。

• 在對樣本進行聚集的過程往往是以樣本之間的距離作為指標來劃分。

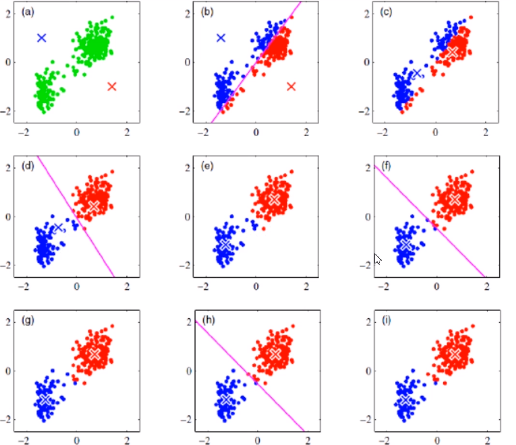核心：K-means聚類算法是一種迭代求解的聚類分析算法，其步驟是隨機選取K個對象作為初始的聚類中心，然后計算每個對象與各個種子聚類中心之間的距離，把每個對象分配給距離它最近的聚類中心。聚類中心以及分配給它們的對象就代表一個聚類。每分配一個樣本，聚類的聚類中心會根據聚類中現有的對象被重新計算。這個過程將不斷重復直到滿足某個終止條件。終止條件可以是沒有（或最小數目）對象被重新分配給不同的聚類，沒有（或最小數目）聚類中心再發生變化，誤差平方和局部最小

2.KMeans 算法流程

2.1 讀取文件，準備數據，對數據進行預處理

2.2 隨機找K個點，作為初始的中心點

2.3 遍歷數據集，計算每一個點到3個中心的距離，距離那個中心點最近就屬于哪個中心點

2.4 根據新的分類計算新的中心點

2.5 使用新的中心點開始下一次循環（繼續循環步驟2.3）

退出循環的條件：

1.指定循環次數

2.所有的中心點幾乎不再移動（即中心點移動的距離總和小于我們給定的一個常熟，比如0.00001）

3. KMeans算法優缺點

K值的選擇： k 值對最終結果的影響至關重要，而它卻必須要預先給定。給定合適的 k 值，需要先驗知識，憑空估計很困難，或者可能導致效果很差。

異常點的存在：K-means算法在迭代的過程中使用所有點的均值作為新的質點(中心點)，如果簇中存在異常點，將導致均值偏差比較嚴重。 比如一個簇中有2、4、6、8、100五個數據，那么新的質點為24，顯然這個質點離絕大多數點都比較遠；在當前情況下，使用中位數6可能比使用均值的想法更好，使用中位數的聚類方式叫做K-Mediods聚類(K中值聚類)

初值敏感：K-means算法是初值敏感的，選擇不同的初始值可能導致不同的簇劃分規則。為了避免這種敏感性導致的最終結果異常性，可以采用初始化多套初始節點構造不同的分類規則，然后選擇最優的構造規則。針對這點后面因此衍生了：二分K-Means算法、K-Means++算法、K-Means||算法、Canopy算法等

實現簡單、移動、伸縮性良好等優點使得它成為聚類中最常用的算法之一。

4.KMeans算法Spark實現

4.1 數據下載和說明

鏈接：https://pan.baidu.com/s/1FmFxSrPIynO3udernLU0yQ提取碼：hell 復制這段內容后打開百度網盤手機App，操作更方便哦

鳶尾花數據集，數據集包含3類共150調數據，每類含50個數據，每條記錄含4個特征：花萼長度、花萼寬度、花瓣長度、花瓣寬度

過這4個 特征，將花聚類，假設將K取值為3，看看與實際結果的差別

4.2 實現

沒有使用mlb庫，而是使用scala原生實現

package com.hoult.work

import org.apache.commons.lang3.math.NumberUtils
import org.apache.spark.SparkContext
import org.apache.spark.rdd.RDD
import org.apache.spark.sql.SparkSession

import scala.collection.mutable.ListBuffer
import scala.math.{pow, sqrt}
import scala.util.Random

object KmeansDemo {

  def main(args: Array[String]): Unit = {

    val spark = SparkSession
      .builder()
      .master("local[*]")
      .appName(this.getClass.getCanonicalName)
      .getOrCreate()

    val sc = spark.sparkContext
    val dataset = spark.read.textFile("data/lris.csv")
      .rdd.map(_.split(",").filter(NumberUtils.isNumber _).map(_.toDouble))
      .filter(!_.isEmpty).map(_.toSeq)


    val res: RDD[(Seq[Double], Int)] = train(dataset, 3)

    res.sample(false, 0.1, 1234L)
      .map(tp => (tp._1.mkString(","), tp._2))
      .foreach(println)
  }

  // 定義一個方法 傳入的參數是 數據集、K、最大迭代次數、代價函數變化閾值
  // 其中 最大迭代次數和代價函數變化閾值是設定了默認值，可以根據需要做相應更改
  def train(data: RDD[Seq[Double]], k: Int, maxIter: Int = 40, tol: Double = 1e-4) = {

    val sc: SparkContext = data.sparkContext

    var i = 0 // 迭代次數
    var cost = 0D //初始的代價函數
    var convergence = false   //判斷收斂，即代價函數變化小于閾值tol

    // step1 :隨機選取 k個初始聚類中心
    var initk: Array[(Seq[Double], Int)] = data.takeSample(false, k, Random.nextLong()).zip(Range(0, k))

    var res: RDD[(Seq[Double], Int)] = null

    while (i < maxIter && !convergence) {

      val bcCenters = sc.broadcast(initk)

      val centers: Array[(Seq[Double], Int)] = bcCenters.value

      val clustered: RDD[(Int, (Double, Seq[Double], Int))] = data.mapPartitions(points => {

        val listBuffer = new ListBuffer[(Int, (Double, Seq[Double], Int))]()

        // 計算每個樣本點到各個聚類中心的距離
        points.foreach { point =>

          // 計算聚類id以及最小距離平方和、樣本點、1
          val cost: (Int, (Double, Seq[Double], Int)) = centers.map(ct => {

            ct._2 -> (getDistance(ct._1.toArray, point.toArray), point, 1)

          }).minBy(_._2._1)  // 將該樣本歸屬到最近的聚類中心
          listBuffer.append(cost)
        }

        listBuffer.toIterator
      })
      //
      val mpartition: Array[(Int, (Double, Seq[Double]))] = clustered
        .reduceByKey((a, b) => {
          val cost = a._1 + b._1   //代價函數
          val count = a._3 + b._3   // 每個類的樣本數累加
          val newCenters = a._2.zip(b._2).map(tp => tp._1 + tp._2)    // 新的聚類中心點集
          (cost, newCenters, count)
        })
        .map {
          case (clusterId, (costs, point, count)) =>
            clusterId -> (costs, point.map(_ / count))   // 新的聚類中心
        }
        .collect()
      val newCost = mpartition.map(_._2._1).sum   // 代價函數
      convergence =  math.abs(newCost - cost) <= tol    // 判斷收斂，即代價函數變化是否小于小于閾值tol
      // 變換新的代價函數
      cost = newCost
      // 變換初始聚類中心
      initk = mpartition.map(tp => (tp._2._2, tp._1))
      // 聚類結果 返回樣本點以及所屬類的id
      res = clustered.map(tp=>(tp._2._2,tp._1))
      i += 1
    }
    // 返回聚類結果
    res
  }

  def getDistance(x:Array[Double],y:Array[Double]):Double={
    sqrt(x.zip(y).map(z=>pow(z._1-z._2,2)).sum)
  }


}

完整代碼：https://github.com/hulichao/bigdata-spark/blob/master/src/main/scala/com/hoult/work/KmeansDemo.scala

結果截圖：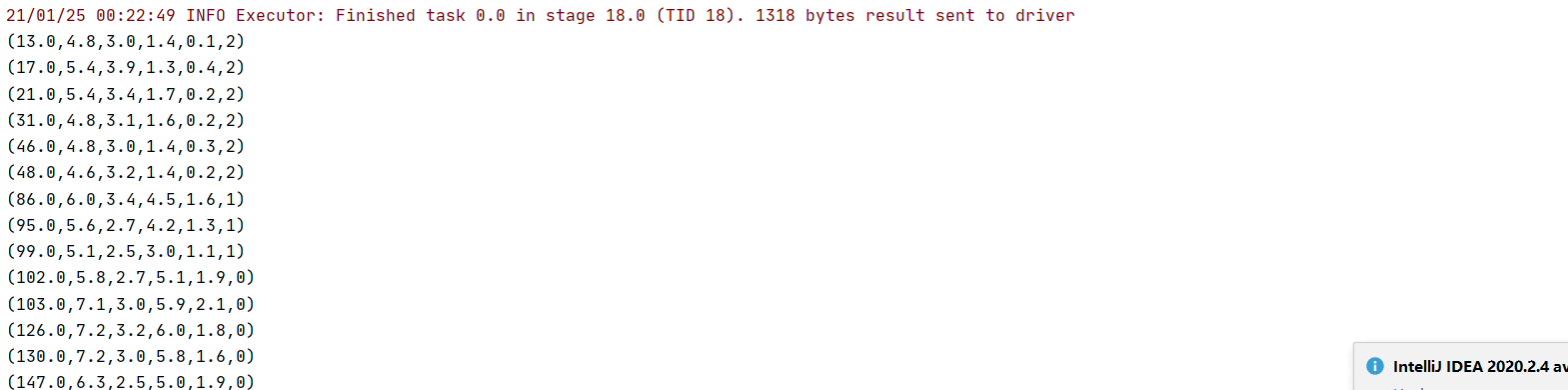

關于KMeans算法原理及Spark實現是怎樣的就分享到這里了，希望以上內容可以對大家有一定的幫助，可以學到更多知識。如果覺得文章不錯，可以把它分享出去讓更多的人看到。