如何分析python中二叉搜索樹的 AVL樹

今天就跟大家聊聊有關如何分析python中二叉搜索樹的 AVL樹，可能很多人都不太了解，為了讓大家更加了解，小編給大家總結了以下內容，希望大家根據這篇文章可以有所收獲。

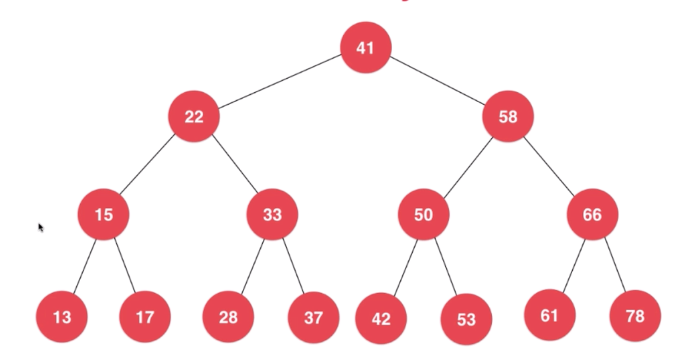
二分搜索樹 遞歸實現

public void add(E e){        root = add(root,e);    }        /**     * 二分搜索樹插入元素 遞歸實現     */    private Node add(Node node ,E e){        if (node==null){            size++;            return new Node(e);        }        if (e.compareTo(node.data)<0){           node.left = add(node.left,e);        }else if (e.compareTo(node.data)>0){            node.right = add(node.right,e);        }        return node;    }

二分搜索樹 查找遞歸實現

public boolean contains(E e){        return contains(root, e);    }    private boolean contains(Node node,E e){        if (node==null){            return false;        }if (e.compareTo(node.data)==0){            return true;        }else if(e.compareTo(node.data)<0){            return contains(node.left,e);        }else {            return contains(node.right,e);        }    }

二叉搜索樹一定程度上可以提高搜索效率，但是當原序列有序時，例如序列 A = {1，2，3，4，5，6}，構造二叉搜索樹如圖 1.1。依據此序列構造的二叉搜索樹為右斜樹，同時二叉樹退化成單鏈表，搜索效率降低為 O(n)。

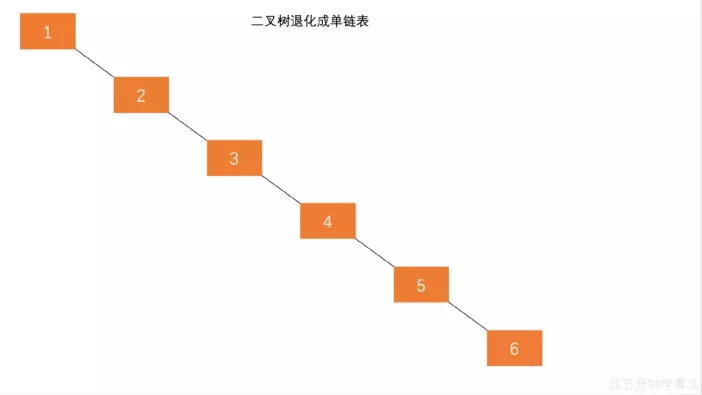
二叉搜索樹的查找效率取決于樹的高度，因此保持樹的高度最小，即可保證樹的查找效率。

概念

平衡二叉查找樹：簡稱平衡二叉樹。由前蘇聯的數學家 Adelse-Velskil 和 Landis 在 1962 年提出的高度平衡的二叉樹，根據科學家的英文名也稱為 AVL 樹。它具有如下幾個性質：

1. 可以是空樹。
   

2. 假如不是空樹，任何一個節點的左子樹與右子樹都是平衡二叉樹，并且高度之差的絕對值不超過 1。

看完上述內容，你們對如何分析python中二叉搜索樹的 AVL樹有進一步的了解嗎？如果還想了解更多知識或者相關內容，請關注億速云行業資訊頻道，感謝大家的支持。