Javascript常見數據結構的實現方法是什么

這篇文章主要講解了“Javascript常見數據結構的實現方法是什么”，文中的講解內容簡單清晰，易于學習與理解，下面請大家跟著小編的思路慢慢深入，一起來研究和學習“Javascript常見數據結構的實現方法是什么”吧！

1. Stack(棧)

Stack的特點是后進先出(last in first  out)。生活中常見的Stack的例子比如一摞書，你最后放上去的那本你之后會最先拿走;又比如瀏覽器的訪問歷史，當點擊返回按鈕，最后訪問的網站最先從歷史記錄中彈出。

1. Stack一般具備以下方法：

2. push：將一個元素推入棧頂

3. pop：移除棧頂元素，并返回被移除的元素

4. peek：返回棧頂元素

5. length：返回棧中元素的個數

Javascript的Array天生具備了Stack的特性，但我們也可以從頭實現一個 Stack類：

function Stack() {   this.count = 0;   this.storage = {};    this.push = function (value) {     this.storage[this.count] = value;     this.count++;   }    this.pop = function () {     if (this.count === 0) {       return undefined;     }     this.count--;     var result = this.storage[this.count];     delete this.storage[this.count];     return result;   }    this.peek = function () {     return this.storage[this.count - 1];   }    this.size = function () {     return this.count;   } }

2. Queue(隊列)

Queue和Stack有一些類似，不同的是Stack是先進后出，而Queue是先進先出。Queue在生活中的例子比如排隊上公交，排在第一個的總是最先上車;又比如打印機的打印隊列，排在前面的最先打印。

• Queue一般具有以下常見方法：

• enqueue：入列，向隊列尾部增加一個元素

• dequeue：出列，移除隊列頭部的一個元素并返回被移除的元素

• front：獲取隊列的第一個元素

• isEmpty：判斷隊列是否為空

• size：獲取隊列中元素的個數

Javascript中的Array已經具備了Queue的一些特性，所以我們可以借助Array實現一個Queue類型：

function Queue() {   var collection = [];    this.print = function () {     console.log(collection);   }    this.enqueue = function (element) {     collection.push(element);   }    this.dequeue = function () {     return collection.shift();   }    this.front = function () {     return collection[0];   }    this.isEmpty = function () {     return collection.length === 0;   }    this.size = function () {     return collection.length;   } }

Priority Queue(優先隊列)

Queue還有個升級版本，給每個元素賦予優先級，優先級高的元素入列時將排到低優先級元素之前。區別主要是enqueue方法的實現：

function PriorityQueue() {    ...    this.enqueue = function (element) {     if (this.isEmpty()) {       collection.push(element);     } else {       var added = false;       for (var i = 0; i < collection.length; i++) {         if (element[1] < collection[i][1]) {           collection.splice(i, 0, element);           added = true;           break;         }       }       if (!added) {         collection.push(element);       }     }   } }

測試一下：

var pQ = new PriorityQueue();  pQ.enqueue(['gannicus', 3]); pQ.enqueue(['spartacus', 1]); pQ.enqueue(['crixus', 2]); pQ.enqueue(['oenomaus', 4]);  pQ.print();

結果：

[   [ 'spartacus', 1 ],   [ 'crixus', 2 ],   [ 'gannicus', 3 ],   [ 'oenomaus', 4 ] ]

3. Linked List(鏈表)

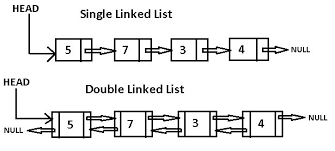
顧名思義，鏈表是一種鏈式數據結構，鏈上的每個節點包含兩種信息：節點本身的數據和指向下一個節點的指針。鏈表和傳統的數組都是線性的數據結構，存儲的都是一個序列的數據，但也有很多區別，如下表：

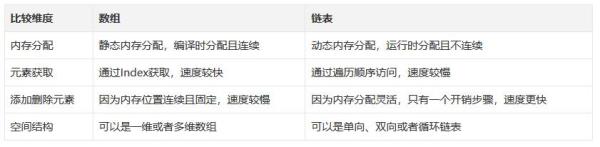
一個單向鏈表通常具有以下方法：

1. size：返回鏈表中節點的個數

2. head：返回鏈表中的頭部元素

3. add：向鏈表尾部增加一個節點

4. remove：刪除某個節點

5. indexOf：返回某個節點的index

6. elementAt：返回某個index處的節點

7. addAt：在某個index處插入一個節點

8. removeAt：刪除某個index處的節點

單向鏈表的Javascript實現：

/**  * 鏈表中的節點   */ function Node(element) {   // 節點中的數據   this.element = element;   // 指向下一個節點的指針   this.next = null; }  function LinkedList() {   var length = 0;   var head = null;    this.size = function () {     return length;   }    this.head = function () {     return head;   }    this.add = function (element) {     var node = new Node(element);     if (head == null) {       head = node;     } else {       var currentNode = head;        while (currentNode.next) {         currentNode = currentNode.next;       }        currentNode.next = node;     }     length++;   }    this.remove = function (element) {     var currentNode = head;     var previousNode;     if (currentNode.element === element) {       head = currentNode.next;     } else {       while (currentNode.element !== element) {         previousNode = currentNode;         currentNode = currentNode.next;       }       previousNode.next = currentNode.next;     }     length--;   }    this.isEmpty = function () {     return length === 0;   }    this.indexOf = function (element) {     var currentNode = head;     var index = -1;     while (currentNode) {       index++;       if (currentNode.element === element) {         return index;       }       currentNode = currentNode.next;     }      return -1;   }    this.elementAt = function (index) {     var currentNode = head;     var count = 0;     while (count < index) {       count++;       currentNode = currentNode.next;     }     return currentNode.element;   }    this.addAt = function (index, element) {     var node = new Node(element);     var currentNode = head;     var previousNode;     var currentIndex = 0;      if (index > length) {       return false;     }      if (index === 0) {       node.next = currentNode;       head = node;     } else {       while (currentIndex < index) {         currentIndex++;         previousNode = currentNode;         currentNode = currentNode.next;       }       node.next = currentNode;       previousNode.next = node;     }     length++;   }    this.removeAt = function (index) {     var currentNode = head;     var previousNode;     var currentIndex = 0;     if (index < 0 || index >= length) {       return null;     }     if (index === 0) {       head = currentIndex.next;     } else {       while (currentIndex < index) {         currentIndex++;         previousNode = currentNode;         currentNode = currentNode.next;       }       previousNode.next = currentNode.next;     }     length--;     return currentNode.element;   } }

4. Set(集合)

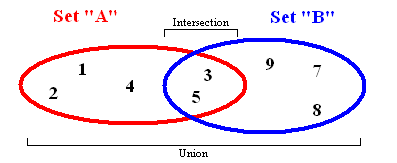
集合是數學中的一個基本概念，表示具有某種特性的對象匯總成的集體。在ES6中也引入了集合類型Set，Set和Array有一定程度的相似，不同的是Set中不允許出現重復的元素而且是無序的。

一個典型的Set應該具有以下方法：

1. values：返回集合中的所有元素

2. size：返回集合中元素的個數

3. has：判斷集合中是否存在某個元素

4. add：向集合中添加元素

5. remove：從集合中移除某個元素

6. union：返回兩個集合的并集

7. intersection：返回兩個集合的交集

8. difference：返回兩個集合的差集

9. subset：判斷一個集合是否為另一個集合的子集

使用Javascript可以將Set進行如下實現，為了區別于ES6中的Set命名為MySet：

function MySet() {   var collection = [];   this.has = function (element) {     return (collection.indexOf(element) !== -1);   }    this.values = function () {     return collection;   }    this.size = function () {     return collection.length;   }    this.add = function (element) {     if (!this.has(element)) {       collection.push(element);       return true;     }     return false;   }    this.remove = function (element) {     if (this.has(element)) {       index = collection.indexOf(element);       collection.splice(index, 1);       return true;     }     return false;   }    this.union = function (otherSet) {     var unionSet = new MySet();     var firstSet = this.values();     var secondSet = otherSet.values();     firstSet.forEach(function (e) {       unionSet.add(e);     });     secondSet.forEach(function (e) {       unionSet.add(e);     });     return unionSet;   }    this.intersection = function (otherSet) {     var intersectionSet = new MySet();     var firstSet = this.values();     firstSet.forEach(function (e) {       if (otherSet.has(e)) {         intersectionSet.add(e);       }     });     return intersectionSet;   }    this.difference = function (otherSet) {     var differenceSet = new MySet();     var firstSet = this.values();     firstSet.forEach(function (e) {       if (!otherSet.has(e)) {         differenceSet.add(e);       }     });     return differenceSet;   }    this.subset = function (otherSet) {     var firstSet = this.values();     return firstSet.every(function (value) {       return otherSet.has(value);     });   } }

5. Hash Table(哈希表/散列表)

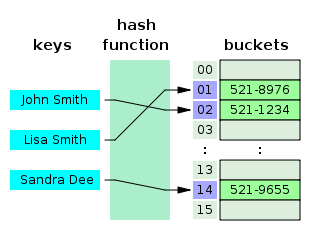
Hash Table是一種用于存儲鍵值對(key value pair)的數據結構，因為Hash  Table根據key查詢value的速度很快，所以它常用于實現Map、Dictinary、Object等數據結構。如上圖所示，Hash  Table內部使用一個hash函數將傳入的鍵轉換成一串數字，而這串數字將作為鍵值對實際的key，通過這個key查詢對應的value非常快，時間復雜度將達到O(1)。Hash函數要求相同輸入對應的輸出必須相等，而不同輸入對應的輸出必須不等，相當于對每對數據打上唯一的指紋。

一個Hash Table通常具有下列方法：

1. add：增加一組鍵值對

2. remove：刪除一組鍵值對

3. lookup：查找一個鍵對應的值

一個簡易版本的Hash Table的Javascript實現：

function hash(string, max) {   var hash = 0;   for (var i = 0; i < string.length; i++) {     hash += string.charCodeAt(i);   }   return hash % max; }  function HashTable() {   let storage = [];   const storageLimit = 4;    this.add = function (key, value) {     var index = hash(key, storageLimit);     if (storage[index] === undefined) {       storage[index] = [         [key, value]       ];     } else {       var inserted = false;       for (var i = 0; i < storage[index].length; i++) {         if (storage[index][i][0] === key) {           storage[index][i][1] = value;           inserted = true;         }       }       if (inserted === false) {         storage[index].push([key, value]);       }     }   }    this.remove = function (key) {     var index = hash(key, storageLimit);     if (storage[index].length === 1 && storage[index][0][0] === key) {       delete storage[index];     } else {       for (var i = 0; i < storage[index]; i++) {         if (storage[index][i][0] === key) {           delete storage[index][i];         }       }     }   }    this.lookup = function (key) {     var index = hash(key, storageLimit);     if (storage[index] === undefined) {       return undefined;     } else {       for (var i = 0; i < storage[index].length; i++) {         if (storage[index][i][0] === key) {           return storage[index][i][1];         }       }     }   } }

6. Tree(樹)

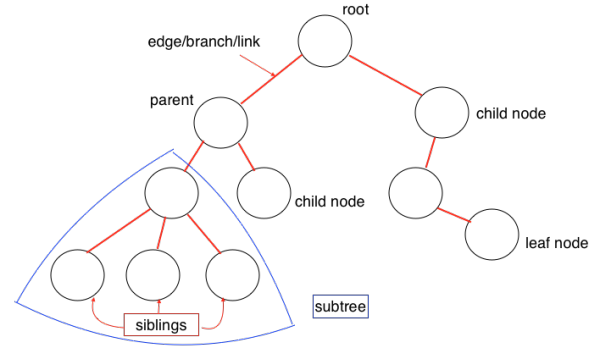
顧名思義，Tree的數據結構和自然界中的樹極其相似，有根、樹枝、葉子，如上圖所示。Tree是一種多層數據結構，與Array、Stack、Queue相比是一種非線性的數據結構，在進行插入和搜索操作時很高效。在描述一個Tree時經常會用到下列概念：

1. Root(根)：代表樹的根節點，根節點沒有父節點

2. Parent Node(父節點)：一個節點的直接上級節點，只有一個

3. Child Node(子節點)：一個節點的直接下級節點，可能有多個

4. Siblings(兄弟節點)：具有相同父節點的節點

5. Leaf(葉節點)：沒有子節點的節點

6. Edge(邊)：兩個節點之間的連接線

7. Path(路徑)：從源節點到目標節點的連續邊

8. Height of Node(節點的高度)：表示節點與葉節點之間的最長路徑上邊的個數

9. Height of Tree(樹的高度)：即根節點的高度

10. Depth of Node(節點的深度)：表示從根節點到該節點的邊的個數

11. Degree of Node(節點的度)：表示子節點的個數

我們以二叉查找樹為例，展示樹在Javascript中的實現。在二叉查找樹中，即每個節點最多只有兩個子節點，而左側子節點小于當前節點，而右側子節點大于當前節點，如圖所示：

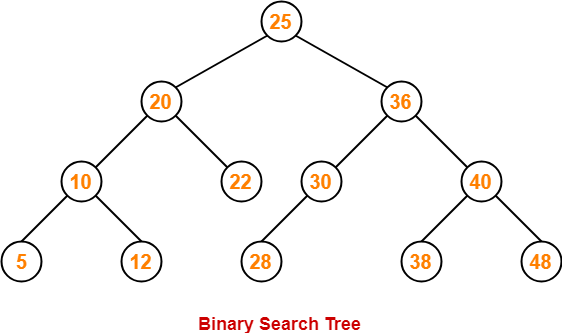
一個二叉查找樹應該具有以下常用方法：

1. add：向樹中插入一個節點

2. findMin：查找樹中最小的節點

3. findMax：查找樹中最大的節點

4. find：查找樹中的某個節點

5. isPresent：判斷某個節點在樹中是否存在

6. remove：移除樹中的某個節點

以下是二叉查找樹的Javascript實現：

class Node {   constructor(data, left = null, right = null) {     this.data = data;     this.left = left;     this.right = right;   } }  class BST {   constructor() {     this.root = null;   }    add(data) {     const node = this.root;     if (node === null) {       this.root = new Node(data);       return;     } else {       const searchTree = function (node) {         if (data < node.data) {           if (node.left === null) {             node.left = new Node(data);             return;           } else if (node.left !== null) {             return searchTree(node.left);           }         } else if (data > node.data) {           if (node.right === null) {             node.right = new Node(data);             return;           } else if (node.right !== null) {             return searchTree(node.right);           }         } else {           return null;         }       };       return searchTree(node);     }   }    findMin() {     let current = this.root;     while (current.left !== null) {       current = current.left;     }     return current.data;   }    findMax() {     let current = this.root;     while (current.right !== null) {       current = current.right;     }     return current.data;   }    find(data) {     let current = this.root;     while (current.data !== data) {       if (data < current.data) {         current = current.left       } else {         current = current.right;       }       if (current === null) {         return null;       }     }     return current;   }    isPresent(data) {     let current = this.root;     while (current) {       if (data === current.data) {         return true;       }       if (data < current.data) {         current = current.left;       } else {         current = current.right;       }     }     return false;   }    remove(data) {     const removeNode = function (node, data) {       if (node == null) {         return null;       }       if (data == node.data) {         // node沒有子節點         if (node.left == null && node.right == null) {           return null;         }         // node沒有左側子節點         if (node.left == null) {           return node.right;         }         // node沒有右側子節點         if (node.right == null) {           return node.left;         }         // node有兩個子節點         var tempNode = node.right;         while (tempNode.left !== null) {           tempNode = tempNode.left;         }         node.data = tempNode.data;         node.right = removeNode(node.right, tempNode.data);         return node;       } else if (data < node.data) {         node.left = removeNode(node.left, data);         return node;       } else {         node.right = removeNode(node.right, data);         return node;       }     }     this.root = removeNode(this.root, data);   } }

測試一下：

const bst = new BST();  bst.add(4); bst.add(2); bst.add(6); bst.add(1); bst.add(3); bst.add(5); bst.add(7); bst.remove(4); console.log(bst.findMin()); console.log(bst.findMax()); bst.remove(7); console.log(bst.findMax()); console.log(bst.isPresent(4));

打印結果：

1 7 6 false

7. Trie(字典樹，讀音同try)

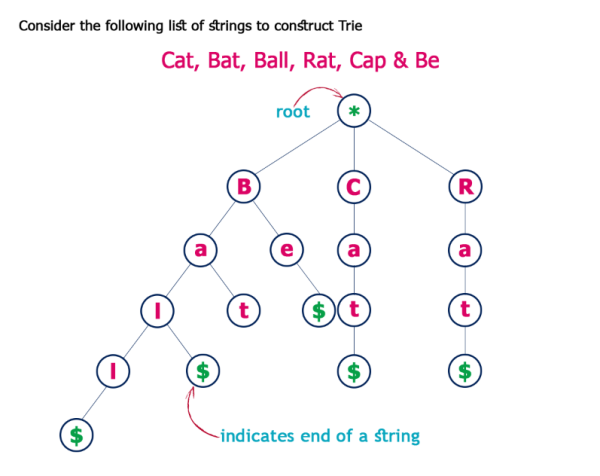
Trie也可以叫做Prefix  Tree(前綴樹)，也是一種搜索樹。Trie分步驟存儲數據，樹中的每個節點代表一個步驟，trie常用于存儲單詞以便快速查找，比如實現單詞的自動完成功能。  Trie中的每個節點都包含一個單詞的字母，跟著樹的分支可以可以拼寫出一個完整的單詞，每個節點還包含一個布爾值表示該節點是否是單詞的最后一個字母。

Trie一般有以下方法：

• add：向字典樹中增加一個單詞

• isWord：判斷字典樹中是否包含某個單詞

• print：返回字典樹中的所有單詞 

/**  * Trie的節點  */ function Node() {   this.keys = new Map();   this.end = false;   this.setEnd = function () {     this.end = true;   };   this.isEnd = function () {     return this.end;   } }  function Trie() {   this.root = new Node();    this.add = function (input, node = this.root) {     if (input.length === 0) {       node.setEnd();       return;     } else if (!node.keys.has(input[0])) {       node.keys.set(input[0], new Node());       return this.add(input.substr(1), node.keys.get(input[0]));     } else {       return this.add(input.substr(1), node.keys.get(input[0]));     }   }    this.isWord = function (word) {     let node = this.root;     while (word.length > 1) {       if (!node.keys.has(word[0])) {         return false;       } else {         node = node.keys.get(word[0]);         word = word.substr(1);       }     }     return (node.keys.has(word) && node.keys.get(word).isEnd()) ? true : false;   }    this.print = function () {     let words = new Array();     let search = function (node = this.root, string) {       if (node.keys.size != 0) {         for (let letter of node.keys.keys()) {           search(node.keys.get(letter), string.concat(letter));         }         if (node.isEnd()) {           words.push(string);         }       } else {         string.length > 0 ? words.push(string) : undefined;         return;       }     };     search(this.root, new String());     return words.length > 0 ? words : null;   } }

8. Graph(圖)

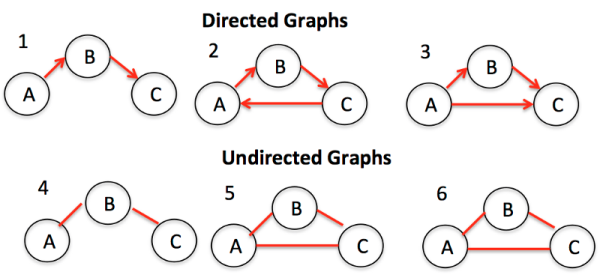
Graph是節點(或頂點)以及它們之間的連接(或邊)的集合。Graph也可以稱為Network(網絡)。根據節點之間的連接是否有方向又可以分為Directed  Graph(有向圖)和Undrected Graph(無向圖)。Graph在實際生活中有很多用途，比如：導航軟件計算最佳路徑，社交軟件進行好友推薦等等。

Graph通常有兩種表達方式：

Adjaceny List(鄰接列表)：

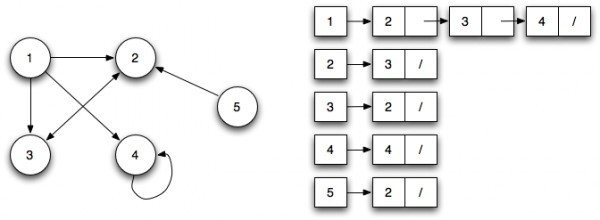
鄰接列表可以表示為左側是節點的列表，右側列出它所連接的所有其他節點。

和 Adjacency Matrix(鄰接矩陣)：

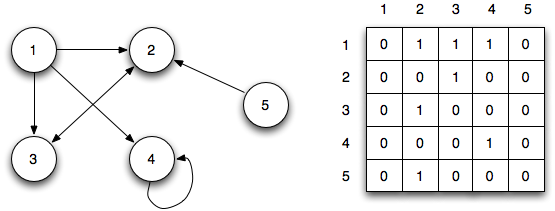
鄰接矩陣用矩陣來表示節點之間的連接關系，每行或者每列表示一個節點，行和列的交叉處的數字表示節點之間的關系：0表示沒用連接，1表示有連接，大于1表示不同的權重。

訪問Graph中的節點需要使用遍歷算法，遍歷算法又分為廣度優先和深度優先，主要用于確定目標節點和根節點之間的距離，

在Javascript中，Graph可以用一個矩陣(二維數組)表示，廣度優先搜索算法可以實現如下：

function bfs(graph, root) {   var nodesLen = {};    for (var i = 0; i < graph.length; i++) {     nodesLen[i] = Infinity;   }    nodesLen[root] = 0;    var queue = [root];   var current;    while (queue.length != 0) {     current = queue.shift();      var curConnected = graph[current];     var neighborIdx = [];     var idx = curConnected.indexOf(1);     while (idx != -1) {       neighborIdx.push(idx);       idx = curConnected.indexOf(1, idx + 1);     }      for (var j = 0; j < neighborIdx.length; j++) {       if (nodesLen[neighborIdx[j]] == Infinity) {         nodesLen[neighborIdx[j]] = nodesLen[current] + 1;         queue.push(neighborIdx[j]);       }     }   }    return nodesLen; }

測試一下：

var graph = [   [0, 1, 1, 1, 0],   [0, 0, 1, 0, 0],   [1, 1, 0, 0, 0],   [0, 0, 0, 1, 0],   [0, 1, 0, 0, 0] ];  console.log(bfs(graph, 1));

打印：

{   0: 2,   1: 0,   2: 1,   3: 3,   4: Infinity }

感謝各位的閱讀，以上就是“Javascript常見數據結構的實現方法是什么”的內容了，經過本文的學習后，相信大家對Javascript常見數據結構的實現方法是什么這一問題有了更深刻的體會，具體使用情況還需要大家實踐驗證。這里是億速云，小編將為大家推送更多相關知識點的文章，歡迎關注！