您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
這篇文章主要介紹“web常用數據結構及復雜度實例分析”,在日常操作中,相信很多人在web常用數據結構及復雜度實例分析問題上存在疑惑,小編查閱了各式資料,整理出簡單好用的操作方法,希望對大家解答”web常用數據結構及復雜度實例分析”的疑惑有所幫助!接下來,請跟著小編一起來學習吧!
如何選擇數據結構
Array (T[])
當元素的數量是固定的,并且需要使用下標時。
Linked list (LinkedList<T>)
當元素需要能夠在列表的兩端添加時。否則使用 List<T>。
Resizable array list (List<T>)
當元素的數量不是固定的,并且需要使用下標時。
Stack (Stack<T>)
當需要實現 LIFO(Last In First Out)時。
Queue (Queue<T>)
當需要實現 FIFO(First In First Out)時。
Hash table (Dictionary<K,T>)
當需要使用鍵值對(Key-Value)來快速添加和查找,并且元素沒有特定的順序時。
Tree-based dictionary (SortedDictionary<K,T>)
當需要使用價值對(Key-Value)來快速添加和查找,并且元素根據 Key 來排序時。
Hash table based set (HashSet<T>)
當需要保存一組唯一的值,并且元素沒有特定順序時。
Tree based set (SortedSet<T>)
當需要保存一組唯一的值,并且元素需要排序時。
Array
在計算機程序設計中,數組(Array)是最簡單的而且應用最廣泛的數據結構之一。在任何編程語言中,數組都有一些共性:
數組中的內容是使用連續的內存(Contiguous Memory)來存儲的。
數組中的所有元素必須是相同的類型,或者類型的衍生類型。因此數組又被認為是同質數據結構(Homegeneous Data Structures)。
數組的元素可以直接被訪問。比如你需要訪問數組的第 i 個元素,則可以直接使用 arrayName[i] 來訪問。
對于數組的常規操作包括:
分配空間(Allocation)
數據訪問(Accessing)
在 C# 中,可以通過如下的方式聲明數組變量。
1 int allocationSize = 10;2 bool[] booleanArray = new bool[allocationSize];3 FileInfo[] fileInfoArray = new FileInfo[allocationSize];
上面的代碼將在 CLR 托管堆中分配一塊連續的內存空間,用以容納數量為 allocationSize ,類型為 arrayType 的數組元素。如果 arrayType 為值類型,則將會有 allocationSize 個未封箱(unboxed)的 arrayType 值被創建。如果 arrayType 為引用類型,則將會有 allocationSize 個 arrayType 類型的引用被創建。

如果我們為 FileInfo[] 數組中的一些位置賦上值,則引用關系為下圖所示。
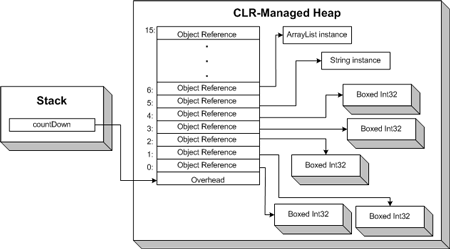
但這些靈活性是以犧牲性能為代價的。在上面 Array 的描述中,我們知道 Array 在存儲值類型時是采用未裝箱(unboxed)的方式。由于 ArrayList 的 Add 方法接受 object 類型的參數,導致如果添加值類型的值會發生裝箱(boxing)操作。這在頻繁讀寫 ArrayList 時會產生額外的開銷,導致性能下降。
List<T>
當 .NET 中引入泛型功能后,上面 ArrayList 所帶來的性能代價可以使用泛型來消除。.NET 提供了新的數組類型 List<T>。
泛型允許開發人員在創建數據結構時推遲數據類型的選擇,直到使用時才確定選擇哪種類型。泛型(Generics)的主要優點包括:
類型安全(Type Safety):使用泛型定義的類型,在使用時僅能使用指定的類型或類型的衍生類型。
性能(Performance):泛型移除了運行時類型檢測,消除了裝箱和拆箱的開銷。
可重用(Reusability):泛型打破了數據結構與存儲數據類型之間的緊耦合。這提高了數據結構的可重用性。
List<T> 等同于同質的一維數組(Homogeneous self-redimensioning array)。它像 Array 一樣可以快速的讀取元素,還可以保持長度可變的靈活性。
1 // 創建 int 類型列表2 List<int> myFavoriteIntegers = new List<int>();3 4 // 創建 string 類型列表5 List<string> friendsNames = new List<string>();
List<T> 內部同樣使用 Array 來實現,但它隱藏了這些實現的復雜性。當創建 List<T> 時無需指定初始長度,當添加元素到 List<T> 中時,也無需關心數組大小的調整(resize)問題。
1 List<int> powersOf2 = new List<int>();2 3 powersOf2.Add(1);4 powersOf2.Add(2);5 6 powersOf2[1] = 10;7 8 int sum = powersOf2[1] + powersOf2[2];
List<T> 的漸進運行時(Asymptotic Running Time)復雜度與 Array 是相同的。
Queue<T>
當我們需要使用先進先出順序(FIFO)的數據結構時,.NET 為我們提供了 Queue<T>。Queue<T> 類提供了 Enqueue 和 Dequeue 方法來實現對 Queue<T> 的存取。
Queue<T> 內部建立了一個存放 T 對象的環形數組,并通過 head 和 tail 變量來指向該數組的頭和尾。
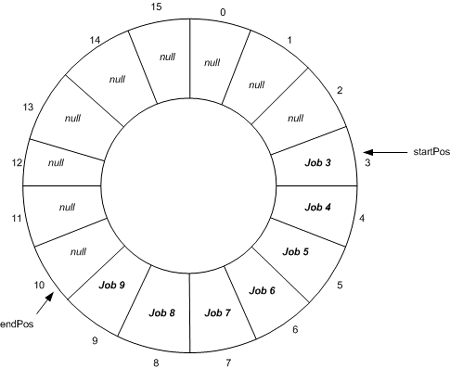
默認情況下,Queue<T> 的初始化容量是 32,也可以通過構造函數指定容量。
Enqueue 方法會判斷 Queue<T> 中是否有足夠容量存放新元素。如果有,則直接添加元素,并使索引 tail 遞增。在這里的 tail 使用求模操作以保證 tail 不會超過數組長度。如果容量不夠,則 Queue<T> 根據特定的增長因子擴充數組容量。
默認情況下,增長因子(growth factor)的值為 2.0,所以內部數組的長度會增加一倍。也可以通過構造函數中指定增長因子。Queue<T> 的容量也可以通過 TrimExcess 方法來減少。
Dequeue 方法根據 head 索引返回當前元素,之后將 head 索引指向 null,再遞增 head 的值。
Stack<T>
當需要使用后進先出順序(LIFO)的數據結構時,.NET 為我們提供了 Stack<T>。Stack<T> 類提供了 Push 和 Pop 方法來實現對 Stack<T> 的存取。
Stack<T> 中存儲的元素可以通過一個垂直的集合來形象的表示。當新的元素壓入棧中(Push)時,新元素被放到所有其他元素的頂端。當需要彈出棧(Pop)時,元素則被從頂端移除。
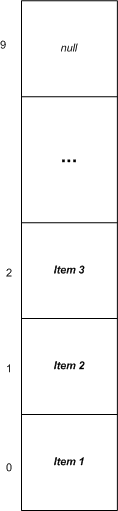
Stack<T> 的默認容量是 10。和 Queue<T> 類似,Stack<T> 的初始容量也可以在構造函數中指定。Stack<T> 的容量可以根據實際的使用自動的擴展,并且可以通過 TrimExcess 方法來減少容量。
如果 Stack<T> 中元素的數量 Count 小于其容量,則 Push 操作的復雜度為 O(1)。如果容量需要被擴展,則 Push 操作的復雜度變為 O(n)。Pop 操作的復雜度始終為 O(1)。
Hashtable
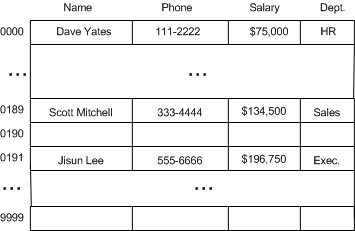
現在我們要使用員工的社保號作為唯一標識進行存儲。社保號的格式為 DDD-DD-DDDD(D 的范圍為數字 0-9)。
如果使用 Array 存儲員工信息,要查詢社保號為 111-22-3333 的員工,則將會嘗試遍歷數組的所有選擇,即執行復雜度為 O(n) 的查詢操作。好一些的辦法是將社保號排序,以使查詢復雜度降低到 O(log(n))。但理想情況下,我們更希望查詢復雜度為 O(1)。
一種方案是建立一個大數組,范圍從 000-00-0000 到 999-99-9999 。
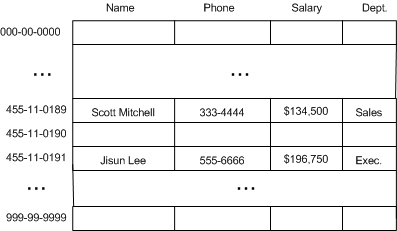
這種方案的缺點是浪費空間。如果我們僅需要存儲 1000 個員工的信息,那么僅利用了 0.0001% 的空間。
第二種方案就是用哈希函數(Hash Function)壓縮序列。
我們選擇使用社保號的后四位作為索引,以減少區間的跨度。這樣范圍將從 0000 到 9999。
在數學上,將這種從 9 位數轉換為 4 位數的方式稱為哈希轉換(Hashing)。可以將一個數組的索引空間(indexers space)壓縮至相應的哈希表(Hash Table)。
在上面的例子中,哈希函數的輸入為 9 位數的社保號,輸出結果為后 4 位。
H(x) = last four digits of x
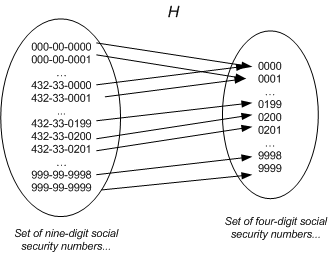
上圖中也說明在哈希函數計算中常見的一種行為:哈希沖突(Hash Collisions)。即有可能兩個社保號的后 4 位均為 0000。
當要添加新元素到 Hashtable 中時,哈希沖突是導致操作被破壞的一個因素。如果沒有沖突發生,則元素被成功插入。如果發生了沖突,則需要判斷沖突的原因。因此,哈希沖突提高了操作的代價,Hashtable 的設計目標就是要盡可能減低沖突的發生。
避免哈希沖突的一個方法就是選擇合適的哈希函數。哈希函數中的沖突發生的幾率與數據的分布有關。例如,如果社保號的后 4 位是隨即分布的,則使用后 4 位數字比較合適。但如果后 4 位是以員工的出生年份來分配的,則顯然出生年份不是均勻分布的,則選擇后 4 位會造成大量的沖突。
我們將選擇合適的哈希函數的方法稱為沖突避免機制(Collision Avoidance)。
在處理沖突時,有很多策略可以實施,這些策略稱為沖突解決機制(Collision Resolution)。其中一種方法就是將要插入的元素放到另外一個塊空間中,因為相同的哈希位置已經被占用。
例如,最簡單的一種實現就是線性挖掘(Linear Probing),步驟如下:
當插入新的元素時,使用哈希函數在哈希表中定位元素位置;
檢查哈希表中該位置是否已經存在元素。如果該位置內容為空,則插入并返回,否則轉向步驟 3。
如果該位置為 i,則檢查 i+1 是否為空,如果已被占用,則檢查 i+2,依此類推,直到找到一個內容為空的位置。
現在如果我們要將五個員工的信息插入到哈希表中:
Alice (333-33-1234)
Bob (444-44-1234)
Cal (555-55-1237)
Danny (000-00-1235)
Edward (111-00-1235)
則插入后的哈希表可能如下:
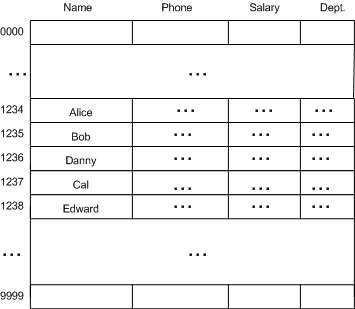
元素的插入過程:
Alice 的社保號被哈希為 1234,因此存放在位置 1234。
Bob 的社保號被哈希為 1234,但由于位置 1234 處已經存放 Alice 的信息,則檢查下一個位置 1235,1235 為空,則 Bob 的信息就被放到 1235。
Cal 的社保號被哈希為 1237,1237 位置為空,所以 Cal 就放到 1237 處。
Danny 的社保號被哈希為 1235,1235 已被占用,則檢查 1236 位置是否為空,1236 為空,所以 Danny 就被放到 1236。
Edward 的社保號被哈希為 1235,1235 已被占用,檢查1236,也被占用,再檢查1237,直到檢查到 1238時,該位置為空,于是 Edward 被放到了1238 位置。
線性挖掘(Linear Probing)方式雖然簡單,但并不是解決沖突的最好的策略,因為它會導致同類哈希的聚集。這導致搜索哈希表時,沖突依然存在。例如上面例子中的哈希表,如果我們要訪問 Edward 的信息,因為 Edward 的社保號 111-00-1235 哈希為 1235,然而我們在 1235 位置找到的是 Bob,所以再搜索 1236,找到的卻是 Danny,以此類推直到找到 Edward。
一種改進的方式為二次挖掘(Quadratic Probing),即每次檢查位置空間的步長為平方倍數。也就是說,如果位置 s 被占用,則首先檢查 s + 12 處,然后檢查s - 12,s + 22,s - 22,s + 32 依此類推,而不是象線性挖掘那樣以 s + 1,s + 2 ... 方式增長。盡管如此,二次挖掘同樣也會導致同類哈希聚集問題。
.NET 中的 Hashtable 的實現,要求添加元素時不僅要提供元素(Item),還要為該元素提供一個鍵(Key)。例如,Key 為員工社保號,Item 為員工信息對象。可以通過 Key 作為索引來查找 Item。
1 Hashtable employees = new Hashtable(); 2 3 // Add some values to the Hashtable, indexed by a string key 4 employees.Add("111-22-3333", "Scott"); 5 employees.Add("222-33-4444", "Sam"); 6 employees.Add("333-44-55555", "Jisun"); 7 8 // Access a particular key 9 if (employees.ContainsKey("111-22-3333"))10 {11 string empName = (string)employees["111-22-3333"];12 Console.WriteLine("Employee 111-22-3333's name is: " + empName);13 }14 else15 Console.WriteLine("Employee 111-22-3333 is not in the hash table...");Hashtable 類中的哈希函數比前面介紹的社保號的實現要更為復雜。哈希函數必須返回一個序數(Ordinal Value)。對于社保號的例子,通過截取后四位就可以實現。但實際上 Hashtable 類可以接受任意類型的值作為 Key,這都要歸功于 GetHashCode 方法,一個定義在 System.Object 中的方法。GetHashCode 的默認實現將返回一個唯一的整數,并且保證在對象的生命周期內保持不變。
Hashtable 類中的哈希函數定義如下:
H(key) = [GetHash(key) + 1 + (((GetHash(key) >> 5) + 1) % (hashsize – 1))] % hashsize
這里的 GetHash(key) 默認是調用 key 的 GetHashCode 方法以獲取返回的哈希值。hashsize 指的是哈希表的長度。因為要進行求模,所以最后的結果 H(key) 的范圍在 0 至 hashsize - 1 之間。
當在哈希表中添加或獲取一個元素時,會發生哈希沖突。前面我們簡單地介紹了兩種沖突解決策略:
線性挖掘(Linear Probing)
二次挖掘(Quadratic Probing)
在 Hashtable 類中則使用的是一種完全不同的技術,稱為二度哈希(rehashing)(有些資料中也將其稱為雙精度哈希(double hashing))。
二度哈希的工作原理如下:
有一個包含一組哈希函數 H1...Hn 的集合。當需要從哈希表中添加或獲取元素時,首先使用哈希函數 H1。如果導致沖突,則嘗試使用 H2,以此類推,直到 Hn。所有的哈希函數都與 H1 十分相似,不同的是它們選用的乘法因子(multiplicative factor)。
通常,哈希函數 Hk 的定義如下:
Hk(key) = [GetHash(key) + k * (1 + (((GetHash(key) >> 5) + 1) % (hashsize – 1)))] % hashsize
當使用二度哈希時,重要的是在執行了 hashsize 次挖掘后,哈希表中的每一個位置都有且只有一次被訪問到。也就是說,對于給定的 key,對哈希表中的同一位置不會同時使用 Hi 和 Hj。在 Hashtable 類中使用二度哈希公式,其始終保持 (1 + (((GetHash(key) >> 5) + 1) % (hashsize – 1)) 與 hashsize 互為素數(兩數互為素數表示兩者沒有共同的質因子)。
二度哈希較前面介紹的線性挖掘(Linear Probing)和二次挖掘(Quadratic Probing)提供了更好的避免沖突的策略。
Hashtable 類中包含一個私有成員變量 loadFactor,loadFactor 指定了哈希表中元素數量與位置(slot)數量之間的最大比例。例如:如果 loadFactor 等于 0.5,則說明哈希表中只有一半的空間存放了元素值,其余一半都為空。
哈希表的構造函數允許用戶指定 loadFactor 值,定義范圍為 0.1 到 1.0。然而,不管你提供的值是多少,范圍都不會超過 72%。即使你傳遞的值為 1.0,Hashtable 類的 loadFactor 值還是 0.72。微軟認為loadFactor 的最佳值為 0.72,這平衡了速度與空間。因此雖然默認的 loadFactor 為 1.0,但系統內部卻自動地將其改變為 0.72。所以,建議你使用缺省值1.0(但實際上是 0.72)。
向 Hashtable 中添加新元素時,需要檢查以保證元素與空間大小的比例不會超過最大比例。如果超過了,哈希表空間將被擴充。步驟如下:
哈希表的位置空間幾乎被翻倍。準確地說,位置空間值從當前的素數值增加到下一個最大的素數值。
因為二度哈希時,哈希表中的所有元素值將依賴于哈希表的位置空間值,所以表中所有值也需要重新二度哈希。
由此看出,對哈希表的擴充將是以性能損耗為代價。因此,我們應該預先估計哈希表中最有可能容納的元素數量,在初始化哈希表時給予合適的值進行構造,以避免不必要的擴充。
Dictionary<K,T>
Hashtable 類是一個類型松耦合的數據結構,開發人員可以指定任意的類型作為 Key 或 Item。當 .NET 引入泛型支持后,類型安全的 Dictionary<K,T> 類出現。Dictionary<K,T> 使用強類型來限制 Key 和 Item,當創建 Dictionary<K,T> 實例時,必須指定 Key 和 Item 的類型。
Dictionary<keyType, valueType> variableName = new Dictionary<keyType, valueType>();
如果繼續使用上面描述的社保號和員工的示例,我們可以創建一個 Dictionary<K,T> 的實例:
Dictionary<int, Employee> employeeData = new Dictionary<int, Employee>();
這樣我們就可以添加和刪除員工信息了。
1 // Add some employees2 employeeData.Add(455110189) = new Employee("Scott Mitchell");3 employeeData.Add(455110191) = new Employee("Jisun Lee");4 5 // See if employee with SSN 123-45-6789 works here6 if (employeeData.ContainsKey(123456789))Dictionary<K,T> 與 Hashtable 的不同之處還不止一處。除了支持強類型外,Dictionary<K,T> 還采用了不同的沖突解決策略(Collision Resolution Strategy),這種新的技術稱為鏈技術(chaining)。
前面使用的挖掘技術(probing),如果發生沖突,則將嘗試列表中的下一個位置。如果使用二度哈希(rehashing),則將導致所有的哈希被重新計算。而新的鏈技術(chaining)將采用額外的數據結構來處理沖突。Dictionary<K,T> 中的每個位置(slot)都映射到了一個數組。當沖突發生時,沖突的元素將被添加到桶(bucket)列表中。
下面的示意圖中描述了 Dictionary<K,T> 中的每個桶(bucket)都包含了一個鏈表以存儲相同哈希的元素。
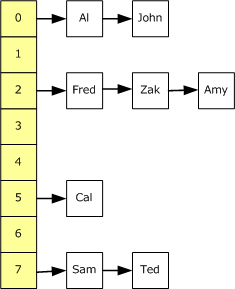
上圖中,該 Dictionary 包含了 8 個桶,也就是自頂向下的黃色背景的位置。一定數量的 Employee 對象已經被添加至 Dictionary 中。如果一個新的 Employee 要被添加至 Dictionary 中,將會被添加至其 Key 的哈希所對應的桶中。如果在相同位置已經有一個 Employee 存在了,則將會將新元素添加到列表的前面。
向 Dictionary 中添加元素的操作涉及到哈希計算和鏈表操作,但其仍為常量,復雜度為 O(1)。
對 Dictionary 進行查詢和刪除操作時,其平均時間取決于 Dictionary 中元素的數量和桶(bucket)的數量。具體的說就是運行時間為 O(n/m),這里 n 為元素的總數量,m 是桶的數量。但 Dictionary 幾乎總是被實現為 n = m,也就是說,元素的總數絕不會超過桶的總數。所以 O(n/m) 也變成了常量 O(1)。
到此,關于“web常用數據結構及復雜度實例分析”的學習就結束了,希望能夠解決大家的疑惑。理論與實踐的搭配能更好的幫助大家學習,快去試試吧!若想繼續學習更多相關知識,請繼續關注億速云網站,小編會繼續努力為大家帶來更多實用的文章!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。