您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
本篇內容主要講解“如何通過代碼實現二叉搜索樹”,感興趣的朋友不妨來看看。本文介紹的方法操作簡單快捷,實用性強。下面就讓小編來帶大家學習“如何通過代碼實現二叉搜索樹”吧!
首先,二叉搜索樹到底是什么?
二叉搜索樹(BST)是一種特殊類型的樹形數據結構,由節點及其子節點組成,子節點也被視作“后代”,可以把它想象成一棵倒置的樹或者是樹的根部。
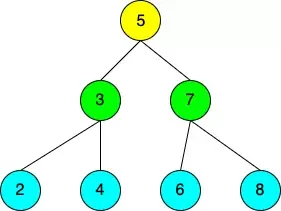
每個節點最多只能有2個子節點:左節點和右節點。為了使它成為一個有效的二叉搜索樹,左節點的值必須總是小于母節點,而右節點的值必須總是大于母節點。沒有任何間隙的BST,即每個節點都有一個左節點和一個右節點的二叉搜索樹,被稱為“完美”樹。
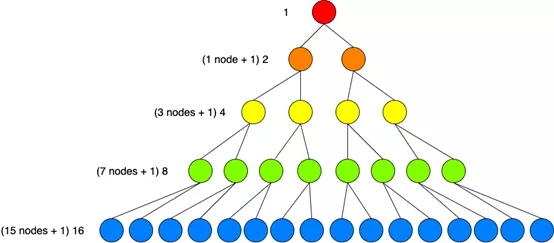
在完美樹中,當遍歷樹時,每個級別中的節點數會翻倍,將前面的所有節點相加并在該數字上再添加“1”可以得出底層的節點總數。
當在平衡二叉搜索樹中搜索一個元素時,平均需要花費額的時間為O(log n),在最壞的情況下,需要O(n)。你可以把在二叉搜索樹中的搜索看作是“選擇你自己的冒險”模型,從頂部節點開始,然后沿著樹向下,在到達的每個節點問同樣的2個問題。
我要找的值是否小于當前節點?如果是,向左走。
我要找的值是否大于當前節點?如果是,向右走。
插入和刪除也非常快,平均花費O(log n)的時間。但有一個缺點就是不能像數組那樣獲得隨機元素。
什么時候可以使用二叉搜索樹?
假設你需要為Facebook這樣的社交媒體應用程序設計一個數據庫。該數據庫需要處理數百萬個用戶名,并且需要在登錄期間快速檢索到其中一個用戶名。由于每天都有新注冊或刪除的賬戶,你也需要方便進行插入和刪除的操作。
通過一個排序過的數組進行二分搜索會非常快(需要花費O(log n)時間),但是插入或刪除一個用戶名會導致整個數組重新排序,需要花費O(n)時間,這取決于數組的大小,可能會相對慢一些。如果我們使用二叉搜索樹,插入或刪除的時間會快得多(花費O(log n)時間)。
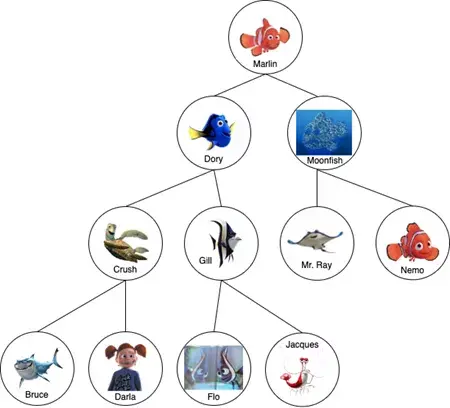
如果有一個帶有名字的二叉搜索樹(比如這個《海底總動員》的樹),就可以按字母順序排列。
在字母表中,Dory在Marlin之前,所以它是左邊的節點,而Moonfish在Marlin之后,所以它是右邊的節點。同樣地,在下一層搜索也遵循這個規律。Bruce在Crush之前,也在Dory和Marlin之前。Darla在Crush之后,但在Dory和Marlin之前。
現在準備好,是時候尋找Nemo了!
尋找Nemo!
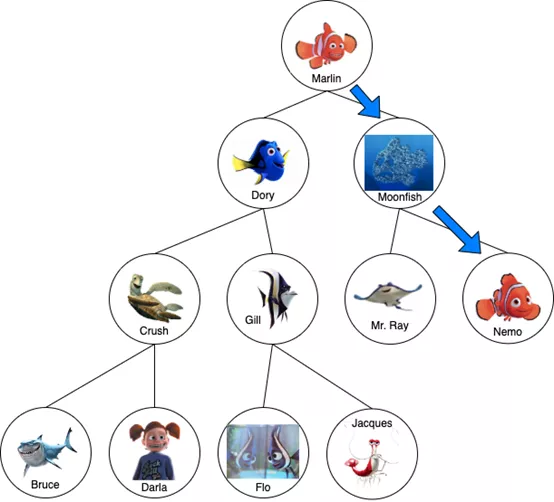
假設已經有一個有效的二叉搜索樹,并且需要找到Nemo。因為我們知道樹中的節點是按字母順序排序的,所以這應該相當簡單。
從Marlin開始,左邊是Dory,右邊是Moonfish。我們知道Nemo在字母表中位于Marlin之后,所以我們將遍歷到正確的節點(Moonfish)。Nemo按字母順序是排在Moonfish之后的,所以繼續往下看Moonfish的右子節點。很幸運,那是…Nemo!找到Nemo了!
效率很高。二叉搜索樹減少了整個搜索過程的時間復雜性!如果樹沒有分類,只是一個普通的樹形結構呢?或者要證實這是個二叉搜索樹呢?目前有兩種不同的搜索技術可以實現這一點。
什么是廣度優先搜索?
廣度優先搜索是一種在樹(或圖形)中一次遍歷一級的方法,每次都從左到右在節點之間移動。
在《海底總動員》的例子中,Marlin首先會問Dory,“你知道我兒子Nemo在哪里嗎?”如果它說不,Marlin就會問Moonfish同樣的問題。如果它也說不,Marlin會再下一層,問Crush、Gill和Mr. Ray,然后Marlin就找到Nemo了!
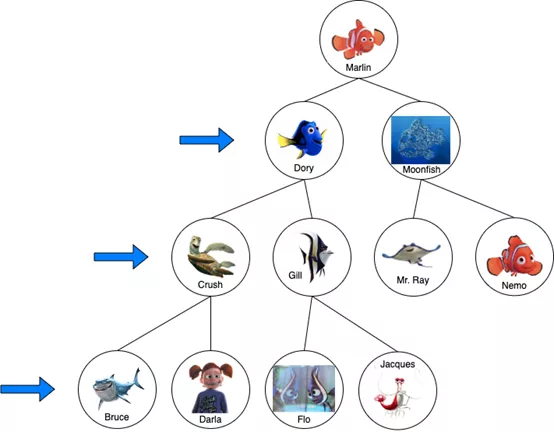
廣度優先搜索
如果在Mr. Ray之后沒有找到Nemo,Marlin會到下一級詢問Bruce和Darla等等。使用廣度優先搜索可以找到起始節點(Marlin)和目標節點(Nemo)之間的最短距離。時間復雜度是O(n),因為在最壞的情況下,需要檢查每個節點才能找到Nemo。
什么是深度優先搜索?
深度優先搜索(Depth first search)是一種從頂部節點一直向下遍歷到其最遠子節點的樹(或圖形)的方法,然后在未找到目標節點時再回去并嘗試其他路徑。
在《海底總動員》的例子中,Marlin首先會問Dory “你知道Nemo在哪里嗎?” 如果她不知道,他就會問Crush同樣的問題,因為Crush是Dory最左邊的子節點。如果Crush也說沒有,Marlin將移動到下一級去問Bruce,盡管他害怕成為鯊魚的點心,但也會問問他有沒有見到自己的兒子。
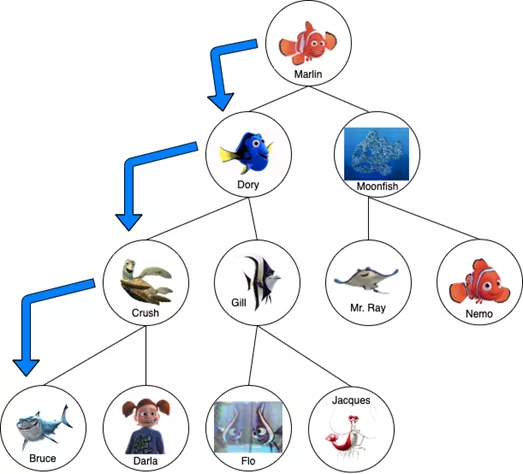
深度優先搜索
如果Bruce說沒看到Nemo,并向Marlin保證“魚是朋友,不是食物”,Marlin就需要回到上級,尋找另一個他還沒有問到的節點。回到Crush那里,他會發現下一步應該問Darla。由于Crush的所有后代現在都被審問過了,Marlin會回到Dory那里,檢查她其余的“后代”。Marlin需要把每個角色詢問一遍后才能找到Nemo。
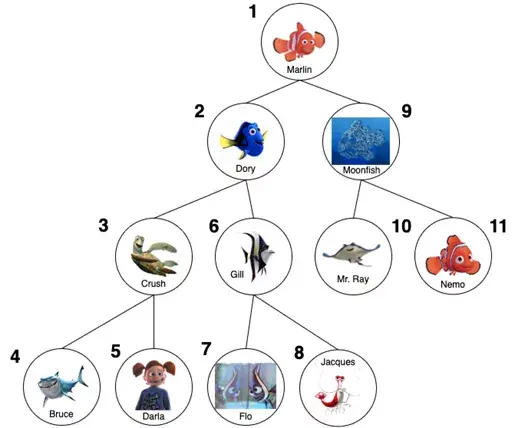
深度優先搜索順序
與廣度優先搜索一樣,深度優先搜索也包括時間復雜度O(n),但空間復雜度可能有所不同。深度優先搜索通常占用較少的內存或空間,假設可以在遍歷整個樹之前找到目標節點。
由于二叉搜索樹中的每增加一級節點會加倍(至少對于平衡樹而言),如果丟失的節點(Nemo)位于樹的較低位置,則可以使用深度優先搜索來節省內存。在最壞的情況下,兩種方法的空間復雜度都是O(n)。
關于二叉搜索樹以及如何通過代碼實現它們還有很多需要學習,但這個有趣的案例會成為你了解數據結構的起點。
到此,相信大家對“如何通過代碼實現二叉搜索樹”有了更深的了解,不妨來實際操作一番吧!這里是億速云網站,更多相關內容可以進入相關頻道進行查詢,關注我們,繼續學習!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。