您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
本篇內容主要講解“何為二叉搜索樹”,感興趣的朋友不妨來看看。本文介紹的方法操作簡單快捷,實用性強。下面就讓小編來帶大家學習“何為二叉搜索樹”吧!
樹是一種數據結構,它是由n(n>=1)個有限結點組成一個具有層次關系的集合。把它叫做“樹”是因為它看起來像一棵倒掛的樹,也就是說它是根朝上,而葉朝下的。
樹是遞歸的,將樹的任何一個節點以及節點下的節點都能組合成一個新的樹,所以樹的很多問題都是使用遞歸去完成。
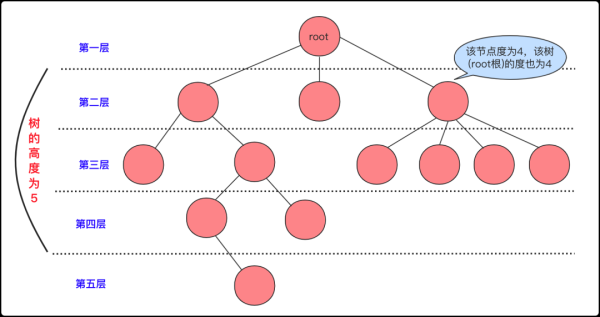
根節點: 最上面的那個節點(root),根節點沒有父節點,只有子節點(0個或多個都可以)
層數: 一般認為根節點是第1層(有的也說第0層),而樹的高度就是層數最高(上圖層數開始為1)節點的層數
節點關系:
父節點:連接該節點的上一層節點,
孩子節點: 和父節點對應,上下關系。而祖先節點是父節點的父節點(或者祖先)節點。
兄弟節點:擁有同一個父節點的節點們!
節點的度: 就是節點擁有孩子節點的個數(是直接連接的孩子不是子孫).
樹的度: 就是所有節點中最大 (節點的度)。同時,如果度大于0的節點是分支節點,度等于0的節點是葉子節點(沒有子孫)。
相關性質:

二叉樹是一樹的一種,但應用比較多,所以需要深入學習,二叉樹的每個節點最多只有兩個子節點(但不一定非得要有兩個節點)。
二叉樹與度為2的樹的區別:
1、度為2的的樹必須有三個節點以上(否則就不叫度為二了,一定要先存在),二叉樹可以為空。
2、二叉樹的度不一定為2,比如斜樹。
3、二叉樹有左右節點區分,而度為2的樹沒有左右節點的區分。
幾種特殊二叉樹:
滿二叉樹:高度為n的滿二叉樹有(2^n) -1個節點
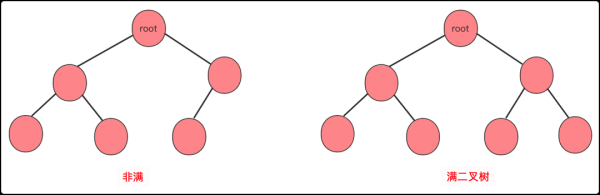
滿二叉樹
完全二叉樹:上面一層全部滿,最下一層從左到右順序排列
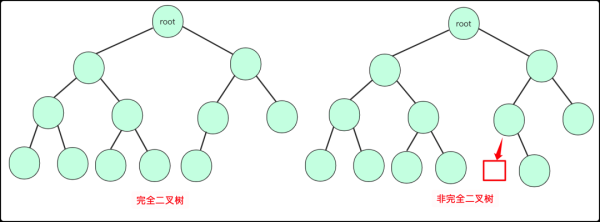
完全二叉樹
二叉排序樹:樹按照一定規則插入排序(本文詳解)。
平衡二叉樹:樹上任意節點左子樹和右子樹深度差距不超過1(后文詳解).
二叉樹性質:
1、二叉樹有用樹的性質
2、非空二叉樹葉子節點數=度為2的節點數+1.本來一個節點如果度為1.那么一直延續就一個葉子,但如果出現一個度為2除了延續原來的一個節點,會多出一個節點需要維系。所以到最后會多出一個葉子。
3、非空第i層最多有2^(i-1)個節點。
4、高為h的樹最多有(2^h)-1個節點(等比求和)。
二叉樹一般用鏈式存儲,這樣內存利用更高,但二叉樹也可以用數組存儲的(經常會遇到),各個節點對應的下標是可以計算出來的,就拿一個完全二叉樹若從左往右,從上到下編號如圖:
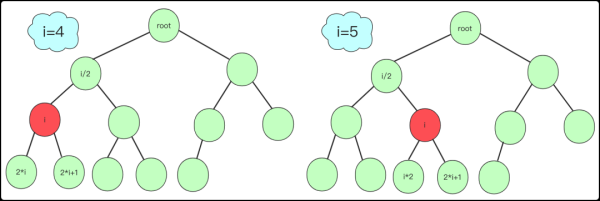
二叉樹節點位置對應關系
前面鋪墊那么多,咱們言歸正傳,詳細講解并實現一個二叉排序樹,二叉搜索樹擁有二叉樹的性質,同時有一些自己的規則:
首先要了解二叉排序樹的規則:從任意節點開始,節點左側節點值總比節點右側值要小。
例如一個二叉排序樹依次插入15,6,23,7,4,71,5,50會形成下圖順序
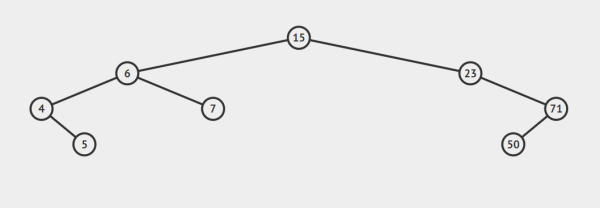
一個二叉排序樹
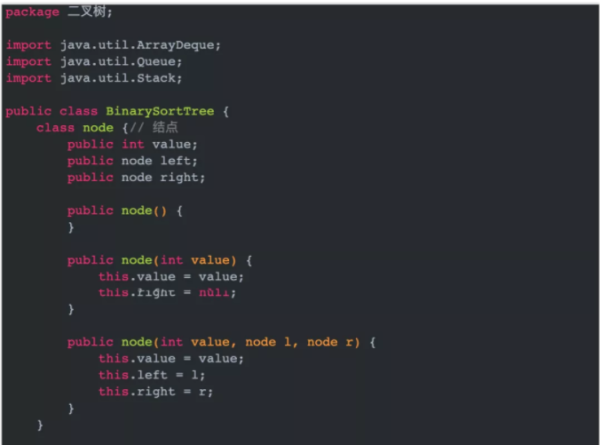
二叉排序樹是由若干節點(node)構成的,對于node需要這些屬性:left,right,和value。其中left和right是左右指針指向左右孩子子樹,而value是儲存的數據,這里用int 類型。
node類構造為:
class node {//結點 public int value; public node left; public node right; public node() { } public node(int value) { this.value=value; this.left=null; this.right=null; } public node(int value,node l,node r) { this.value=value; this.left=l; this.right=r; } }既然節點構造好了,那么就需要節點等其他信息構造成樹,有了鏈表構造經驗,很容易得知一棵樹最主要的還是root根節點。
所以樹的構造為:
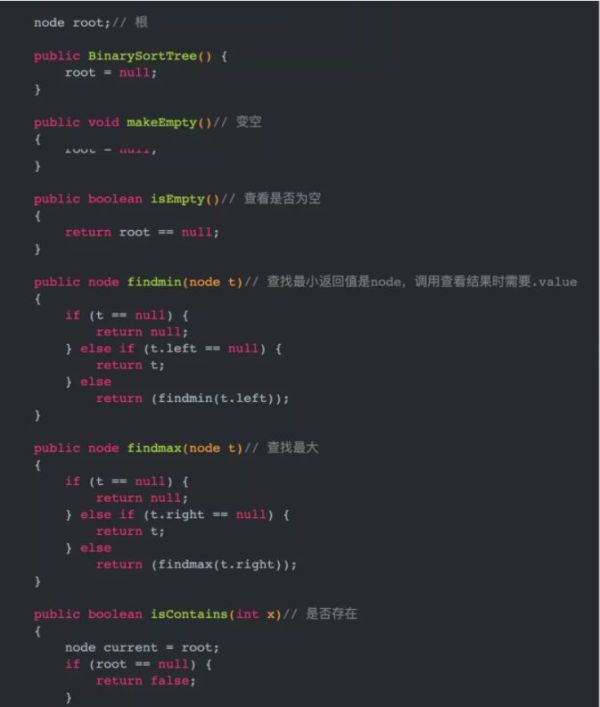
public class BinarySortTree { node root;//根 public BinarySortTree() {root=null;} public void makeEmpty()//變空 {root=null;} public boolean isEmpty()//查看是否為空 {return root==null;} //各種方法 }可以用圖來表示一下這個結構:
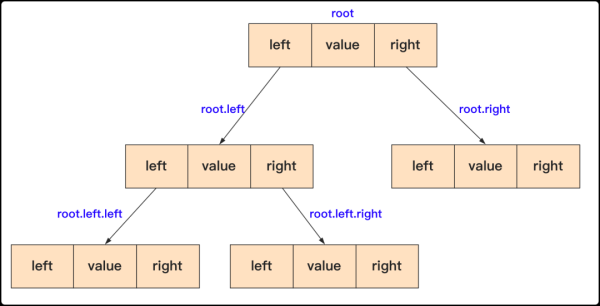
既然已經構造好一棵樹,那么就需要實現主要的方法,因為二叉排序樹中每個節點都能看作一棵樹。所以我們創建方法的是時候加上節點參數(方便一些遞歸調用)
findmin()找到最小節點:
因為所有節點的最小都是往左插入,所以只需要找到最左側的返回即可,具體實現可使用遞歸也可非遞歸while循環。
findmax()找到最大節點:
因為所有節點大的都是往右面插入,所以只需要找到最右側的返回即可,實現方法與findmin()方法一致。
代碼使用遞歸函數
public node findmin(node t)//查找最小返回值是node,調用查看結果時需要.value { if(t==null) {return null;} else if(t.left==null) {return t;} else return(findmin(t.left)); } public node findmax(node t)//查找最大 { if(t==null) {return null;} else if(t.right==null) {return t;} else return(findmax(t.right)); }一個圖中查找最大最小過程如下:
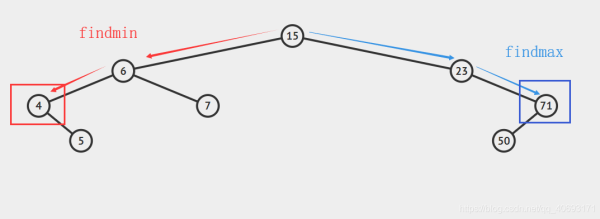
查找過程
這里的意思是查找二叉查找樹中是否存在值為x的節點。
在具體實現上,根據二叉排序樹左側更小,右側更大的性質進行往下查找,如果找到值為x的節點則返回true,如果找不到就返回false,當然實現上可以采用遞歸或者非遞歸,我這里使用非遞歸的方式。
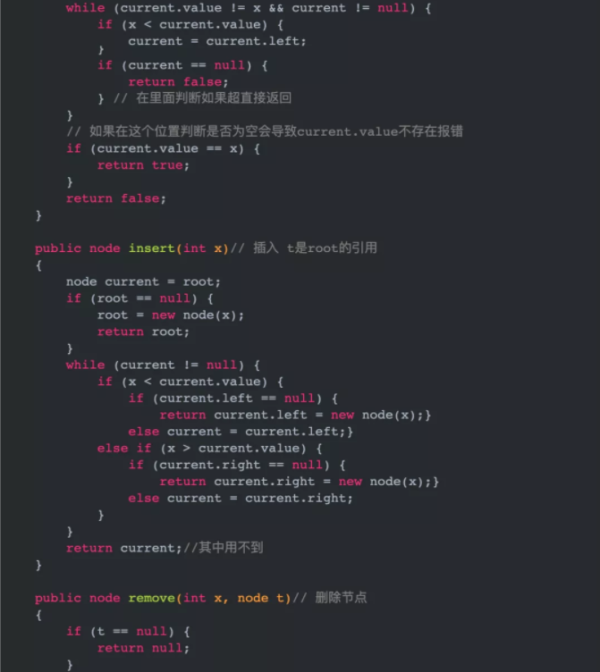
public boolean isContains(int x)//是否存在 { node current=root; if(root==null) {return false;} while(current.value!=x&¤t!=null) { if(x<current.value) {current=current.left;} if(x>current.value) {current=current.right;} if(current==null) {return false;}//在里面判斷如果超直接返回 } //如果在這個位置判斷是否為空會導致current.value不存在報錯 if(current.value==x) {return true;} return false; }插入的思想和前面isContains(int x)類似,找到自己的位置(空位置)插入。
但是具體實現上有需要注意的地方,我們要到待插入位置上一層節點,你可能會疑問為什么不直接找到最后一個空,然后將current賦值過去current=new node(x),這樣的化current就相當于指向一個new node(x)節點,和原來樹就脫離關系(原樹相當于沒有任何操作),所以要提前通過父節點判定是否為空找到位置,找到合適位置通過父節點的left或者right節點指向新創建的節點才能完成插入的操作。
public node insert(int x)// 插入 t是root的引用 { node current = root; if (root == null) { root = new node(x); return root; } while (current != null) { if (x < current.value) { if (current.left == null) { return current.left = new node(x);} else current = current.left;} else if (x > current.value) { if (current.right == null) { return current.right = new node(x);} else current = current.right; } } return current;//其中用不到 }比如說上面樹插入值為51的節點。
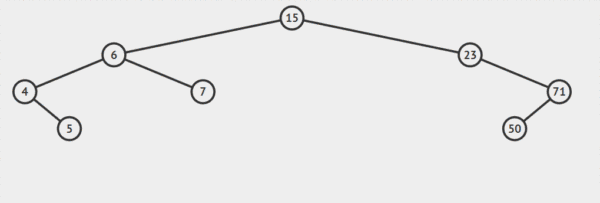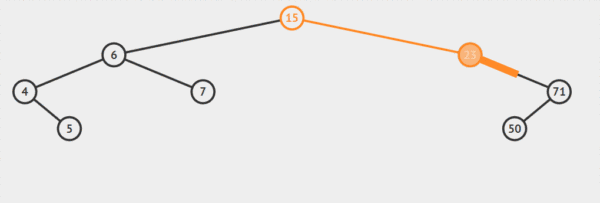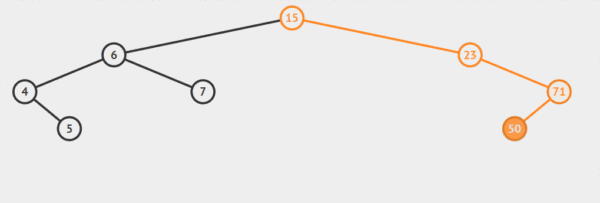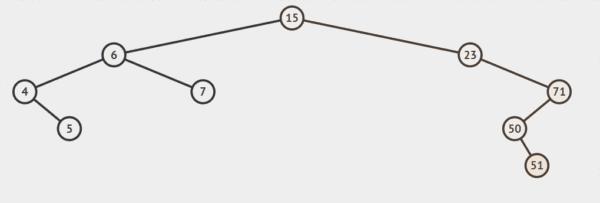
插入值為51的節點
刪除操作算是一個相對較難理解的操作了,因為待刪除的點可能在不同位置所以具體處理的方式也不同,如果是葉子即可可直接刪除,有一個孩子節點用子節點替換即可,有兩個子節點的就要先找到值距離待刪除節點最近的點(左子樹最大點或者右子樹最小點),將值替換掉然后遞歸操作在子樹中刪除已經替換的節點,當然沒具體分析可以看下面:
刪除的節點沒有子孫:
這種情況不需要考慮,直接刪除即可(節點=null即可)(圖中紅色點均滿足這種方式)。
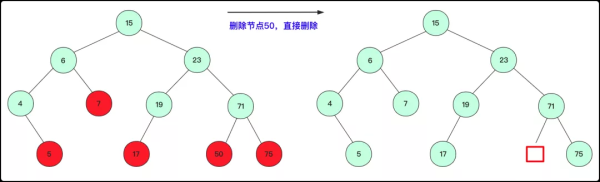
待刪除節點為葉子節點
一個子節點為空:
此種情況也很容易,直接將刪除點的子節點放到被刪除位置即可。
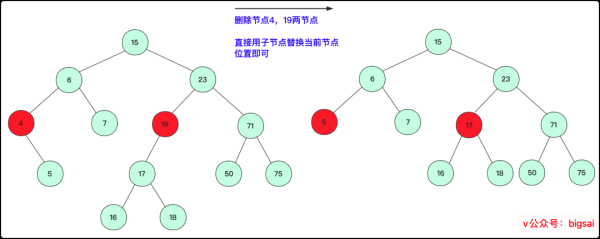
待刪除節點有1個孩子
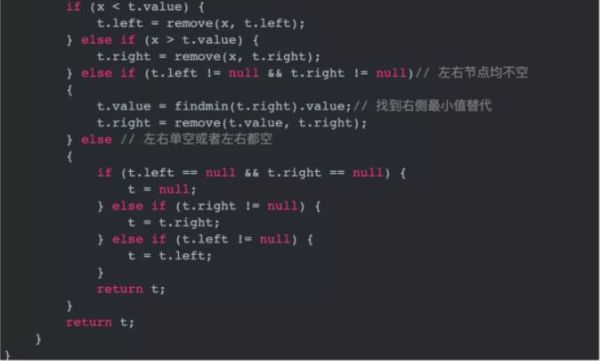
左右節點均不空
左右孩子節點都不為空這種情況是相對比較復雜的,因為不能直接用其中一個孩子節點替代當前節點(放不下,如果孩子節點也有兩個孩子那么有一個節點無法放,例如拿下面71節點替代)
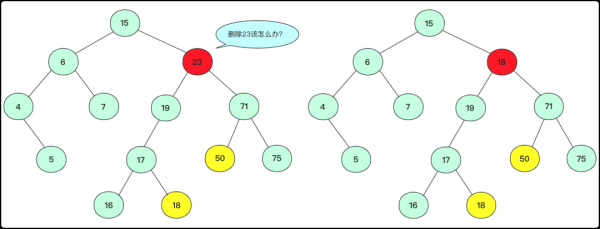
待刪除節點有兩個孩子
如果拿19或者71節點填補。雖然可以保證部分側大于小于該節點,但是會引起合并的混亂.比如你若用71替代23節點。那么你需要考慮三個節點(19,50,75)之間如何處理,還要考慮他們是否滿,是否有子女,這是個復雜的過程,不適合考慮。
所以,我們要分析我們要的這個點的屬性:能夠保證該點在這個位置仍滿足二叉搜索樹的性質(找到值最近的),那么子樹中哪個節點滿足這樣的關系呢?
左子樹中最右側節點或者右子樹中最左側節點都滿足,我們可以選一個節點將待刪除節點值替換掉(這里替換成左子樹最右側節點)。
這個點替換之后該怎么辦呢?很簡單啊,二叉樹用遞歸思路解決問題,再次調用刪除函數在左子樹中刪除替換的節點即可。
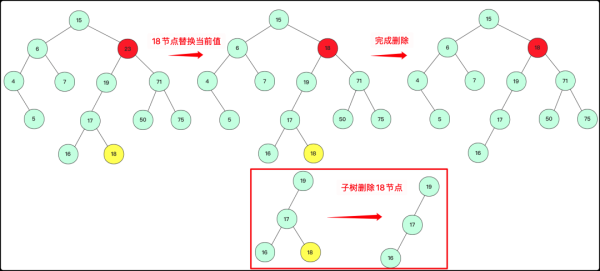
先替換值再遞歸在子樹中刪除18節點
這里演示是選取左子樹最大節點(最右側)替代,當然使用右子樹最小節點也能滿足在這待刪除的大小關系,原理一致。整個刪除算法流程為:
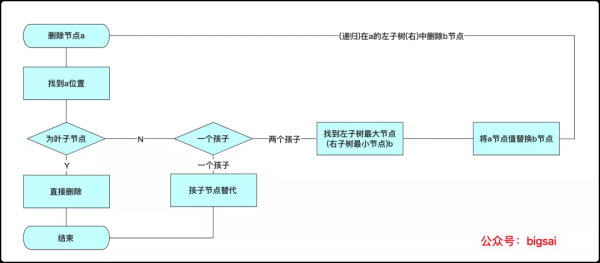
刪除流程
這部分操作的代碼為:
public node remove(int x, node t)// 刪除節點 { if (t == null) { return null; } if (x < t.value) { t.left = remove(x, t.left); } else if (x > t.value) { t.right = remove(x, t.right); } else if (t.left != null && t.right != null)// 左右節點均不空 { t.value = findmin(t.right).value;// 找到右側最小值替代 t.right = remove(t.value, t.right); } else // 左右單空或者左右都空 { if (t.left == null && t.right == null) { t = null; } else if (t.right != null) { t = t.right; } else if (t.left != null) { t = t.left; } return t; } return t; }這個完整代碼是筆者在大三時候寫的,可能有不少疏漏或者不規范的地方,僅供學習參考,如有疏漏錯誤還請指正。
二叉排序樹完整代碼為:
到此,相信大家對“何為二叉搜索樹”有了更深的了解,不妨來實際操作一番吧!這里是億速云網站,更多相關內容可以進入相關頻道進行查詢,關注我們,繼續學習!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。