前端算法系統練習之怎么掌握鏈表

這篇文章主要講解了“前端算法系統練習之怎么掌握鏈表”，文中的講解內容簡單清晰，易于學習與理解，下面請大家跟著小編的思路慢慢深入，一起來研究和學習“前端算法系統練習之怎么掌握鏈表”吧！

在練習之前，首先闡明一下我的觀點，以免大家對數據結構和算法或者這個系列產生更多的誤解。

我想各位當中肯定有準備面試的同學，那么你肯定聽說過面試造火箭，工作擰螺絲, 不少人也拿這句話拿來詬病當前一些互聯網大廠的算法面試，因此就有這樣的言論:  除了應付面試，學算法其實沒啥用。

這句話我并不完全反對，因為現在隨著技術生態的發展，各位走在領域前沿的大牛們已經給大家備足了輪子，遇到一般的業務問題直接把人家的方案拿到用就可以了，另外我也看到過一句話，剛開始覺得扯淡，后來想想覺得有那么一絲道理:

凡是需要跨過一定智商門檻才能掌握的技術，都不會輕易的流行。

換句話說：技術變得更簡單，別人更愿意用，更容易流行。

這也是當前各種技術框架的真實寫照: 足夠好用，足夠簡單，簡單到你不需要知道底層復雜的細節。

那么問題來了，作為一個集智慧和才華于一身的程序員，自己的價值在哪里?

我覺得價值的大小取決于你能夠解決的問題，如果說照著設計稿畫出一個簡單的  Button，你能完成，別的前端也能完成，甚至后后端的同學都能把效果差不多做出來，那這個時候就談何個人價值?只不過在一個隨時可替代的崗位上完成了大多數人能輕易做到的事情，張三來完成，或者李四來完成，其實沒什么區別。

但是現在如果面對的是一個復雜的工程問題，需要你來開發一個輔助業務的腳手架工具，改造框架源碼來提高項目的擴展性，或者面對嚴重的性能問題能馬上分析出原因，然后給出解決的思路并在不同因素中平衡，這些都不是一個業余的玩家能夠在短時間內勝任的，這就是體現自己價值的地方。

回到算法本身，它代表的是你解決更加復雜問題能力的一部分。所以從長期來看，對我們的發展是有潛移默化的幫助的。我們接下來進入到鏈表的部分。主要分為下面這幾個主題:

反轉鏈表

反轉鏈表這里一共有三個題目供大家訓練。分別是原地單鏈表的反轉、兩個一組反轉鏈表和K個一組反轉鏈表，難度由階梯式上升。

而在面試當中凡是遇到鏈表，反轉類的題目出現的頻率也是數一數二的，因此把它當做鏈表開篇的訓練類型，希望大家能引起足夠的重視?。

NO.1 簡單的反轉鏈表

反轉一個單鏈表。

示例:

輸入: 1->2->3->4->5->NULL 輸出: 5->4->3->2->1->NULL

來源: LeetCode 第 206 題

循環解決方案

這道題是鏈表中的經典題目，充分體現鏈表這種數據結構操作思路簡單, 但是實現上并沒有那么簡單的特點。

那在實現上應該注意一些什么問題呢?

保存后續節點。作為新手來說，很容易將當前節點的  next指針直接指向前一個節點，但其實當前節點下一個節點的指針也就丟失了。因此，需要在遍歷的過程當中，先將下一個節點保存，然后再操作next指向。

鏈表結構聲定義如下:

function ListNode(val) {   this.val = val;   this.next = null; }

實現如下:

/**  * @param {ListNode} head  * @return {ListNode}  */ let reverseList =  (head) => {     if (!head)         return null;     let pre = null, cur = head;     while (cur) {         // 關鍵: 保存下一個節點的值         let next = cur.next;         cur.next = pre;         pre = cur;         cur = next;     }     return pre; };

由于邏輯比較簡單，代碼直接一氣呵成。不過僅僅寫完還不夠，對于鏈表問題，邊界檢查的習慣能幫助我們進一步保證代碼的質量。具體來說:

• 當 head 節點為空時，我們已經處理，通過?

• 當鏈表只包含一個節點時, 此時我們希望直接返回這個節點，對上述代碼而言，進入循環后 pre 被賦值為cur，也就是head，沒毛病，通過?

運行在 LeetCode, 成功 AC ?

但作為系統性的訓練而言，單單讓程序通過未免太草率了，我們后續會盡可能地用不同的方式去解決相同的問題，達到融會貫通的效果，也是對自己思路的開拓，有時候或許能達到更優解。

遞歸解決方案

由于之前的思路已經介紹得非常清楚了，因此在這我們貼上代碼，大家好好體會：

let reverseList = (head) =>{   let reverse = (pre, cur) => {     if(!cur) return pre;     // 保存 next 節點     let next = cur.next;     cur.next = pre;     return reverse(cur, next);   }   return reverse(null, head); }

No.2 區間反轉

反轉從位置 m 到 n 的鏈表。請使用一趟掃描完成反轉。

說明:1 ≤ m ≤ n ≤ 鏈表長度。

示例:

輸入: 1->2->3->4->5->NULL, m = 2, n = 4 輸出: 1->4->3->2->5->NULL

來源: LeetCode 第 92 題

思路

這一題相比上一個整個鏈表反轉的題，其實是換湯不換藥。我們依然有兩種類型的解法：循環解法和遞歸解法。

需要注意的問題就是前后節點的保存(或者記錄)，什么意思呢?看這張圖你就明白了。

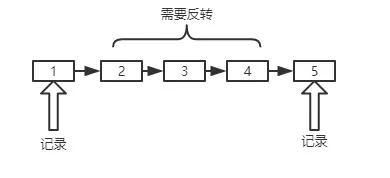
關于前節點和后節點的定義，大家在圖上應該能看的比較清楚了，后面會經常用到。

反轉操作上一題已經拆解過，這里不再贅述。值得注意的是反轉后的工作，那么對于整個區間反轉后的工作，其實就是一個移花接木的過程，首先將前節點的 next  指向區間終點，然后將區間起點的 next 指向后節點。因此這一題中有四個需要重視的節點:  前節點、后節點、區間起點和區間終點。接下來我們開始實際的編碼操作。

循環解法

/**  * @param {ListNode} head  * @param {number} m  * @param {number} n  * @return {ListNode}  */ var reverseBetween = function(head, m, n) {     let count = n - m;     let p = dummyHead = new ListNode();     let pre, cur, start, tail;     p.next = head;     for(let i = 0; i < m - 1; i ++) {         p = p.next;     }     // 保存前節點     front = p;     // 同時保存區間首節點     pre = tail = p.next;     cur = pre.next;     // 區間反轉     for(let i = 0; i < count; i++) {         let next = cur.next;         cur.next = pre;         pre = cur;         cur = next;     }     // 前節點的 next 指向區間末尾     front.next = pre;     // 區間首節點的 next 指向后節點(循環完后的cur就是區間后面第一個節點，即后節點)     tail.next = cur;     return dummyHead.next; };

遞歸解法

對于遞歸解法，唯一的不同就在于對于區間的處理，采用遞歸程序進行處理，大家也可以趁著復習一下遞歸反轉的實現。

var reverseBetween = function(head, m, n) {   // 遞歸反轉函數   let reverse = (pre, cur) => {     if(!cur) return pre;     // 保存 next 節點     let next = cur.next;     cur.next = pre;     return reverse(cur, next);   }   let p = dummyHead = new ListNode();   dummyHead.next = head;   let start, end; //區間首尾節點   let front, tail; //前節點和后節點   for(let i = 0; i < m - 1; i++) {     p = p.next;   }   front = p; //保存前節點   start = front.next;   for(let i = m - 1; i < n; i++) {     p = p.next;   }   end = p;   tail = end.next; //保存后節點   end.next = null;   // 開始穿針引線啦，前節點指向區間首，區間首指向后節點   front.next = reverse(null, start);   start.next = tail;   return dummyHead.next; }

No.3 兩個一組翻轉鏈表

給定一個鏈表，兩兩交換其中相鄰的節點，并返回交換后的鏈表。

你不能只是單純的改變節點內部的值，而是需要實際的進行節點交換。

來源: LeetCode 第 24 題

示例:

給定 1->2->3->4, 你應該返回 2->1->4->3.

思路

如圖所示，我們首先建立一個虛擬頭節點(dummyHead)，輔助我們分析。

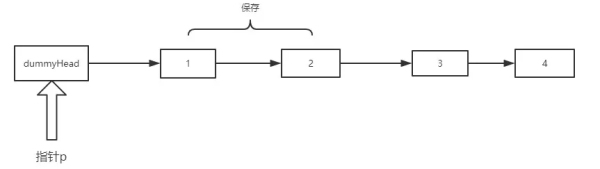
首先讓 p 處在 dummyHead 的位置，記錄下 p.next 和 p.next.next 的節點，也就是 node1 和 node2。

隨后讓 node1.next = node2.next, 效果:

然后讓 node2.next = node1, 效果:

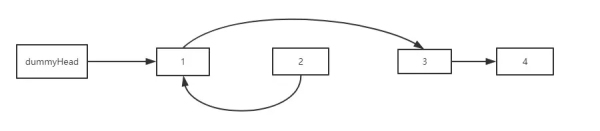
最后，dummyHead.next = node2，本次翻轉完成。同時 p 指針指向node1, 效果如下：

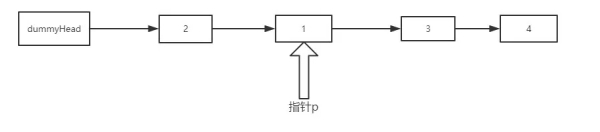
依此循環，如果 p.next 或者 p.next.next 為空，也就是找不到新的一組節點了，循環結束。

循環解決

思路清楚了，其實實現還是比較容易的，代碼如下:

var swapPairs = function(head) {     if(head == null || head.next == null)          return head;     let dummyHead = p = new ListNode();     let node1, node2;     dummyHead.next = head;     while((node1 = p.next) && (node2 = p.next.next)) {         node1.next = node2.next;         node2.next = node1;         p.next = node2;         p = node1;     }     return dummyHead.next; };

遞歸方式

var swapPairs = function(head) {     if(head == null || head.next == null)         return head;     let node1 = head, node2 = head.next;     node1.next = swapPairs(node2.next);     node2.next = node1;     return node2; };

利用遞歸方式之后，是不是感覺代碼特別簡潔????

希望你能好好體會一下遞歸調用的過程，相信理解之后對自己是一個很大的提升。

No.4 K個一組翻轉鏈表

給你一個鏈表，每 k 個節點一組進行翻轉，請你返回翻轉后的鏈表。

k 是一個正整數，它的值小于或等于鏈表的長度。

如果節點總數不是 k 的整數倍，那么請將最后剩余的節點保持原有順序。

示例 :

給定這個鏈表：1->2->3->4->5 當 k = 2 時，應當返回: 2->1->4->3->5 當 k = 3 時，應當返回: 3->2->1->4->5

說明 :

• 你的算法只能使用常數的額外空間。

• 你不能只是單純的改變節點內部的值，而是需要實際的進行節點交換。

來源: LeetCode 第 25 題

思路

思路類似No.3中的兩個一組翻轉。唯一的不同在于兩個一組的情況下每一組只需要反轉兩個節點，而在 K 個一組的情況下對應的操作是將 K  個元素的鏈表進行反轉。

遞歸解法

這一題我覺得遞歸的解法更容易理解，因此，先貼上遞歸方法的代碼。

• 以下代碼的注釋中`首節點`、`尾結點`等概念都是針對反轉前的鏈表而言的。

/**  * @param {ListNode} head  * @param {number} k  * @return {ListNode}  */ var reverseKGroup = function(head, k) {     let pre = null, cur = head;     let p = head;     // 下面的循環用來檢查后面的元素是否能組成一組     for(let i = 0; i < k; i++) {         if(p == null) return head;         p = p.next;     }     for(let i = 0; i < k; i++){         let next = cur.next;         cur.next = pre;         pre = cur;         cur = next;     }     // pre為本組最后一個節點，cur為下一組的起點     head.next = reverseKGroup(cur, k);     return pre; };

循環解法

重點都放在注釋里面了。

var reverseKGroup = function(head, k) {     let count = 0;     // 看是否能構成一組，同時統計鏈表元素個數     for(let p = head; p != null; p = p.next) {         if(p == null && i < k) return head;         count++;     }     let loopCount = Math.floor(count / k);     let p = dummyHead = new ListNode();     dummyHead.next = head;     // 分成了 loopCount 組，對每一個組進行反轉     for(let i = 0; i < loopCount; i++) {         let pre = null, cur = p.next;         for(let j = 0; j < k; j++) {             let next = cur.next;             cur.next = pre;             pre = cur;             cur = next;         }         // 當前 pre 為該組的尾結點，cur 為下一組首節點         let start = p.next;// start 是該組首節點         // 開始穿針引線！思路和2個一組的情況一模一樣         p.next = pre;         start.next = cur;         p = start;     }     return dummyHead.next; };

環形鏈表

NO.1 如何檢測鏈表形成環?

給定一個鏈表，判斷鏈表中是否形成環。

思路

思路一: 循環一遍，用 Set 數據結構保存節點，利用節點的內存地址來進行判重，如果同樣的節點走過兩次，則表明已經形成了環。

思路二: 利用快慢指針，快指針一次走兩步，慢指針一次走一步，如果兩者相遇，則表明已經形成了環。

可能你會納悶，為什么思路二用兩個指針在環中一定會相遇呢?

其實很簡單，如果有環，兩者一定同時走到環中，那么在環中，選慢指針為參考系，快指針每次相對參考系向前走一步，終究會繞回原點，也就是回到慢指針的位置，從而讓兩者相遇。如果沒有環，則兩者的相對距離越來越遠，永遠不會相遇。

接下來我們來編程實現。

方法一: Set 判重

/**  * @param {ListNode} head  * @return {boolean}  */ var hasCycle = (head) => {     let set = new Set();     let p = head;     while(p) {         // 同一個節點再次碰到，表示有環         if(set.has(p)) return true;         set.add(p);         p = p.next;     }     return false; }

方法二: 快慢指針

var hasCycle = function(head) {     let dummyHead = new ListNode();     dummyHead.next = head;     let fast = slow = dummyHead;     // 零個結點或者一個結點，肯定無環     if(fast.next == null || fast.next.next == null)          return false;     while(fast && fast.next) {         fast = fast.next.next;         slow = slow.next;         // 兩者相遇了         if(fast == slow) {             return true;         }     }      return false; };

No.2 如何找到環的起點

給定一個鏈表，返回鏈表開始入環的第一個節點。 如果鏈表無環，則返回 null。

**說明：**不允許修改給定的鏈表。

思路分析

剛剛已經判斷了如何判斷出現環，那如何找到環的節點呢?我們來分析一波。

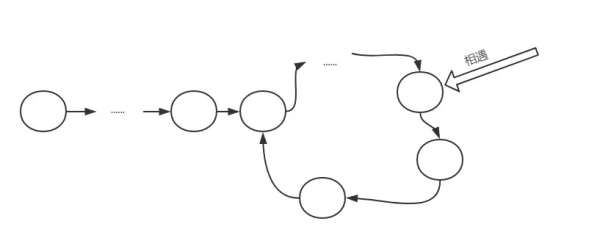
看上去比較繁瑣，我們把它做進一步的抽象:

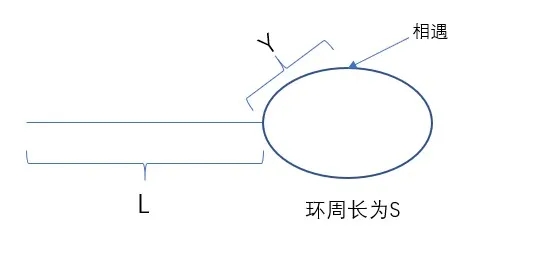
設快慢指針走了x秒，慢指針一秒走一次。

對快指針，有: 2x - L = m * S + Y -----①

對慢指針，有: x - L = n * S + Y -----②

其中，m、n 均為自然數。

① - ② * 2 得:

L = (m - n) * S - Y-----③

好，這是一個非常重要的等式。我們現在假設有一個新的指針在 L 段的最左端，慢指針現在還在相遇處。

讓新指針和慢指針都每次走一步，那么，當新指針走了 L 步之后到達環起點，而與此同時，我們看看慢指針情況如何。

由③式，慢指針走了(m - n) * S - Y個單位，以環起點為參照物，相遇時的位置為 Y，而現在由Y + (m - n) * S - Y即(m -  n) * S，得知慢指針實際上參照環起點，走了整整(m - n)圈。也就是說，慢指針此時也到達了環起點。:::tip 結論  現在的解法就很清晰了，當快慢指針相遇之后，讓新指針從頭出發，和慢指針同時前進，且每次前進一步，兩者相遇的地方，就是環起點。:::

編程實現

懂得原理之后，實現起來就容易很多了。

/**  * @param {ListNode} head  * @return {ListNode}  */ var detectCycle = function(head) {     let dummyHead = new ListNode();     dummyHead.next = head;     let fast = slow = dummyHead;     // 零個結點或者一個結點，肯定無環     if(fast.next == null || fast.next.next == null)          return null;     while(fast && fast.next) {         fast = fast.next.next;         slow = slow.next;         // 兩者相遇了         if(fast == slow) {            let p = dummyHead;            while(p != slow) {                p = p.next;                slow = slow.next;            }            return p;         }     }      return null; };

鏈表合并

NO.1 合并兩個有序鏈表

將兩個有序鏈表合并為一個新的有序鏈表并返回。新鏈表是通過拼接給定的兩個鏈表的所有節點組成的。

示例:

輸入：1->2->4, 1->3->4 輸出：1->1->2->3->4->4

來源: LeetCode第21題

遞歸解法

遞歸解法更容易理解，我們先用遞歸來做一下:

/**  * @param {ListNode} l1  * @param {ListNode} l2  * @return {ListNode}  */ var mergeTwoLists = function(l1, l2) {     const merge = (l1, l2) => {         if(l1 == null) return l2;         if(l2 == null) return l1;         if(l1.val > l2.val) {             l2.next = merge(l1, l2.next);             return l2;         }else {             l1.next = merge(l1.next, l2);             return l1;         }     }     return merge(l1, l2); };

循環解法

var mergeTwoLists = function(l1, l2) {     if(l1 == null) return l2;     if(l2 == null) return l1;     let p = dummyHead = new ListNode();     let p1 = l1, p2 = l2;     while(p1 && p2) {         if(p1.val > p2.val) {             p.next = p2;             p = p.next;             p2 = p2.next;         }else {             p.next = p1;             p = p.next;             p1 = p1.next;         }     }     // 循環完成后務必檢查剩下的部分     if(p1) p.next = p1;     else p.next = p2;     return dummyHead.next; };

No.2 合并 K 個有序鏈表

合并 k 個排序鏈表，返回合并后的排序鏈表。請分析和描述算法的復雜度。

示例:

輸入: [   1->4->5,   1->3->4,   2->6 ] 輸出: 1->1->2->3->4->4->5->6

來源: LeetCode第23題

自上而下(遞歸)實現

/**  * @param {ListNode[]} lists  * @return {ListNode}  */ var mergeKLists = function(lists) {     // 上面已經實現     var mergeTwoLists = function(l1, l2) {/*上面已經實現*/};     const _mergeLists = (lists, start, end) => {         if(end - start < 0) return null;         if(end - start == 0)return lists[end];         let mid = Math.floor(start + (end - start) / 2);         return mergeTwoList(_mergeLists(lists, start, mid), _mergeLists(lists, mid + 1, end));     }     return _mergeLists(lists, 0, lists.length - 1); };

自下而上實現

在這里需要提醒大家的是，在自下而上的實現方式中，我為每一個鏈表綁定了一個虛擬頭指針(dummyHead)，為什么這么做?

這是為了方便鏈表的合并，比如 l1 和 l2 合并之后，合并后鏈表的頭指針就直接是 l1 的 dummyHead.next 值，等于說兩個鏈表都合并到了  l1 當中，方便了后續的合并操作。

var mergeKLists = function(lists) {     var mergeTwoLists = function(l1, l2) {/*上面已經實現*/};     // 邊界情況     if(!lists || !lists.length) return null;     // 虛擬頭指針集合     let dummyHeads = [];     // 初始化虛擬頭指針     for(let i = 0; i < lists.length; i++) {         let node = new ListNode();         node.next = lists[i];         dummyHeads[i] = node;     }     // 自底向上進行merge     for(let size = 1; size < lists.length; size += size){         for(let i = 0; i + size < lists.length;i += 2 * size) {             dummyHeads[i].next = mergeTwoLists(dummyHeads[i].next, dummyHeads[i + size].next);         }     }     return dummyHeads[0].next; };

多個鏈表的合并到這里就實現完成了，在這里順便告訴你這種歸并的方式同時也是對鏈表進行歸并排序的核心代碼。希望你能好好體會自上而下和自下而上兩種不同的實現細節，相信對你的編程內功是一個不錯的提升。

求鏈表中間節點

判斷回文鏈表

請判斷一個單鏈表是否為回文鏈表。

示例1:

輸入: 1->2 輸出: false

示例2:

輸入: 1->2->2->1 輸出: true

你能否用 O(n) 時間復雜度和 O(1) 空間復雜度解決此題?

來源: LeetCode第234題

思路分析

這一題如果不考慮性能的限制，其實是非常簡單的。但考慮到 O(n) 時間復雜度和 O(1) 空間復雜度，恐怕就值得停下來好好想想了。

題目的要求是單鏈表，沒有辦法訪問前面的節點，那我們只得另辟蹊徑:

找到鏈表中點，然后將后半部分反轉，就可以依次比較得出結論了。下面我們來實現一波。

代碼實現

其實關鍵部分的代碼就是找中點了。先亮劍:

let dummyHead = slow = fast = new ListNode(); dummyHead.next = head; // 注意注意，來找中點了 while(fast && fast.next) {     slow = slow.next;     fast = fast.next.next; }

你可能會納悶了，為什么邊界要設成這樣?

我們不妨來分析一下，分鏈表節點個數為奇數和偶數的時候分別討論。

當鏈表節點個數為奇數

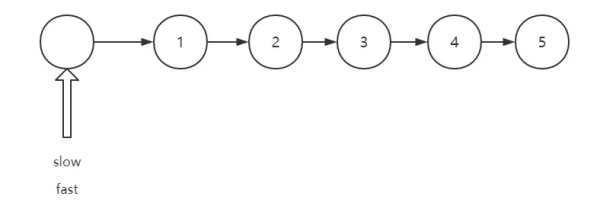
試著模擬一下， fast 為空的時候，停止循環, 狀態如下:

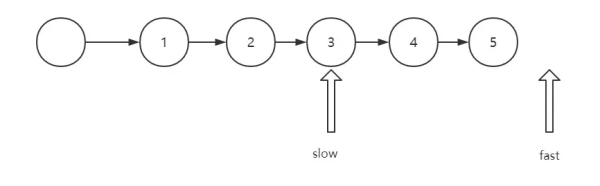
當鏈表節點個數為偶數

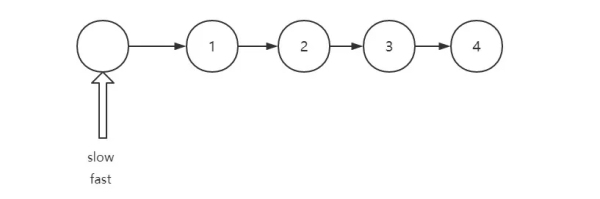
模擬走一遍，當 fast.next  為空的時候，停止循環，狀態如下:

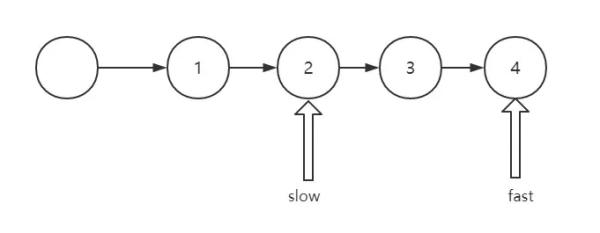
對于 fast 為空和fast.next為空兩個條件，在奇數的情況下，總是 fast為空先出現，偶數的情況下，總是fast.next先出現.

也就是說: 一旦fast為空, 鏈表節點個數一定為奇數，否則為偶數。因此兩種情況可以合并來討論，當 fast 為空或者 fast.next  為空，循環就可以終止了。

完整實現如下:

/**  * @param {ListNode} head  * @return {boolean}  */ var isPalindrome = function(head) {     let reverse = (pre, cur) => {         if(!cur) return pre;         let next = cur.next;         cur.next = pre;         return reverse(cur, next);     }     let dummyHead = slow = fast = new ListNode();     dummyHead.next = head;     // 注意注意，來找中點了, 黃金模板     while(fast && fast.next) {         slow = slow.next;         fast = fast.next.next;     }     let next = slow.next;     slow.next = null;     let newStart = reverse(null, next);     for(let p = head, newP = newStart; newP != null; p = p.next, newP = newP.next) {         if(p.val != newP.val) return false;     }     return true; };

感謝各位的閱讀，以上就是“前端算法系統練習之怎么掌握鏈表”的內容了，經過本文的學習后，相信大家對前端算法系統練習之怎么掌握鏈表這一問題有了更深刻的體會，具體使用情況還需要大家實踐驗證。這里是億速云，小編將為大家推送更多相關知識點的文章，歡迎關注！