您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
本篇內容主要講解“RSA-PSS 算法的原理和應用”,感興趣的朋友不妨來看看。本文介紹的方法操作簡單快捷,實用性強。下面就讓小編來帶大家學習“RSA-PSS 算法的原理和應用”吧!
AS(5):RSA-PSS 算法簡介
2018年發布的 TLS v1.3(TLS:Transport Layer Security,傳輸安全層協議,TLS v1.3 對應 RFC 8446)中,其支持的數字簽名算法有:RSASSA-PKCS1-v1_5、RSASSA-PSS、ECDSA(Elliptic Curve Digital Signature Algorithm,橢圓曲線簽名算法)、EdDSA(Edwards-Curve Digital Signature Algorithm,愛德華曲線簽名算法)。
這些算法已經是標準(或者是事實上的標準),不過從某種意義上說,這些算法也代表著美國簽名算法流派。
除美國外,俄羅斯在1994年發布數字簽名算法標準 GOST R 34.10-94,并在2001年發布橢圓曲線數字簽名算法標準GOST R34.10- 2001。GOST R34.10-2001在2012年更新為 GOST R34.10-2012。韓國在1998年發表韓國基于證書的數字簽名算法 KCDSA 和 EC- KCDA,對應標準發布于[88,89]。德國在 2005 年發布德國橢圓曲線數字簽名算法標準 EC- GDSA。中國在 2012 年發布 SM2 橢圓曲線數字簽名算法標準,在 2016 年發布 SM9 標識密碼數字簽名算法標準。
作為重要的國際標準化組織,ISO/IEC 同樣也發布了一系列的數字簽名算法標準:ISO/IEC 9796、ISO/ IEC 14888、ISO/IEC 20008、ISO/IEC 18370、ISO/IEC 23264 等等。
弱水三千,只取一瓢。由于文章主題和篇幅的關系,本文只介紹 RSASA-PSS 算法。
PSS (Probabilistic Signature Scheme,概率簽名方案)是私鑰簽名的一種填充方式。RSASA(RSA Signature Algorithm,RSA 數字簽名算法)目前支持兩種算法:RSASSA-PKCS1-v1_5、RSASSA-PSS。由于安全的原因,RSASSA-PKCS1-v1_5 現在的使用場景僅僅是為了兼容(可以參考《童話里都是騙人的》、《夢被批得離離散散》、《蜀道難,難于上青天》),當前主流推薦使用 RSASSA-PSS 算法。
PSS 方案首先由 Bellare和Rogaway 首先提出,PSS 與 OAEP(Optimal Asymmetric Encryption Padding,最優非對稱加密填充)非常相像,當然 OAEP也是由這兩位大神提出的(OAEP 請參見《蜀道難,難于上青天》)。
Mihir Bellare是加州大學圣地亞哥分校(UCSD,University of California, San Diego)計算機科學與工程系的教授。Bellare 于1986年在加州理工學院獲得學士學位,1991年在麻省理工學院獲得博士學位。1991年至1995年,Bellare 在IBM擔任研究員 Bellare 是HMAC、RSA-OAEP、RSA-PSS和OCB的聯合開發者。Bellare 是 ACM 和 IACR 的研究員。他曾獲得 ACM 巴黎Kanellakis 理論與實踐獎,RSA 會議數學獎,David 和 Lucille Packard基金會科學與工程獎學金,以及NSF職業獎( He has received an ACM Paris Kanellakis Theory and Practice Award, an RSA Conference Award in Mathematics, a David and Lucille Packard Foundation Fellowship in Science and Engineering, and an NSF Career award)。
Phillip Rogaway 是美國加州大學戴維斯分校(UCD,University of California, Davis)計算機科學系的教授。Rogaway 本科畢業于加州大學伯克利分校(UCB,University of California, Berkeley),并于1991年到麻省理工計算理論小組攻讀博士學位(MIT s Theory of Computation group )。博士畢業之后,Rogaway 到 IBM 擔任安全架構師,然后于1994年到 UCD 工作。Rogaway 獲得過 Levchin 獎(2016),PET 獎(2015),IACR 研究員(2012),ACM巴黎 Kanellakis 獎(2009),RSA 數學獎(2003)(Levchin prize (2016), PET Award (2015), IACR Fellow (2012), ACM Paris Kanellakis Award (2009), RSA Award in Mathematics (2003))。

圖1 Bellare(左)和 Rogaway(右)
RSA 數字簽名算法(RSASA)的本質,仍然是 RSA 加密/解密算法,如圖2所示。
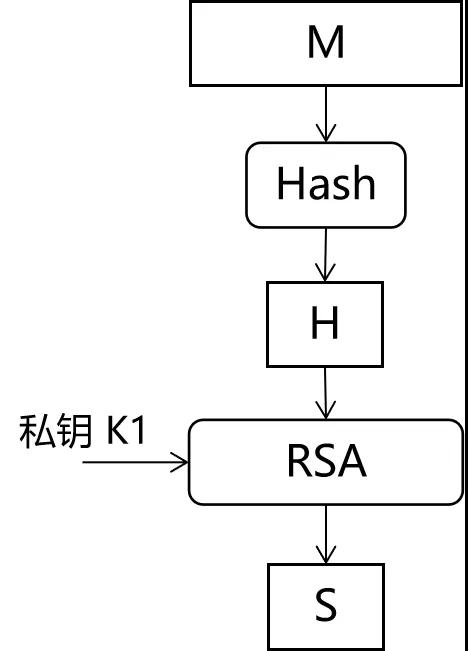
圖2 RSA 數字簽名算法示意
從圖2可以看到,RSSSA 分為兩步。
1)將待簽名的 M 進行 Hash,從而得到 H
2)將 H 進行 RSA 私鑰加密
既然是 RSA 加密,就繞不開 RSA 那個致命問題——能夠非常簡單地被選擇密文攻擊所破解(具體請參見《童話里都是騙人的》),于是也就引發了 RSA 填充算法。
RSASSA-PKCS1-v1_5 采用的就是 RSA_PKCS1_PADDING_v1_5 填充算法,而 RSASSA-PSS 的填充算法則與 RSA_PKCS1_OAEP_PADDING 填充算法比較相像。下面我們就介紹 RSASSA-PSS 算法。
RSASSA-PSS 算法本質就是在 RSA 算法的基礎上疊加上一種填充算法(為了便于表述,這種填充算法也可以稱為 RSA-PSS 填充算法,或者 RSA-PSS 編碼),如圖3所示。
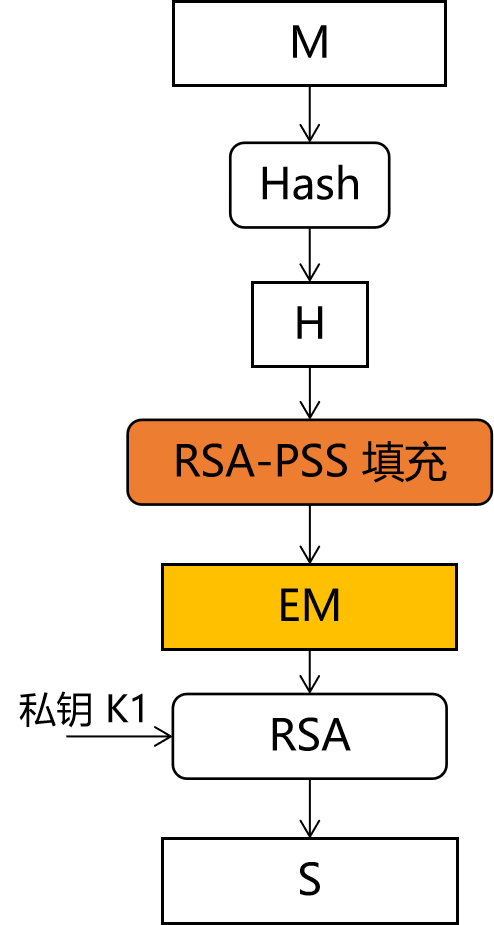
圖3 RSA-PSS 數字簽名算法示意
圖3中,在 Hash 之后,在 RSA 之前,RSASA-PSS 算法插入了一個 RSA-PSS 填充算法。RSA-PSS 的具體算法,如圖4所示。
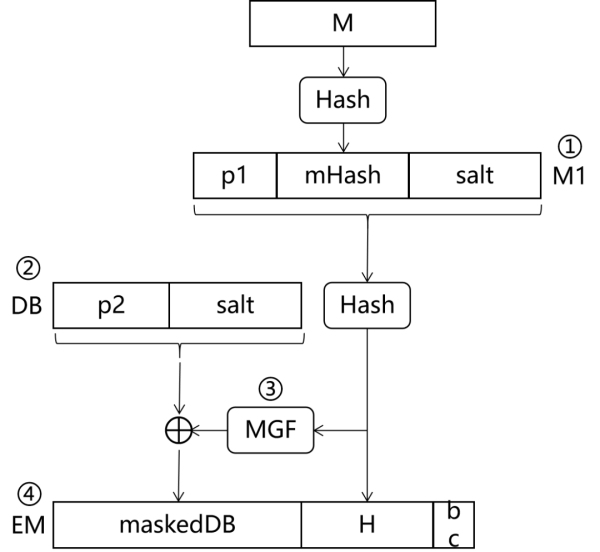
圖4 RSA-PSS 填充算法示意
圖4中,RSA-PSS 填充算法,分為四步。下面我們分別講述這四步。
1.1 M 轉換成 M1
通過圖4可以看到,
M1 = p1 || mHash || salt
p1 就是8字節的0。
mHash = Hash(M),M 是待簽名的消息,Hash 算法當前的選擇是 SHA-1。SHA-1 的輸出是20個字節,所以 mHash 的長度
hLen = 20
salt(鹽值)就是一個偽隨機數,它的長度(記為 sLen)一般等于 hLen,當前的選擇就是
sLen = hLen
1.2 構建 DB
DB(Data Block)的構建方式為,
DB = p2 || salt
p2 的值等于若干個字節的 0x00 后面跟著1字節的 0x01。這若干個字節記為 xLen,則 xLen 等于,
xLen = emLen - sLen - hLen - 2
其中,emLen 是圖4中 EM 的長度
salt 的值等于1.1節所描述的 salt 的值。特別強調,兩者必須相等,否則無法驗證數字簽名(具體請參見下面第三節:RSASSA-PSS 的數字簽名驗證)
1.3 MGF
MGF(Mask Generation Function,掩碼生成函數)的相關介紹,請參見《蜀道難,難于上青天》,這里就不再重復。另外,RSA-PSS 所采用的 MGF 函數的輸出,也是 MGF1。
對于圖4而言,MGF 所對應的輸入和輸出分別是
mask = MGF1(mgfSeed, maskLen, hash)
其中,
mgfSeed = Hash(M1),Hash 函數選擇 SHA-1
maskLen = emLen - hLen - 1
hash 函數選擇 SHA-1
1.4 構建 EM
EM(Encoded Message)的值等于,
EM = maskedDB || H || bc
其中,
maskedDB = DB xor mask
H = Hash(M1)
bc = 0xBC
其中,bc 的長度是1個字節,H 的長度是 hLen,maskedDB 的長度(記為 mdbLen)為
mdbLen = emLen - hLen - 1
其中,emLen 的長度就是 EM 的長度。由于接下來要對 EM 進行 RSA 加密計算,所以 EM 的長度滿足 RSA 的要求即可。
EM = RSA-PSS(M)
S = RSAEP(EM)
RSA 算法,請參見《RSA 基本算法》、《RSA 的計算方法》,這里不再重復。
RSASA-PSS 簽名驗證,分為如下幾個步驟。
3.1 解密
RSASA-PSS 的簽名驗證,首先是解密,
EM = RSADP(S)
也即,拿到簽名 S 以后,運行 RSA 解密算法,得到解密后的信息 EM。
3.2 分割 EM
得到 EM 以后,接下來就是分割和驗證,
maskedDB, H, bc = Split(EM)
最右一個字節是 bc,然后從 bc 往左數 hLen 個字節是 H,然后剩下的是 maskedDB。
如果最右一個字節不是 0xBC,則簽名驗證停止(該數字簽名是非法的)。
3.3 計算 salt
得到 H 以后,就可以計算 mask,
mask = MGF1(H, maskLen, hash)
因為,
maskedDB = DB xor mask
所以,
DB = maskedDB xor mask
得到 DB 以后,就可以對其分割
p2, salt = Split(DB)
其中,salt 是 DB 的最右 sLen 個字節,剩下的是 p2。
如果 p2 的值不等于若干個字節的 0x00 后面跟著1字節的 0x01,那么驗證停止(該數字簽名是非法的)。
3.4 校驗 Hash
通過所接收到的 M,計算 Hash
mHash = Hash(M)
然后構建 M1
M1 = p1 || mHash || salt
其中,salt 就是 3.3 步所計算出的 salt
再然后,計算 M1 的 Hash
H1 = Hash(M1)
比較 H1 與 H,如果兩者相等,則簽名驗證通過。如果不相等,則簽名非法。
其中,H 就是3.2步所得到的哈希值。
經過以上四步以后,就完成了 RSASA-PSS 的數字簽名驗證。
到此,相信大家對“RSA-PSS 算法的原理和應用”有了更深的了解,不妨來實際操作一番吧!這里是億速云網站,更多相關內容可以進入相關頻道進行查詢,關注我們,繼續學習!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。