您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
這篇文章主要介紹“什么是二分搜索樹”,在日常操作中,相信很多人在什么是二分搜索樹問題上存在疑惑,小編查閱了各式資料,整理出簡單好用的操作方法,希望對大家解答”什么是二分搜索樹”的疑惑有所幫助!接下來,請跟著小編一起來學習吧!
樹是一種很特別的數據結構,樹這種數據結構叫做 “樹” 就是因為它 長得像一棵樹 。但是這棵樹畫成的圖長得卻是一棵倒著的樹,根在上,葉在下。樹是圖的一種,樹和圖的區別就在于:樹是沒有環的,而圖是可以有環的。
樹狀圖是一種數據結構,它是由n(n>=1)個有限節點組成一個具有層次關系的集合。把它叫做“樹”是因為它看起來像一棵倒掛的樹,也就是說它是根朝上,而葉朝下的。
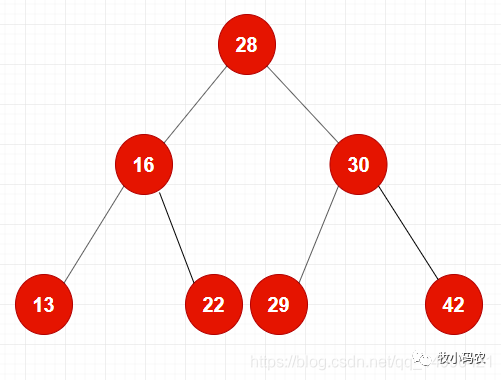
比如說電腦中的文件夾,我們需要找到一個特定的文件,需要到某個文件夾下去找這個文件,計算機的文件存儲的結構來源于生活。再比如說圖書館,我們知道圖書館里面有 歷史類、數理類、計算機類,我們想要找到關于java的書籍,就需要到計算機類的Java中去找到我們需要的圖書
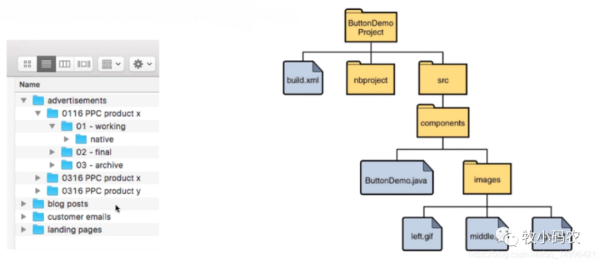
比如公司里面的層級結構:CEO、HR CTO等等,還有我們比較常見的家譜等等,都是類似于樹結構
將數據使用樹結構后,會更加的高效
二分搜索樹是一個動態數據結構
二分搜索樹也是一顆二叉樹(也叫多叉樹)
二分搜索樹的每個節點的值都大于其左子樹的所有節點的值,同時每個節點的值都小于其右子樹的所有節點的值
存儲的元素必須有可比較性, Java中的話就要求二分搜索樹保存的數據類型要實現Comparable接口, 或者使用額外的比較器實現
每一顆子樹也是二分搜索樹
二分搜索樹具有唯一根節點,同時在二叉樹中最底下是它的葉子節點
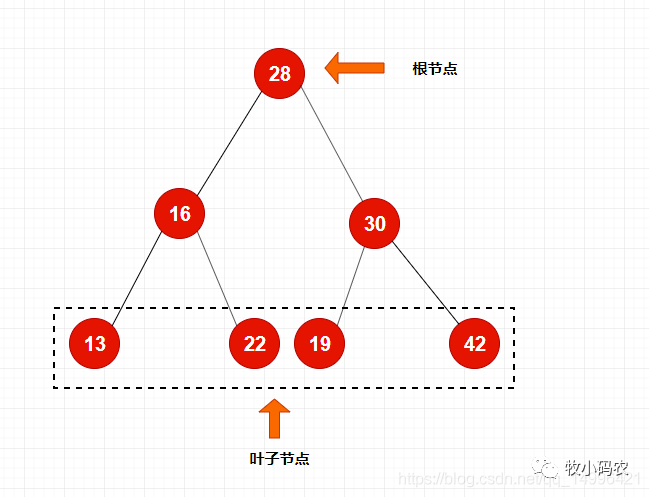
二分搜索樹具有唯根節點,每個節點最多有兩個孩子(左邊的叫左孩子,右邊的叫右孩子),同時每個節點最多有一個父親
每個節點的左子樹也是二叉樹
每個節點的右子樹也是二叉樹
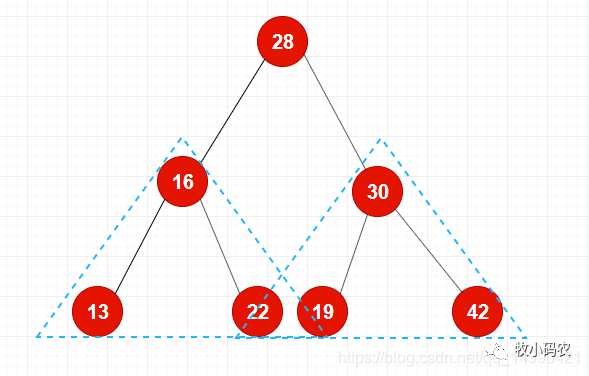
二叉樹不一定是滿的,一個接電腦也是二叉樹、空也是二叉樹
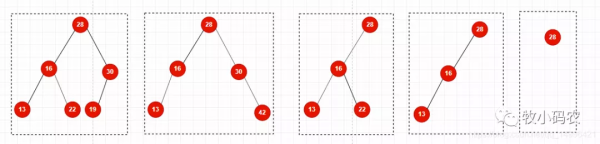
在進行相關操作之前, 先定義一個支持泛型的節點類, 用于存儲二分搜索樹每個節點的信息, 這個類作為二分搜索樹的一個內部類, 二分搜索樹的類聲明以及Node節點類聲明如下:
public class BST> { private class Node{ public E e; public Node left,right; public Node(E e){ this.e = e; left = null; right = null; } } //節點 private Node root; // 樹容量 private int size; public BST(){ root = null; size = 0; } public int size(){ return size; } public boolean isEmpty(){ return size == 0; } }二分搜索樹添加元素的非遞歸寫法,和鏈表很像,由于二分搜索樹本身的遞歸特性, 所以可以很方便的使用遞歸實現向二分搜索樹中添加元素,
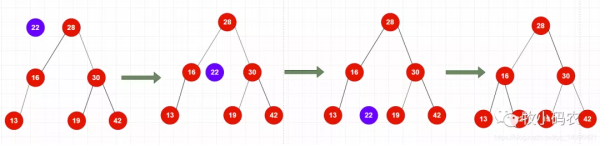
代碼實現:
//向二分搜索樹添加新的元素e public void add(E e){ root = add(root,e); } //向以Node為根的二分搜索樹中插入元素 E,遞歸算法 //返回插入新節點后二分搜索樹的根 private Node add(Node node,E e){ if(node == null){ size++; return new Node(e); } if(e.compareTo(node.e) < 0) node.left = add(node.left,e); else if(e.compareTo(node.e) > 0) node.right = add(node.right,e); return node; }由于二分搜索樹沒有下標, 所以針對二分搜索樹的查找操作, 我們需要定義一個 contains() 方法, 查看二分搜索樹是否包含某個元素, 返回一個布爾型變量
代碼實現:
//看二分是搜索樹中是否包含元素e public boolean contains(E e){ return contains(root,e); } //看以Node為根的二分搜索樹中是否包含元素e,遞歸算法 private boolean contains(Node node,E e){ if(node == null) return false; if(e.compareTo(node.e) == 0) return true; else if(e.compareTo(node.e) < 0) return contains(node.left,e); else //e.compareTo(node.e) > 0 return contains(node.right,e); }遍歷操作就是把所有的節點都訪問一遍
訪問的原因和業務相關
遍歷分類
前序遍歷 : 對當前節點的遍歷在對左右孩子節點的遍歷之前, 遍歷順序 : 當前節點->左孩子->右孩子中序遍歷 : 對當前節點的遍歷在對左右孩子節點的遍歷中間, 遍歷順序 : 左孩子->當前節點->右孩子后序遍歷 : 對當前節點的遍歷在對左右孩子節點的遍歷之后, 遍歷順序 : 左孩子->右孩子->當前節點
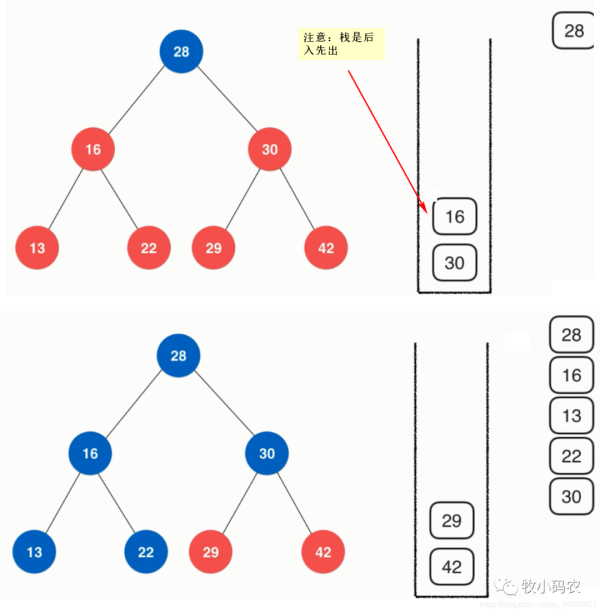
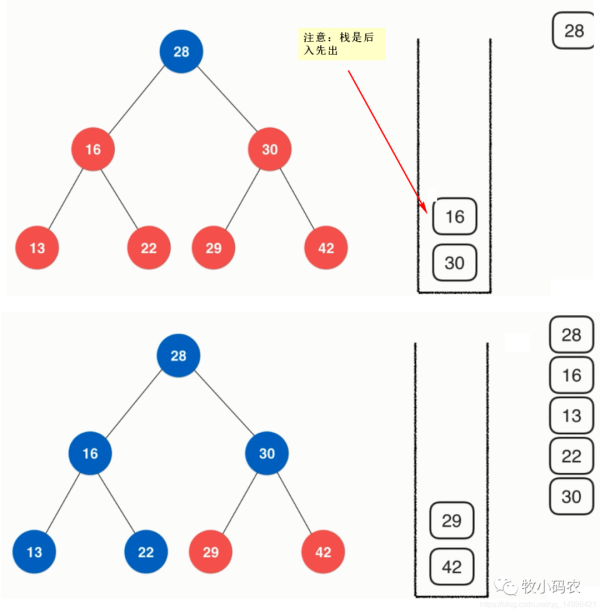
//二分搜索樹前序遍歷 public void preOrder(){ preOrder(root); } //前序遍歷以Node為根的二分搜索樹,遞歸算法 private void preOrder(Node node){ if(node == null) return; System.out.println(node.e); preOrder(node.left); preOrder(node.right); } public void preOrderNR(){ Stack stack = new Stack<>(); stack.push(root); while(!stack.isEmpty()){ Node cur = stack.pop(); System.out.println(cur.e); if(cur.right != null) stack.push(cur.right); if(cur.left != null) stack.push(cur.left); } }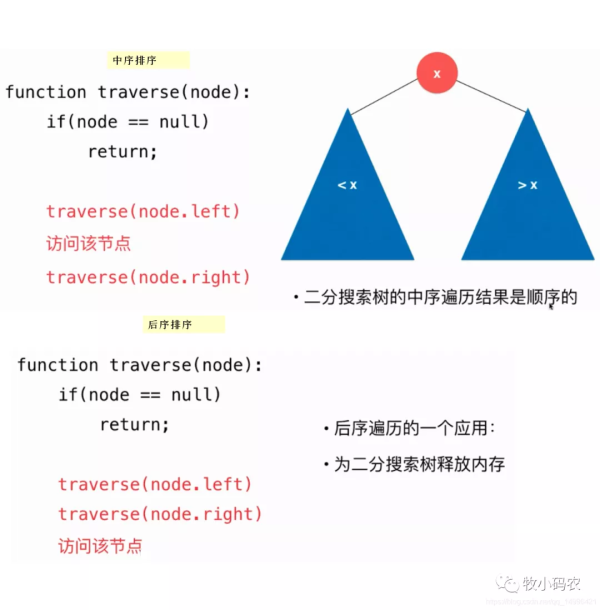
//二分搜索樹的中序遍歷 public void inOrder(){ inOrder(root); } //中序遍歷以Node為根的二分搜索樹,遞歸算法 private void inOrder(Node node){ if(node ==null) return; inOrder(node.left); System.out.println(node.e); inOrder(node.right); }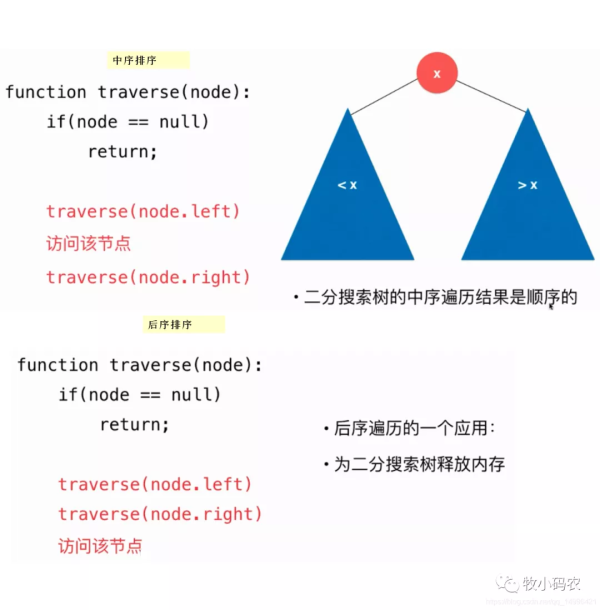
//二分搜索樹的后序遍歷 public void postOrder(){ inOrder(root); } public void levelOrder(){ Queue q = new LinkedList(); q.add(root); while (!q.isEmpty()){ Node cur = q.remove(); System.out.println(cur.e); if(cur.left != null) q.add(cur.left); if(cur.right != null) q.add(cur.right); } } //后序遍歷以Node為根的二分搜索樹,遞歸算法 private void postOrder(Node node){ if(node ==null) return; inOrder(node.left); inOrder(node.right); System.out.println(node.e); }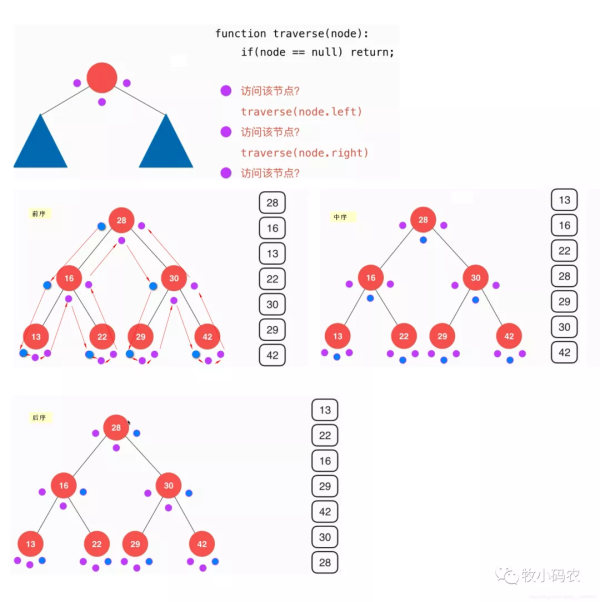
二分搜索樹前序非遞歸寫法
到此,關于“什么是二分搜索樹”的學習就結束了,希望能夠解決大家的疑惑。理論與實踐的搭配能更好的幫助大家學習,快去試試吧!若想繼續學習更多相關知識,請繼續關注億速云網站,小編會繼續努力為大家帶來更多實用的文章!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。