您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
本篇文章給大家分享的是有關什么是多路搜索樹B樹和B+樹,小編覺得挺實用的,因此分享給大家學習,希望大家閱讀完這篇文章后可以有所收獲,話不多說,跟著小編一起來看看吧。
多路搜索樹
完全二叉樹高度:O(log2N),其中2為對數
完全M路搜索樹的高度:O(logmN),其中M為對數,樹每層的節點數
M路搜索樹主要用于解決數據量大無法全部加載到內存的數據存儲。通過增加每層節點的個數和在每個節點存放更多的數據來在一層中存放更多的數據,從而降低樹的高度,在數據查找時減少磁盤訪問次數。
所以每層的節點數和每個節點包含的關鍵字越多,則樹的高度越矮。但是在每個節點確定數據就越慢,但是B樹關注的是磁盤性能瓶頸,所以在單個節點搜索數據的開銷可以忽略。
B樹
B樹是一種M路搜索樹,B樹主要用于解決M路搜索樹的不平衡導致樹的高度變高,跟二叉樹退化為鏈表導致性能問題一樣。B樹通過對每層的節點進行控制、調整,如節點分離,節點合并,一層滿時向上分裂父節點來增加新的層等操作來來保證該M路搜索樹的平衡。具體規則如下:
根節點的兒子樹個數在2到M之間,其他非葉子節點的兒子樹個數在M/2和M之間。如果兒子樹個數因為分裂超過了M則此時需要向上遞歸分裂父節點,當找到一個不需要再分裂的父節點則停止分裂。該分裂過程直到根節點,如果需要分裂根節點,則會產生兩個根,故需要創建一個新的根來將這兩個根作為兒子節點,此時樹的高度會增加1。
每個非葉子節點的關鍵字的值從左到右依次變大,第i個關鍵字代表子樹i+1中的最小關鍵字;(其中對于根節點來說i在1到(2到M)之間,其他非葉子節點則是1到(M/2到M)之間);
B樹的所有數據項都存放到葉子節點,非葉子節點不存放數據,非葉子節點只存放用于指示搜索方向的關鍵字,即索引。這樣有利于將更多的非葉子節點加載到內存中,方便進行數據查找;
所有葉子節點都在相同的深度并且每個葉子節點包含L/2到L項數據。
M和L的大小選擇
M為B樹的階數或者說是路數
L為每個葉子節點最多存放的數據項個數
在B樹中,每個節點都是一個磁盤區塊,所以需要根據磁盤區塊的大小來決定M和L。
磁盤區塊大小與M的計算
每個非葉子節點存放了關鍵字和指向兒子樹的指針,具體數量為:M階的B樹,每個非葉子節點存放了M-1個關鍵字和M個指向兒子樹的指針,故加入每個關鍵字的大小為8字節(如Java的long類型就是8字節),每個指針為4字節,則M階B樹的每個非一葉子節點需要:8 * (M-1) + 4 * M = 12M - 8個字節。
如果規定每個非葉子節點(磁盤區塊)占用內存不超過8K,即8192,則M最大為683,即683*12-8=8192。
葉子節點數據項個數L
假如每個數據項大小也是256字節,則由于磁盤區塊大小為8K,即8192個字節,而每個葉子節點可以存放L/2到L個數據項,所以每個葉子節點最多存放:8192/256=32個數據項,即L的大小為32。
一棵5階的B樹的結構如下,即M和L等于5:其中每個非葉子節點包含最多M-1=5-1=4個關鍵字,包含M,即5個指向子樹指針。L等于5,則每個葉子節點最多存放5個數據項。
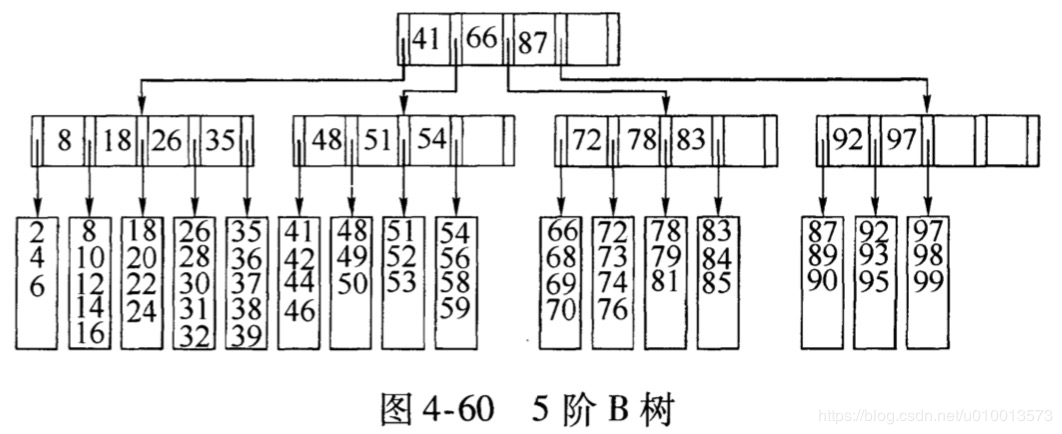
B+樹
B+樹結構跟B樹基本一致,唯一的區別是B+樹的葉子節點之間通過指針相連形成一個鏈表,故便于遍歷所有的葉子節點,即獲取所有或者搜索關鍵字某一范圍的所有數據項。MySQL的InnoDB存儲引擎就是會用B+樹作為索引實現。
以上就是什么是多路搜索樹B樹和B+樹,小編相信有部分知識點可能是我們日常工作會見到或用到的。希望你能通過這篇文章學到更多知識。更多詳情敬請關注億速云行業資訊頻道。
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。