Python如何實現定積分與二重定積分的操作

這篇文章給大家分享的是有關Python如何實現定積分與二重定積分的操作的內容。小編覺得挺實用的，因此分享給大家做個參考，一起跟隨小編過來看看吧。

1.概述

最近項目需要使用程序實現數學微積分，最初想用java實現，后來發現可用文檔太少，實現比較麻煩，后來嘗試使用python實現，代碼量較少，主要有sympy與scipy兩種實現方式，本文主要記錄scipy的實現方式。

2.內容

2.1 所求函數

2.2 python代碼

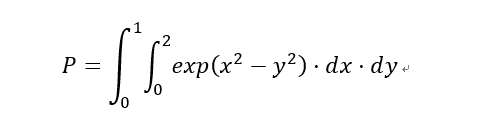
# 引入需要的包
import scipy.integrate
from numpy import exp
from math import sqrt
import math

# 創建表達式
f = lambda x,y : exp(x**2-y**2)

# 計算二重積分：（p:積分值，err:誤差）
# 這里注意積分區間的順序
# 第二重積分的區間參數要以函數的形式傳入
p,err= scipy.integrate.dblquad(f, 0, 2, lambda g : 0, lambda h : 1)	
print(p)

2.3 注意問題

1. exp盡量使用numpy的exp

2. 注意積分區間參數的順序

3. 第二重積分的區間參數要以函數的形式傳入

補充：python實現求解積分

例子 1：

假設有隨機變量 x，定義域 X，其概率密度函數為 p(x)，f(x) 為定義在 X 上的函數，目標是求函數 f(x) 關于密度函數 p(x) 的數學期望 。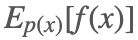

蒙特卡洛法根據概率分布 p(x) 獨立地抽樣 n 個樣本 x1,x2,…..xn，得到近似的 f(x) 期望為：

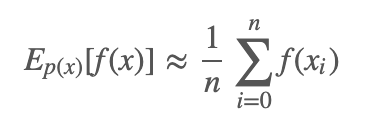
其實這個的理解就是要求一個擁有概率密度的函數期望值

期望=積分（每個點的密度函數*每個點的價值函數）

例子 2：

假設我們想要求解 h(x) 在 X 上的積分：

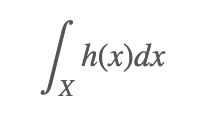
我們將 h(x) 分解成一個函數 f(x) 和一個概率密度函數 p(x) 的乘積，進而又將問題轉換為求解函數 f(x) 關于密度函數 p(x) 的數學期望 ：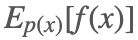

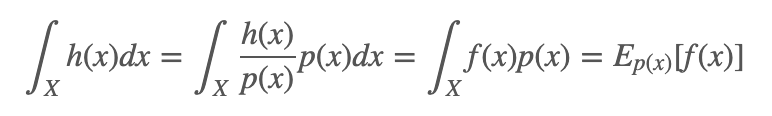
這里的Ep(x)是相當于把整個分布當時了概率分布，即總發生概率為1.

這里，f(x) 表示為 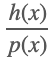，則有：

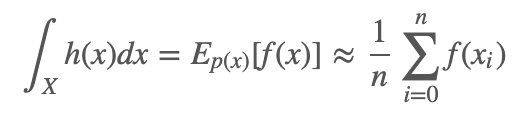
更一般的，假設我們想要求解 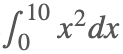，熟悉積分的同學肯定已經知道答案為 ，那么如何用采樣的方法來得到這個值呢？

令 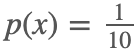，0<x<10，那么 。

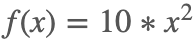下面是代碼：

'''import random
num=1000000
sum=0
for i in range(0,num):
    x=random.uniform(0,10)
    sum+=x*x*10
sum/=1000000
print(sum)'''
import random
numSamples=10000
samples=[random.uniform(0,10)for _ in range(numSamples)]
f_samples=[10*sample**2 for sample in samples]
result=1/10000.0*sum(f_samples)
print(result)

result=333.10527012455066

random.uniform(x,y)表示在[x,y)之間生成一個 實數

對于復雜的 h(x)，這種方法計算起來顯然就更加方便了（特別是忘記積分怎么算的同學）。

蒙特卡洛方法其實就是利用大數定理通過大量統計來算出最后的值。

到這里為止，我們簡單的介紹了蒙特卡洛方法，但是依舊沒有提到要怎么利用復雜的概率密度函數進行采樣。

接下來我們來看一下接受-拒絕法（accept-reject sampling method），它也是蒙特卡洛法中的一種類型適用于不能直接抽樣的情況。

感謝各位的閱讀！關于“Python如何實現定積分與二重定積分的操作”這篇文章就分享到這里了，希望以上內容可以對大家有一定的幫助，讓大家可以學到更多知識，如果覺得文章不錯，可以把它分享出去讓更多的人看到吧！