怎么在C語言中實現一個楊氏矩陣與楊輝三角

這篇文章將為大家詳細講解有關怎么在C語言中實現一個楊氏矩陣與楊輝三角，文章內容質量較高，因此小編分享給大家做個參考，希望大家閱讀完這篇文章后對相關知識有一定的了解。

C語言是什么

C語言是一門面向過程的、抽象化的通用程序設計語言，廣泛應用于底層開發，使用C語言可以以簡易的方式編譯、處理低級存儲器。

一、楊氏矩陣

楊氏矩陣

1.楊氏矩陣的概念

在數學中，楊表（英語：Young tableau），又稱楊氏矩陣。是對組合表示理論和舒伯特演算很有用的工具。它提供了一種方便的方式來描述對稱和一般線性群的群表示，并研究它們的性質。楊表是劍橋大學數學家 Alfred Young 在1900年推提出。然后，它被弗羅貝尼烏斯應用對稱群的研究中。他們的理論由許多數學家進一步發展，包括PercyMacMahon、W. V. D. Hodge、G. de B. Robinson、吉安-卡洛·羅塔、Alain Lascoux、Marcel-Paul Schützenberger 和 Richard P. Stanley 等。

2.楊氏矩陣的圖解

3.楊氏矩陣的實現

在一個 n * m 的二維數組中，每一行都按照從左到右遞增的順序排序，每一列都按照從上到下遞增的順序排序。請完成一個高效的函數，輸入這樣的一個二維數組和一個整數，判斷數組中是否含有該整數。

代碼如下：

bool findNumberIn2DArray(int** matrix, int matrixSize, int* matrixColSize, int target)
{
    if(matrixSize==0||*matrixColSize==0)
    {
        return false;
    }
    int row=0;
    int col=*matrixColSize-1;
    while(row<matrixSize&&col>=0)
    {
        if(matrix[row][col]>target)
        {
            col--;
        }
        else if(matrix[row][col]<target)
        {
            row++;
        }
        else if(matrix[row][col]==target)
        {
            return true;
        }
    }
    return false;
}

二、楊輝三角

楊輝三角

1.楊輝三角的概念

楊輝三角，是二項式系數在三角形中的一種幾何排列。在歐洲，這個表叫做帕斯卡三角形。帕斯卡（1623----1662）是在1654年發現這一規律的，比楊輝要遲393年，比賈憲遲600年。楊輝三角是中國古代數學的杰出研究成果之一，它把二項式系數圖形化，把組合數內在的一些代數性質直觀地從圖形中體現出來，是一種離散型的數與形的結合。

2.楊輝三角的圖解

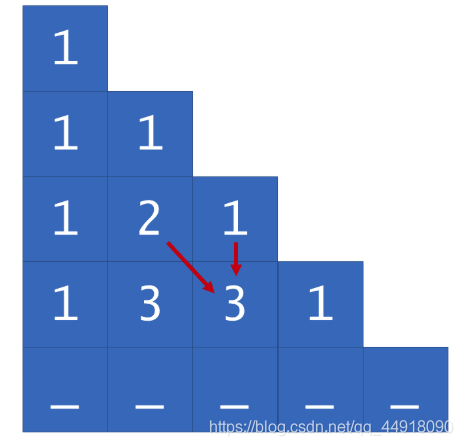
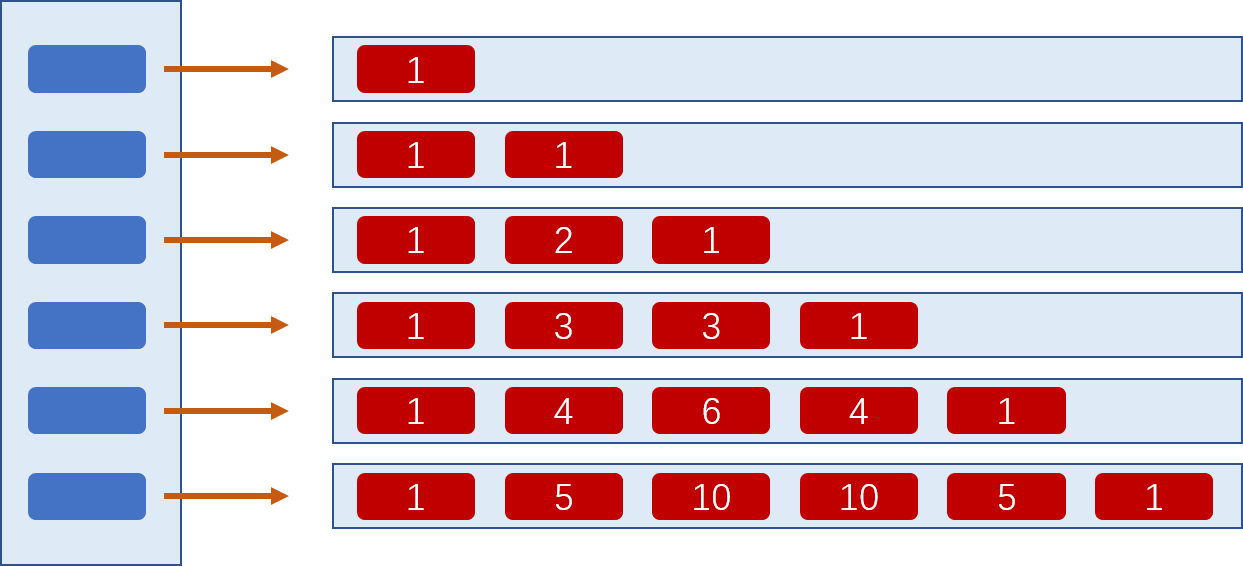
3.楊輝三角的實現

給定一個非負整數 numRows，生成楊輝三角的前 numRows 行。在楊輝三角中，每個數是它左上方和右上方的數的和。

代碼如下：

#define _CRT_SECURE_NO_WARNINGS   1
#include<stdio.h>
int** generate(int numRows, int* returnSize, int** returnColumnSizes)
{
	int row = 0;
	int col = 0;
	//ret是一個指針,它指向的是由指針構成的數組，指針指向對應的楊輝三角的一行數；ret也是二維數組
	int** ret = (int**)malloc(sizeof(int*)*numRows);
	//指定要返回的行數
	*returnSize = numRows;
	//分配每一列的具體空間
	*returnColumnSizes = malloc(sizeof(int)*numRows);
	for (row = 0; row < numRows; row++)
	{
		/* 分配楊輝三角中每一行的具體空間 */
		ret[row] = malloc(sizeof(int)* (row + 1));
		// 分配楊輝三角中每一行的列數
		(*returnColumnSizes)[row] = row + 1;
		ret[row][row] = ret[row][0] = 1;
		for (col = 1; col < row; col++)
		{
			ret[row][col] = ret[row - 1][col - 1] + ret[row - 1][col];
		}
	}
	return ret;
}
int main()
{
	return 0;
}

關于怎么在C語言中實現一個楊氏矩陣與楊輝三角就分享到這里了，希望以上內容可以對大家有一定的幫助，可以學到更多知識。如果覺得文章不錯，可以把它分享出去讓更多的人看到。