溫馨提示×
您好,登錄后才能下訂單哦!
點擊 登錄注冊 即表示同意《億速云用戶服務條款》
您好,登錄后才能下訂單哦!
這篇文章給大家分享的是有關python三邊測量定位怎么實現的內容。小編覺得挺實用的,因此分享給大家做個參考,一起跟隨小編過來看看吧。
1、云計算,典型應用OpenStack。2、WEB前端開發,眾多大型網站均為Python開發。3.人工智能應用,基于大數據分析和深度學習而發展出來的人工智能本質上已經無法離開python。4、系統運維工程項目,自動化運維的標配就是python+Django/flask。5、金融理財分析,量化交易,金融分析。6、大數據分析。
定位原理很簡單,故不贅述,直接上源碼,內附注釋。
#!/usr/bin/env python3
# -*- coding: utf-8 -*-
"""
Created on Wed May 16 10:50:29 2018
@author: dag
"""
import sympy
import numpy as np
import math
from matplotlib.pyplot import plot
from matplotlib.pyplot import show
import matplotlib.pyplot as plt
import matplotlib
#解決無法顯示中文問題,fname是加載字體路徑,根據自身pc實際確定,具體請百度
zhfont1 = matplotlib.font_manager.FontProperties(fname='/System/Library/Fonts/Hiragino Sans GB W3.ttc')
#隨機產生3個參考節點坐標
maxy = 1000
maxx = 1000
cx = maxx*np.random.rand(3)
cy = maxy*np.random.rand(3)
dot1 = plot(cx,cy,'k^')
#生成盲節點,以及其與參考節點歐式距離
mtx = maxx*np.random.rand()
mty = maxy*np.random.rand()
plt.hold('on')
dot2 = plot(mtx,mty,'go')
da = math.sqrt(np.square(mtx-cx[0])+np.square(mty-cy[0]))
db = math.sqrt(np.square(mtx-cx[1])+np.square(mty-cy[1]))
dc = math.sqrt(np.square(mtx-cx[2])+np.square(mty-cy[2]))
#計算定位坐標
def triposition(xa,ya,da,xb,yb,db,xc,yc,dc):
x,y = sympy.symbols('x y')
f1 = 2*x*(xa-xc)+np.square(xc)-np.square(xa)+2*y*(ya-yc)+np.square(yc)-np.square(ya)-(np.square(dc)-np.square(da))
f2 = 2*x*(xb-xc)+np.square(xc)-np.square(xb)+2*y*(yb-yc)+np.square(yc)-np.square(yb)-(np.square(dc)-np.square(db))
result = sympy.solve([f1,f2],[x,y])
locx,locy = result[x],result[y]
return [locx,locy]
#解算得到定位節點坐標
[locx,locy] = triposition(cx[0],cy[0],da,cx[1],cy[1],db,cx[2],cy[2],dc)
plt.hold('on')
dot3 = plot(locx,locy,'r*')
#顯示腳注
x = [[locx,cx[0]],[locx,cx[1]],[locx,cx[2]]]
y = [[locy,cy[0]],[locy,cy[1]],[locy,cy[2]]]
for i in range(len(x)):
plt.plot(x[i],y[i],linestyle = '--',color ='g' )
plt.title('三邊測量法的定位',fontproperties=zhfont1)
plt.legend(['參考節點','盲節點','定位節點'], loc='lower right',prop=zhfont1)
show()
derror = math.sqrt(np.square(locx-mtx) + np.square(locy-mty))
print(derror)輸出效果圖:
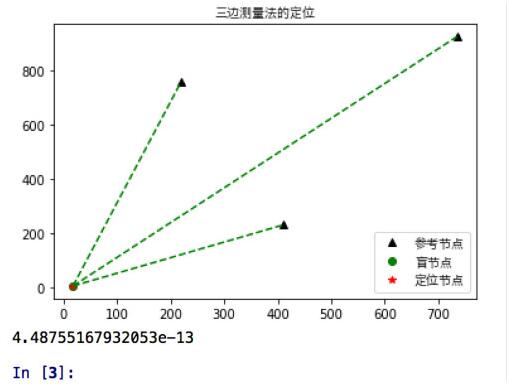
補充:python opencv實現三角測量(triangulation)
import cv2
import numpy as np
import scipy.io as scio
if __name__ == '__main__':
print("main function.")
#驗證點
point = np.array([1.0 ,2.0, 3.0])
#獲取相機參數
cams_data = scio.loadmat('/data1/dy/SuperSMPL/data/AMAfMvS_Dataset/cameras_I_crane.mat')
Pmats = cams_data['Pmats'] # Pmats(8, 3, 4) 投影矩陣
P1 = Pmats[0,::]
P3 = Pmats[2,::]
#通過投影矩陣將點從世界坐標投到像素坐標
pj1 = np.dot(P1, np.vstack([point.reshape(3,1),np.array([1])]))
pj3 = np.dot(P3, np.vstack([point.reshape(3,1),np.array([1])]))
point1 = pj1[:2,:]/pj1[2,:]#兩行一列,齊次坐標轉化
point3 = pj3[:2,:]/pj3[2,:]
#利用投影矩陣以及對應像素點,進行三角測量
points = cv2.triangulatePoints(P1,P3,point1,point3)
#齊次坐標轉化并輸出
print(points[0:3,:]/points[3,:])感謝各位的閱讀!關于“python三邊測量定位怎么實現”這篇文章就分享到這里了,希望以上內容可以對大家有一定的幫助,讓大家可以學到更多知識,如果覺得文章不錯,可以把它分享出去讓更多的人看到吧!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。