溫馨提示×
您好，登錄后才能下訂單哦！
點擊 登錄注冊 即表示同意《億速云用戶服務條款》
您好，登錄后才能下訂單哦！
PHP有關函數的編程思想(遞歸與迭代)
遞歸思想（遞歸函數）：
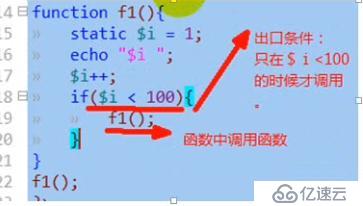
遞歸思想的一個基本形式是：在一個函數中，有至少一條語句，會去調用該函數自身。
但是從代碼角度來說，如果單純是函數內部調用函數，則會出現“出不來”的現象。
則我們就必須再來解決下一個問題：怎么終止（停止）這種自身的調用 -- 找到遞歸函數的出口
案例分析：寫一個遞歸函數，該函數可以計算一個正整數的階乘
數學基礎：
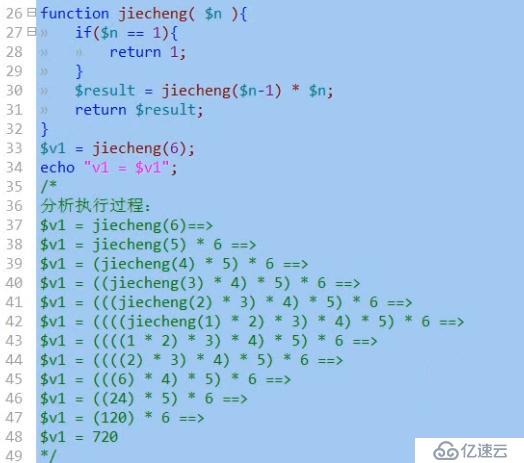
A：1的階乘是1
B：大于1的數的階乘是這個數減1的數的階乘，乘以該數的結果。
比如：要求6的階乘：則定義一個函數jiecheng() {......};該函數可以計算n的階乘
遞歸思想的總結：
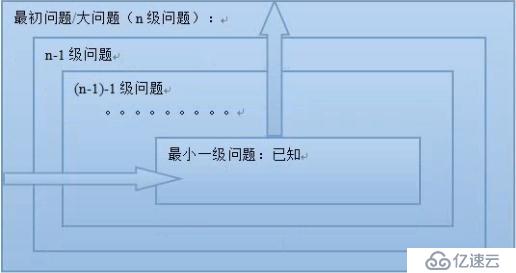
為了解決一個“大”問題，根據現實邏輯，該問題可以通過比它小一級的同類問題的答案而“輕松得到”。小一級的問題又可以通過更小一級的問題而輕松得到，依次類推 -- 直到“最小問題”，通常就是一個已知數（已知答案）。
遞歸思想的圖示：
迭代思想（遞推思想）：
遞推思想本身并不跟函數有直接關系（雖然常常寫在函數中）
其基本思路為：
為了解決一個“大”問題，根據現實邏輯，如果能夠找到同類問題的一個“最小問題”的答案（通常是已知的），并且根據已知算法，又可以因此得到比最小問題“大一級”問題的答案。而且，依次類推，又可以得到再大一級問題的答案。最終就可以得到“最大那個問題”（即要解決的問題）的答案。
可見，該思想的過程依賴于2個條件：
1：可知同類最小問題的答案
2：大一級問題的答案可以通過小一級問題的答案經過簡單運算規則而得到。
此思想的解題思路是：從小到大。對比遞歸思想是：從大到小，再回歸到大。
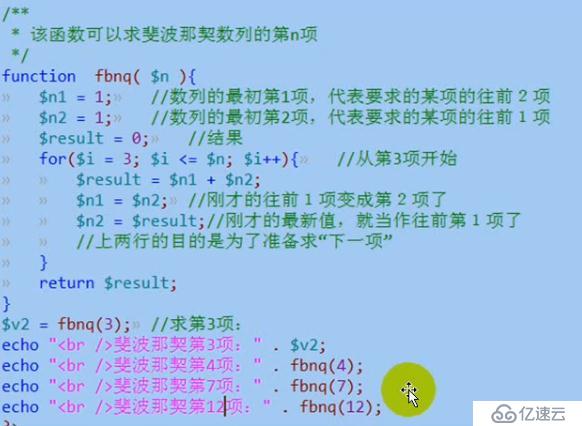
舉例：求斐波那契數列的第n項的值：
斐波那契數列（Fibonacci Sequence）的規則是：某項的值是其前兩項的值的和。前幾項的值為：1，1，2，3，5，8，13，21......(前兩項是已知的)
遞推算法的圖示：
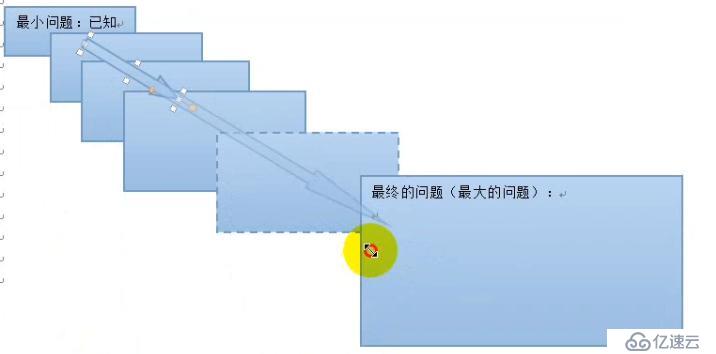
總結比較：
1：很多問題，用遞歸和遞推都可以解決。
2：有些問題只能用遞歸
3：如果兩種方法都可以解決，推薦使用遞推 -- 效率高很多！
免責聲明：本站發布的內容（圖片、視頻和文字）以原創、轉載和分享為主，文章觀點不代表本網站立場，如果涉及侵權請聯系站長郵箱：is@yisu.com進行舉報，并提供相關證據，一經查實，將立刻刪除涉嫌侵權內容。
