PHP如何實現迪科斯徹最短路徑算法

這篇文章給大家分享的是有關PHP如何實現迪科斯徹最短路徑算法的內容。小編覺得挺實用的，因此分享給大家做個參考，一起跟隨小編過來看看吧。

一、待解決問題

單源最短路徑問題，在給定有向圖中求一個頂點（單源頂點）到其他所有頂點的最短路徑問題。在下圖中，每條邊上有一個權值，希望求解A到所有其他頂點（B/C/D/E/F/G）的最短路徑。

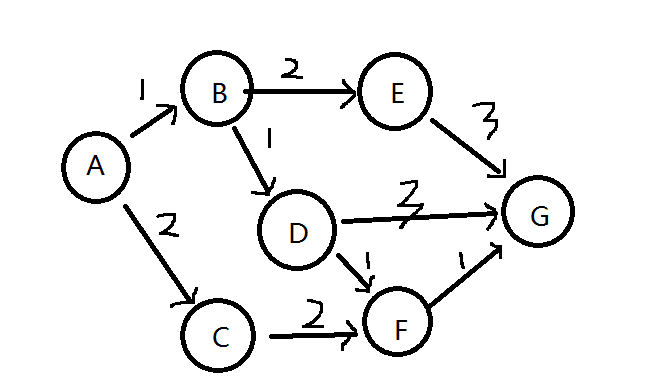
二、問題分析（最短路徑的子結構同樣最優性）

如果P（A,G）是從頂點A到G的最短路徑,假設D和F是這條路徑上的中間點，那么P(D,F)一定時從D到F的最短路徑。如果P(D,F)不是D到F的最短路徑，那必然存在某一個節點M的另一條D到F的路徑可以使P(A,B...M...F,G)比P(A,G)小，自相矛盾。

有了這樣的性質，我們可以了解Dijkstra算法。

三、Dijkstra算法

Dijkstra 算法，又叫迪科斯徹算法（Dijkstra），又稱為單源最短路徑算法，所謂單源是在一個有向圖中，從一個頂點出發，求該頂點至所有可到達頂點的最短路徑問題。 問題描述為設G=（V，E）是一個有向圖，V表示頂點，E表示邊。它的每一條邊（i，j）屬于E，都有一個非負權W（I,j），在G中指定一個結點v0，要求把從v0到G的每一個接vj（vj屬于V）的最短有向路徑找出來（或者指出不存在）。 Dijstra算法是運用貪心的策略，從源點開始，不斷地通過相聯通的點找出到其他點的最短距離。

Dijkstra的貪心應用在他利用（二）中的性質，不斷地選取“最近”的節點并試探每個節點的所有可能存在鏈接，以起始點為中心向外層層擴展，直到擴展到終點為止。對于源點A，逐步擴展，根據dist[j]=min{dist[j],dist[i]+matrix[i][j]}更新與i直接相鄰的頂點信息。

算法描述

1)算法思想：

設G=(V,E)是一個帶權有向圖，把圖中頂點集合V分成兩組，第一組為已求出最短路徑的頂點集合（用S表示，初始時S中只有一個源點，以后每求得一條最短路徑 , 就將加入到集合S中，直到全部頂點都加入到S中，算法就結束了），第二組為其余未確定最短路徑的頂點集合（用U表示），按最短路徑長度的遞增次序依次把第二組的頂點加入S中。在加入的過程中，總保持從源點v到S中各頂點的最短路徑長度不大于從源點v到U中任何頂點的最短路徑長度。此外，每個頂點對應一個距離，S中的頂點的距離就是從v到此頂點的最短路徑長度，U中的頂點的距離，是從v到此頂點只包括S中的頂點為中間頂點的當前最短路徑長度。

2)算法步驟：

a.初始時，S只包含源點，即S＝{v}，v的距離為0。U包含除v外的其他頂點，即:U={其余頂點}，若v與U中頂點u有邊，則<u,v>正常有權值，若u不是v的出邊鄰接點，則<u,v>權值為∞。

b.從U中選取一個距離v最小的頂點k，把k，加入S中（該選定的距離就是v到k的最短路徑長度）。

c.以k為新考慮的中間點，修改U中與k相鄰的各頂點的距離；若從源點v到頂點u的距離（經過頂點k）比原來距離（不經過頂點k）短，則修改頂點u的距離值，修改后的距離值為頂點k的距離加上k與u邊上的權。

d.重復步驟b和c直到所有頂點都包含在S中。

四、算法PHP實現

<?php
class Dijkstra
{
  private $G;
  public function __construct()
  {
    //有向圖存儲
    $this->G = array(
      array(0,1,2,0,0,0,0),
      array(0,0,0,1,2,0,0),
      array(0,0,0,0,0,2,0),
      array(0,0,0,0,0,1,3),
      array(0,0,0,0,0,0,3),
      array(0,0,0,0,0,0,1),
      array(0,0,0,0,0,0,0),
    );
  }
  public function calculate()
  {
    // 存儲已經選擇節點和剩余節點
    $U = array(0);
    $V = array(1,2,3,4,5,6);
    // 存儲路徑上節點距離源點的最小距離
    $d = array();
    //初始化圖中節點與源點0的最小距離
    for($i=1;$i<7;$i++)
    {
      if($this->G[0][$i]>0)
      {
        $d[$i] = $this->G[0][$i];
      }
      else
      {
        $d[$i] = 1000000;
      }
    }
    // n-1次循環完成轉移節點任務
    for($l=0;$l<6;$l++)
    {
      // 查找剩余節點中距離源點最近的節點v
      $current_min = 100000;
      $current_min_v = 0;
      foreach($V as $k=>$v)
      {
        if($d[$v] < $current_min)
        {
          $current_min = $d[$v];
          $current_min_v = $v;
        }
      }
      //從V中更新頂點到U中
      array_push($U,$current_min_v);
      array_splice($V,array_search($current_min_v,$V),1);
      //更新
      foreach($V as $k=>$u)
      {
        if($this->G[$current_min_v][$u]!=0&&$d[$u]>$d[$current_min_v]+$this->G[$current_min_v][$u])
        {
          $d[$u] = $d[$current_min_v]+$this->G[$current_min_v][$u];
        }
      }
    }
    foreach($d as $k => $u)
    {
      echo $k.'=>'.$u.'<br>';
    }
  }
}
?>

調用類：

$D = new Dijkstra;
$D->calculate();

執行結果：

1=>1
2=>2
3=>2
4=>3
5=>3
6=>4

感謝各位的閱讀！關于“PHP如何實現迪科斯徹最短路徑算法”這篇文章就分享到這里了，希望以上內容可以對大家有一定的幫助，讓大家可以學到更多知識，如果覺得文章不錯，可以把它分享出去讓更多的人看到吧！