您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
PHP中有哪些常用的排序算法?很多新手對此不是很清楚,為了幫助大家解決這個難題,下面小編將為大家詳細講解,有這方面需求的人可以來學習下,希望你能有所收獲。
1 快速排序
快速排序是由東尼·霍爾發展的一種排序算法。
在平均狀況下,排序 n 個項目要Ο(n log n)次比較。
在最壞狀況下則需要Ο(n2)次比較,但這種狀況并不常見。
事實上,快速排序通常明顯比其他Ο(n log n) 算法更快,因為它的內部循環可以在大部分的架構上,很有效率地被實現出來。
快速排序采用分治法實現排序,具體步驟:
從數列中挑出一個數作為基準元素。通常選擇第一個或最后一個元素。
掃描數列,以基準元素為比較對象,把數列分成兩個區。規則是:小的移動到基準元素前面,大的移到后面,相等的前后都可以。分區完成之后,基準元素就處于數列的中間位置。
然后再用同樣的方法,遞歸地排序劃分的兩部分。
遞歸的結束條件是數列的大小是0或1,也就是永遠都已經被排序好了。
PHP代碼實現:
function quickSort($arr)
{
$len = count($arr);
// 先設定結束條件,判斷是否需要繼續進行
if($len <= 1) {
return $arr;
}
// 選擇第一個元素作為基準元素
$pivot = $arr[0];
// 初始化左數組
$left = $right = array();
// 初始化大于基準元素的右數組
$right = array();
// 遍歷除基準元素外的所有元素,按照大小關系放入左右數組內
for ($i = 1; $i < $len ; $i++) {
if ($arr[$i] < $pivot) {
$left[] = $arr[$i];
} else {
$right[] = $arr[$i];
}
}
// 再分別對左右數組進行相同的排序
$left = quickSort($left);
$right = quickSort($right);
// 合并基準元素和左右數組
return array_merge($left, array($pivot), $right);
}原地排序版本,不需要額外的存儲空間:
function partition(&$arr, $leftIndex, $rightIndex)
{
$pivot = $arr[($leftIndex + $rightIndex) / 2];
while ($leftIndex <= $rightIndex) {
while ($arr[$leftIndex] < $pivot) {
$leftIndex++;
}
while ($arr[$rightIndex] > $pivot) {
$rightIndex--;
}
if ($leftIndex <= $rightIndex) {
list($arr[$leftIndex], $arr[$rightIndex]) = [$arr[$rightIndex], $arr[$leftIndex]];
$leftIndex++;
$rightIndex--;
}
}
return $leftIndex;
}
function quickSort(&$arr, $leftIndex, $rightIndex)
{
if ($leftIndex < $rightIndex) {
$index = partition($arr, $leftIndex, $rightIndex);
quickSort($arr, $leftIndex, $index - 1);
quickSort($arr, $index, $rightIndex);
}
}2 冒泡排序
冒泡排序是一種簡單的排序算法。
算法重復地走訪過要排序的數列,一次比較兩個元素,如果他們的順序錯誤就把他們交換過來。
走訪數列的工作重復地進行,直到沒有再需要交換,也就是說該數列已經排序完成。
因為排序過程讓較大的數往下沉,較小的往上冒,故而叫冒泡法。

算法步驟:
從第一個元素開始,比較相鄰的元素,如果第一個比第二個大,就交換他們兩個。
從開始第一對到結尾的最后一對,對每一對相鄰元素作同樣的工作。比較結束后,最后的元素應該會是最大的數。
對所有的元素重復以上的步驟,除了最后一個。
重復上面的步驟,每次比較的對數會越來越少,直到沒有任何一對數字需要比較。
PHP代碼實現:
function bubbleSort($arr)
{
$len = count($arr);
for($i = 1; $i < $len; $i++) {
for($k = 0; $k < $len - $i; $k++) {
if($arr[$k] > $arr[$k + 1]) {
$tmp = $arr[$k + 1];
$arr[$k + 1] = $arr[$k];
$arr[$k] = $tmp;
}
}
}
return $arr;
}3 插入排序
插入排序是一種簡單直觀的排序算法。
插入排序的工作原理是:將需要排序的數,與前面已經排好序的數據從后往前進行比較,使其插入到相應的位置。
插入排序在實現上,通常采用in-place排序,即只需用到O(1)的額外空間的排序。
因而,在從后向前掃描過程中,需要反復把已排序元素逐步向后挪位,為最新元素提供插入空間。
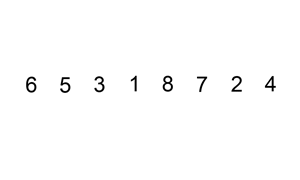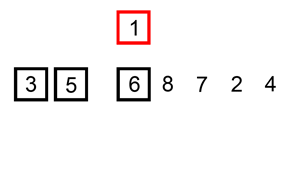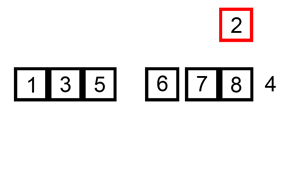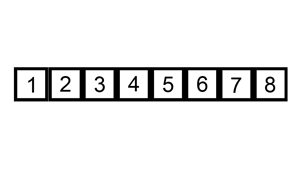
算法步驟:
從第一個元素開始,該元素可以認為已經被排序;
取出下一個元素,在已經排序的元素序列中從后向前掃描;
如果以排序的元素大于新元素,將該元素移到下一位置;
重復步驟3,直到找到已排序的元素小于或者等于新元素的位置;
將新元素插入到該位置中;
重復步驟2。
PHP代碼實現:
function insertSort($arr)
{
$len = count($arr);
for ($i = 1; $i < $len; $i++) {
$tmp = $arr[$i];
for ($j = $i - 1; $j >= 0; $j--) {
if ($tmp < $arr[$j]) {
$arr[$j + 1] = $arr[$j];
$arr[$j] = $tmp;
} else {
break;
}
}
}
return $arr;
}4 選擇排序
選擇排序是一種簡單直觀的排序算法。

算法步驟:
首先,在序列中找到最小元素,存放到排序序列的起始位置;
接著,從剩余未排序元素中繼續尋找最小元素,放到已排序序列的末尾。
重復第二步,直到所有元素均排序完畢。
PHP代碼實現:
function selectSort($arr)
{
$len = count($arr);
for ($i = 0; $i < $len; $i++) {
$p = $i;
for ($j = $i + 1; $j < $len; $j++) {
if ($arr[$p] > $arr[$j]) {
$p = $j;
}
}
$tmp = $arr[$p];
$arr[$p] = $arr[$i];
$arr[$i] = $tmp;
}
return $arr;
}5 歸并排序
歸并排序是建立在歸并操作上的一種有效的排序算法。
歸并排序將待排序的序列分成若干組,保證每組都有序,然后再進行合并排序,最終使整個序列有序。
該算法是采用分治法的一個非常典型的應用。
算法步驟:
申請空間,使其大小為兩個已經排序序列之和,該空間用來存放合并后的序列;
設定兩個指針,最初位置分別為兩個已經排序序列的起始位置
比較兩個指針所指向的元素,選擇相對小的元素放入到合并空間,并移動指針到下一位置
重復步驟3直到某一指針達到序列尾
將另一序列剩下的所有元素直接復制到合并序列尾
排序效果:

PHP實現代碼:
/**
* 歸并排序
*
* @param array $lists
* @return array
*/
function merge_sort(array $lists)
{
$n = count($lists);
if ($n <= 1) {
return $lists;
}
$left = merge_sort(array_slice($lists, 0, floor($n / 2)));
$right = merge_sort(array_slice($lists, floor($n / 2)));
$lists = merge($left, $right);
return $lists;
}
function merge(array $left, array $right)
{
$lists = [];
$i = $j = 0;
while ($i < count($left) && $j < count($right)) {
if ($left[$i] < $right[$j]) {
$lists[] = $left[$i];
$i++;
} else {
$lists[] = $right[$j];
$j++;
}
}
$lists = array_merge($lists, array_slice($left, $i));
$lists = array_merge($lists, array_slice($right, $j));
return $lists;
}6 堆排序
堆排序是指利用堆這種數據結構所設計的一種排序算法。
堆積是一個近似完全二叉樹的結構,并同時滿足堆積的性質:即子結點的鍵值或索引總是小于(或者大于)它的父節點。
堆排序的平均時間復雜度為Ο(nlogn) 。
算法步驟:
創建一個堆H[0..n-1];
把堆首(最大值)和堆尾互換;
把堆的尺寸縮小1,并調用shift_down(0),目的是把新的數組頂端數據調整到相應位置;
重復步驟2,直到堆的尺寸為1。
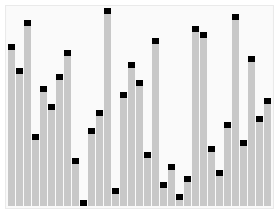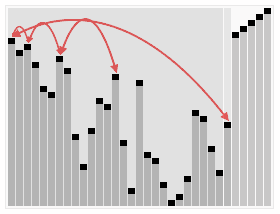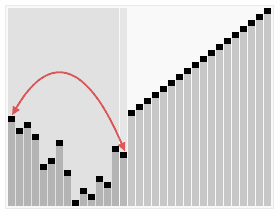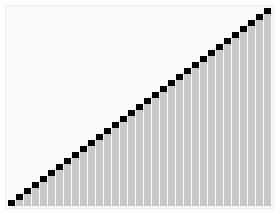
PHP實現代碼:
/**
* 堆排序
*
* @param array $lists
* @return array
*/
function heap_sort(array $lists)
{
$n = count($lists);
build_heap($lists);
while (--$n) {
$val = $lists[0];
$lists[0] = $lists[$n];
$lists[$n] = $val;
heap_adjust($lists, 0, $n);
//echo "sort: " . $n . "\t" . implode(', ', $lists) . PHP_EOL;
}
return $lists;
}
function build_heap(array &$lists)
{
$n = count($lists) - 1;
for ($i = floor(($n - 1) / 2); $i >= 0; $i--) {
heap_adjust($lists, $i, $n + 1);
//echo "build: " . $i . "\t" . implode(', ', $lists) . PHP_EOL;
}
//echo "build ok: " . implode(', ', $lists) . PHP_EOL;
}
function heap_adjust(array &$lists, $i, $num)
{
if ($i > $num / 2) {
return;
}
$key = $i;
$leftChild = $i * 2 + 1;
$rightChild = $i * 2 + 2;
if ($leftChild < $num && $lists[$leftChild] > $lists[$key]) {
$key = $leftChild;
}
if ($rightChild < $num && $lists[$rightChild] > $lists[$key]) {
$key = $rightChild;
}
if ($key != $i) {
$val = $lists[$i];
$lists[$i] = $lists[$key];
$lists[$key] = $val;
heap_adjust($lists, $key, $num);
}
}7 希爾排序
希爾排序,也稱遞減增量排序算法,是插入排序的一種更高效的改進版本。
但希爾排序是非穩定排序算法。
希爾排序是基于插入排序的以下兩點性質而提出改進方法的:
插入排序在對幾乎已經排好序的數據操作時, 效率高, 即可以達到線性排序的效率
但插入排序一般來說是低效的, 因為插入排序每次只能將數據移動一位
算法步驟:
先將整個待排序的記錄序列分割成為若干子序列,分別進行直接插入排序
待整個序列中的記錄“基本有序”時,再對全體記錄進行依次直接插入排序。
PHP實現代碼:
/**
* 希爾排序 標準
*
* @param array $lists
* @return array
*/
function shell_sort(array $lists)
{
$n = count($lists);
$step = 2;
$gap = intval($n / $step);
while ($gap > 0) {
for ($gi = 0; $gi < $gap; $gi++) {
for ($i = $gi; $i < $n; $i += $gap) {
$key = $lists[$i];
for ($j = $i - $gap; $j >= 0 && $lists[$j] > $key; $j -= $gap) {
$lists[$j + $gap] = $lists[$j];
$lists[$j] = $key;
}
}
}
$gap = intval($gap / $step);
}
return $lists;
}8 基數排序
基數排序是一種非比較型整數排序算法,其原理是將整數按位數切割成不同的數字,然后按每個位數分別比較。
由于整數也可以表達字符串(比如名字或日期)和特定格式的浮點數,所以基數排序也不是只能使用于整數。

說基數排序之前,我們簡單介紹桶排序:
桶排序是將陣列分到有限數量的桶子里。
每個桶子再個別排序,有可能再使用別的排序算法,或是以遞回方式繼續使用桶排序進行排序。
桶排序是鴿巢排序的一種歸納結果。
當要被排序的陣列內的數值是均勻分配的時候,桶排序使用線性時間O(n)。
但桶排序并不是 比較排序,他不受到 O(n log n) 下限的影響。
簡單來說,就是把數據分組,放在一個個的桶中,然后對每個桶里面的在進行排序。
例如,要對大小為[1..1000]范圍內的n個整數A[1..n]排序
首先,可以把桶設為大小為10的范圍,具體而言,設集合B[1]存儲[1..10]的整數,集合B[2]存儲 (10..20]的整數,……集合B[i]存儲( (i-1)*10, i*10]的整數,i = 1,2,..100。總共有 100個桶。
然后,對A[1..n]從頭到尾掃描一遍,把每個A[i]放入對應的桶B[j]中。 再對這100個桶中每個桶里的數字排序,這時可用冒泡,選擇,乃至快排,一般來說任 何排序法都可以。
最后,依次輸出每個桶里面的數字,且每個桶中的數字從小到大輸出,這 樣就得到所有數字排好序的一個序列了。
假設有n個數字,有m個桶,如果數字是平均分布的,則每個桶里面平均有n/m個數字。
如果對每個桶中的數字采用快速排序,那么整個算法的復雜度是
O(n + m * n/m*log(n/m)) = O(n + nlogn – nlogm)
從上式看出,當m接近n的時候,桶排序復雜度接近O(n)
當然,以上復雜度的計算是基于輸入的n個數字是平均分布這個假設的。這個假設是很強的 ,實際應用中效果并沒有這么好。如果所有的數字都落在同一個桶中,那就退化成一般的排序了。
前面說的幾大排序算法 ,大部分時間復雜度都是O(n2),也有部分排序算法時間復雜度是O(nlogn)。而桶式排序卻能實現O(n)的時間復雜度。但桶排序的缺點是:
1)首先是空間復雜度比較高,需要的額外開銷大。排序有兩個數組的空間開銷,一個存放待排序數組,一個就是所謂的桶,比如待排序值是從0到m-1,那就需要m個桶,這個桶數組就要至少m個空間。
2)其次待排序的元素都要在一定的范圍內等等。
/**
* 基數排序
*
* @param array $lists
* @return array
*/
function radix_sort(array $lists)
{
$radix = 10;
$max = max($lists);
$k = ceil(log($max, $radix));
if ($max == pow($radix, $k)) {
$k++;
}
for ($i = 1; $i <= $k; $i++) {
$newLists = array_fill(0, $radix, []);
for ($j = 0; $j < count($lists); $j++) {
$key = $lists[$j] / pow($radix, $i - 1) % $radix;
$newLists[$key][] = $lists[$j];
}
$lists = [];
for ($j = 0; $j < $radix; $j++) {
$lists = array_merge($lists, $newLists[$j]);
}
}
return $lists;
}9 總結
各種排序的穩定性,時間復雜度、空間復雜度、穩定性總結如下圖:
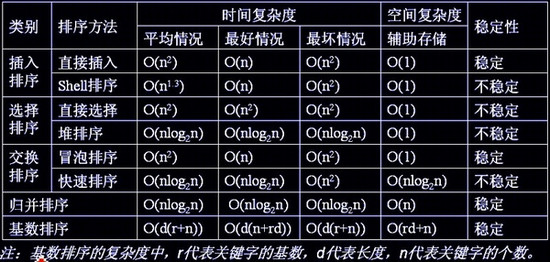
關于時間復雜度:
(1)平方階(O(n2))排序
各類簡單排序:直接插入、直接選擇和冒泡排序;
(2)線性對數階(O(nlog2n))排序
快速排序、堆排序和歸并排序;
(3)O(n1+§))排序,§是介于0和1之間的常數。
希爾排序
(4)線性階(O(n))排序
基數排序,此外還有桶、箱排序。
關于穩定性:
穩定的排序算法:冒泡排序、插入排序、歸并排序和基數排序
不是穩定的排序算法:選擇排序、快速排序、希爾排序、堆排序
看完上述內容是否對您有幫助呢?如果還想對相關知識有進一步的了解或閱讀更多相關文章,請關注億速云行業資訊頻道,感謝您對億速云的支持。
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。