您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
小編這次要給大家分享的是C++如何實現求等差素數列,文章內容豐富,感興趣的小伙伴可以來了解一下,希望大家閱讀完這篇文章之后能夠有所收獲。
題目
標題:等差素數列
2,3,5,7,11,13,....是素數序列。
類似:7,37,67,97,127,157 這樣完全由素數組成的等差數列,叫等差素數數列。
上邊的數列公差為30,長度為6。
2004年,格林與華人陶哲軒合作證明了:存在任意長度的素數等差數列。
這是數論領域一項驚人的成果!
有這一理論為基礎,請你借助手中的計算機,滿懷信心地搜索:
長度為10的等差素數列,其公差最小值是多少?
注意:需要提交的是一個整數,不要填寫任何多余的內容和說明文字。
題解
絮絮叨叨(罵罵咧咧
一開始看到這道題還是有點懵的,畢竟我個數學小白,對素數什么的最發怵了。
然后找了好多大佬的題解都沒看明白,甚至有一個大佬的代碼看的我暈頭轉向~
然后終于被我找到一份能看懂并且覺得非常正確的代碼,思路如下:
思路
兩層循環,一層循環用于循環公差,一層循環用于循環起始素數。
需要注意的是,內層循環起始素數的時候,不能無邊界循環下去,要設置一個上限,否則外層循環永遠無法走到下一個公差(自己寫的時候自以為是犯的錯
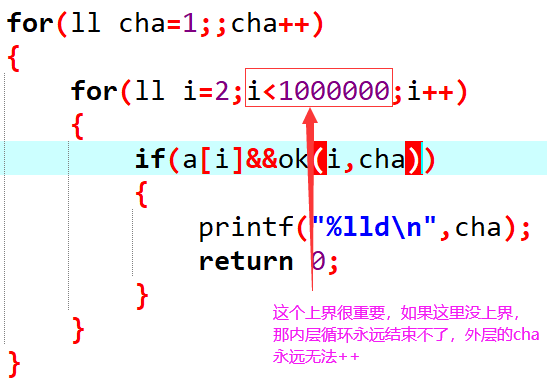
內層循環走的時候,只需要判斷:
①這個數是不是素數(作為起始素數最基本的條件)
②判斷從這個素數開始,以cha為公差能否存在連續10個等差的素數。【用ok函數來判斷的】
如果以上兩個條件都滿足,則這就是我們要找的長度為10的等差素數列,其公差的最小值
因為我們是從小到大找的,那我們找到的滿足條件的第一個就是答案~
#include<stdio.h>
#include<string.h>
#include<math.h>
#include<algorithm>
using namespace std;
typedef long long ll;
const ll maxn=1e6+50;
ll a[maxn];
bool ok(ll n,ll cha)
{
for(ll i=0;i<10;i++)
{
if(!a[n+i*cha])return 0;
}
return 1;
}
int main()
{
a[1]=0;
a[2]=1;
a[3]=1;
for(ll i=4;i<=1000000;i++)
{
bool flag=0;
for(ll j=2;j*j<=i;j++)
{
if(i%j==0)
{
flag=1;
break;
}
}
if(flag)a[i]=0;
else a[i]=1;
}
for(ll cha=1;;cha++)
{
for(ll i=2;i<1000000;i++)
{
if(a[i]&&ok(i,cha))
{
printf("%lld\n",cha);
return 0;
}
}
}
}看完這篇關于C++如何實現求等差素數列的文章,如果覺得文章內容寫得不錯的話,可以把它分享出去給更多人看到。
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。