Python實戰教程：拒絕調包，如何用python推導線性回歸模型

最近有人問我一個問題，我數學不好，代碼基礎薄弱，英語一般般，如何入門當今最為前沿的機器學習領域？均方差損失，MSE，平方損失函數，二次代價函數都是什么意思？

這個問題問得好，諸如學好數學，多敲代碼，攻克專八這類標準回答我就不多說了。我們這回用 Python實戰教程案例，分分鐘帶你入門。

下面我們通過機器學習的入門模型——線性回歸，從數學說起，以代碼著手，一步步推導出可以應用于實踐的模型。

線性回歸的數學原理

首先，先看一張圖：

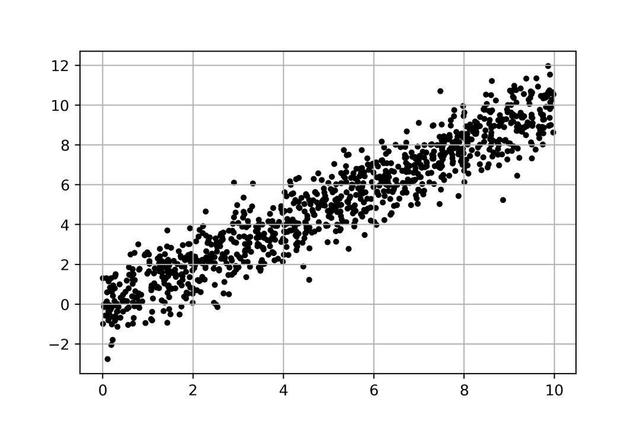
圖是我們在初中學習過的直角坐標系二維平面，上面遍布著一些點。從整體趨勢看，y隨x的增大而增大。如果曾經你和我一樣，數學每次考試都是90的話，那么接下來，我相信你會情不自禁地做一件事：

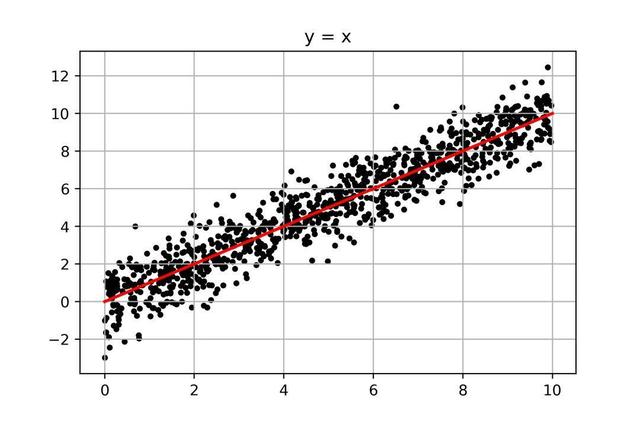
沒錯，我們會以（0,0）和（10,10）為兩點，畫出一條貫穿其中的線，從視覺上，這條紅線正好把所有點一分為二，其對應的數學表達式為：

y=x

而這就是我們線性回歸所要做的事：找到一組數學表達式（圖中的紅線），用來反映數據（圖中的點）的變化規律。

目標有了，問題也來了：

貫穿圖中密密麻麻點的線有無數條，為什么不是y=2x，y=x+1，偏偏是y=x呢？

我們又是通過何種方法去找到這條線呢？

先解決第一個問題，上天書：

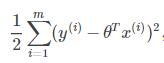
這個式子就是第一個問題的解，沒見過的符號太多，看不懂是吧？那么我來翻譯一下：

1. 先求出（每個點的Y值-以每個點的X值通過函數求出的Y值）的平方
2. 求和；
3. 乘以1/2

再通俗點：

把每個點的實際y值與它通過某個函數求出的y值的差的平方加起來，再乘以1/2。

而文章開篇中的均方差損失，MSE，平方損失函數，二次代價函數其實都指的是它。這個式子其實計算的是真實值和用函數預測的值之間的誤差之和。那么第一個問題就迎刃而解了：哪一個表達式所求出的誤差和最小，就是我們要找的那條“紅線”。

我們繼續解決第二個問題，先上圖：

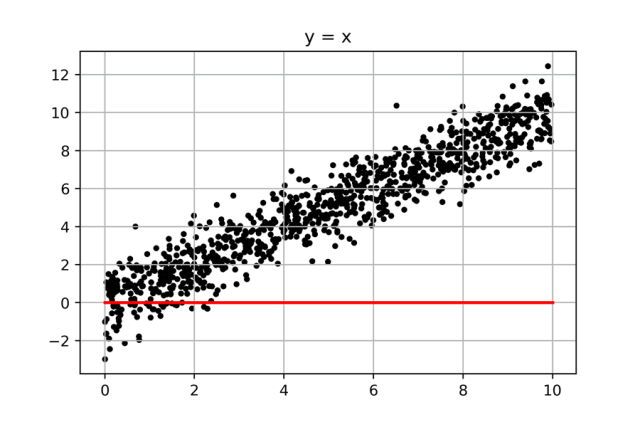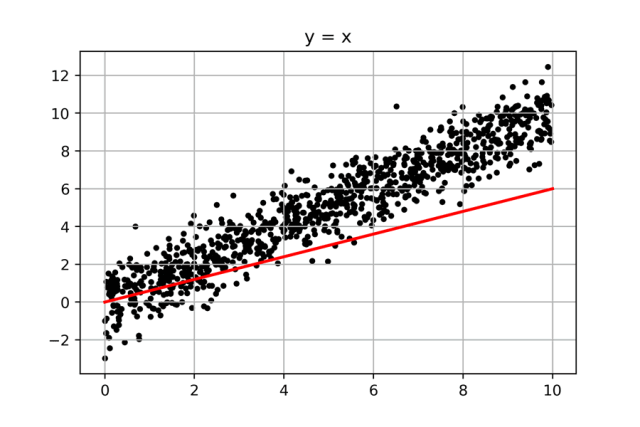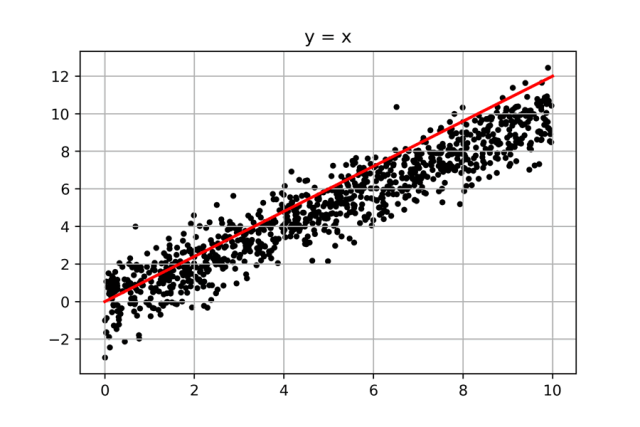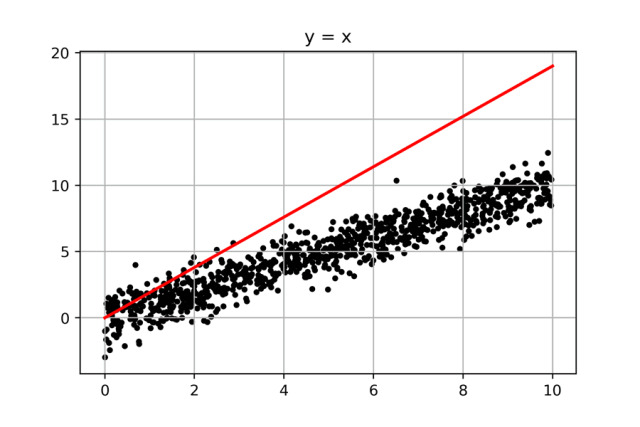
這個問題還要簡單，我們只要從斜率為0的那條“紅線”（y=0*X）開始畫線，然后一點點增大斜率，每條線求一個誤差值，找出其中誤差值最小的那條線，就大功告成了。而中間有著巨大計算量的遍歷過程，我們可以通過python，瞬間完成。

線性回歸的Python實現

重點：梯度下降法！

導入一些包，待用：

import numpy as npimport pandas as pdfrom sklearn.linear_model import LinearRegressionfrom sklearn.preprocessing import MinMaxScalerimport matplotlib.pyplot as pltimport seaborn as snssns.set_context('notebook')sns.set_style('white')

導入案例數據：

model_data = pd.read_csv('model_data.csv',engine='python')model_data.head()

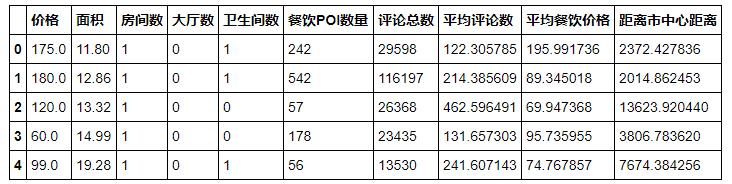
數據是一份上海的房價數據，我們要把房屋價格作為因變量y,房屋面積，房間數附近餐飲POI數量，評論，距離市中心距離等作為自變量，擬合一個線性回歸模型，用于預測房價。

根據要求提取自變量和因變量：

feat_cols = model_data.columns.tolist()[1:]print(feat_cols)

X = model_data[feat_cols].valuesy = model_data['價格'].values

構建損失函數：

def Cost_Function(X,y,theta): ''' 需要傳入的參數為 X：自變量 y:應變量 theta:權重 使用均方誤差（MSE），作為損失函數 ''' m = y.size #求出y的個數（一共多少條數據） t = X.dot(theta) #權重和變量點乘，計算出使用當前權重時的預測值 c = 0 #定義損失值 c = 1/(2*m) * (np.sum(np.square(t-y))) #預測值與實際值的差值，平方后除以數據的條數，計算出均方誤差。最后乘以1/2（無實際意義，方便以后計算） return c #返回損失值

*θ為每個變量前的權重，什么是權重？比如y=2x,2就是自變量x的權重

求損失值我們就用先前說到的損失函數。如果你夠仔細，可能會有一個問題，我們的損失函數前需要乘以一個1/2，似乎沒有特別的意義。恭喜你很機智，1/2的確沒有任何意義，只是為了接下來方便求導。

構建梯度下降法：

def GradientDescent(X, y, feat_cols, alpha=0.3, num_iters=10000): ''' 需傳入參數為 X：自變量 y:應變量 feat_cols：變量列表 alpha：學習率，默認0.3 num_iters：迭代次數，默認10000次 使用梯度下降法迭代權重 ''' scaler = MinMaxScaler() #最大最小值歸一化自變量 X = scaler.fit_transform(X) #歸一化 m = y.size #求出y的個數（一共多少條數據） J_history = np.zeros(num_iters) #創建容納每次迭代后損失值得矩陣，初始值為0 theta = np.zeros(len(feat_cols)+1) #設置默認權重，0 for iter in np.arange(num_iters): #根據迭代次數，開始迭代 t = X.dot(theta) #權重和變量點乘，計算出使用當前權重時的預測值 theta = theta - alpha*(1/m)*(X.T.dot(t-y)) #對代價函數求導，算出下降最快的方向，乘以學習率（下降的速度），再用原來的權重相減，得到新的權重 J_history[iter] = Cost_Function(X, y, theta) #求出新的權重時的損失值，存入矩陣 return(theta, J_history) #返回最終的權重和歷次迭代的損失值

這是構造模型最為核心的部分。我們不斷迭代，尋找最優的那條“紅線”的過程，其實是在不斷調整每個自變量的權重。而每個權重每次到底怎么調整，增大還是減小（方向），這就需要我們對損失函數求導。

如果數學不好，不理解，我們用圖來說明一下：

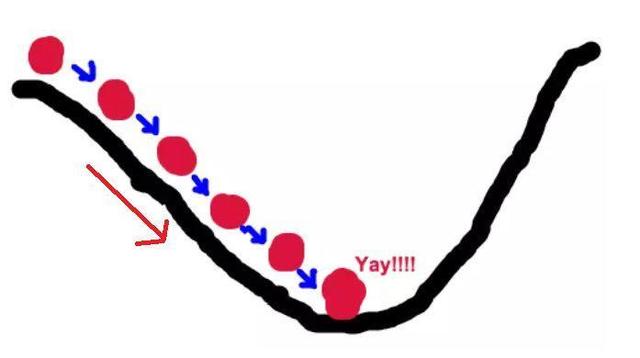
好比，我們站在懸崖頂端，要找到最快能達到懸崖底部的方向，那么顯而易見，你所在位置最陡峭的方向，就是正確的方向，而求導就是找到最陡峭的方向（切線斜率絕對值最大的點）。

山坡是凹凸不平的，所以我們每走一步都需要重新尋找方向，這就是迭代的過程；其次，每次的步子也不能跨太大，萬一跨錯地方了，不好糾正，所以我們又需要設置一個步子的大小——學習率。

所以梯度下降法的公式就是：

每一次更新的權重= 前一次的權重-學習率X損失函數的導數。

在理解了下山這個場景以后，我們就能順利的完成梯度下降法的構建，并且通過python函數求出最后每個變量的權重和每次迭代過后的損失值。

構建繪制損失值變化圖的函數：

def plot_Cost(GD_result): ''' 繪制權重變化情況 需傳入參數為 GD_result：梯度下降法結果 ''' theta , Cost = GD_result #得到權重和損失值 print('theta: ',theta.ravel()) #打印權重 plt.plot(Cost) #繪制損失值變化情況 plt.title('COST change') plt.ylabel('Cost') plt.xlabel('Iterations') plt.grid() plt.show()

這個很簡單，就是通過前面梯度下降法求得的歷次迭代后的損失值，畫出變化曲線。

最后把所有函數匯總，就是我們的線性回歸模型了：

def lr_function(X,y,feat_cols): ''' 需要輸入的變量為 X：自變量 y:應變量 feat_cols：變量列表 ''' def score(y_p,y): ''' y_p:預測值 y:真實值 dimension：樣本數量 計算R^和調整R^ ''' aa=y_p.copy(); bb=y.copy() if len(aa)!=len(bb): print('not same length') return np.nan cc=aa-bb wcpfh=sum(cc**2) #誤差平方和 # RR means R_Square RR=1-sum((bb-aa)**2)/sum((bb-np.mean(bb))**2) return RR#返回R^ X = np.c_[np.ones(X.shape[0]),X] GD_result = GradientDescent(X, y, feat_cols) plot_Cost(GD_result) y_p = np.dot(X,GD_result[0]) RR = score(y_p,y) return RR,y_p,GD_result[0] #返回R^,預測值

一般對于每個機器學習模型，都需要有一個指標衡量其擬合程度，而線性模型我們使用的是我們所熟知的**可決系數R2**。為了求出R2，

我在函數中又套用了一個簡單的求解函數，具體過程不贅述了，通讀代碼就能明白。通常R^2越接近1，表示模型擬合程度越好。

模型封裝完畢，下面是見證奇跡的時刻！

model_result = lr_function(X,y,feat_cols)print('R^2為:{}'.format(round(model_result[0],4)))

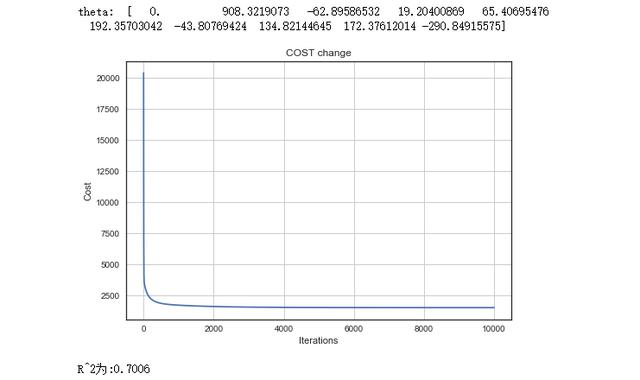
通過模型，我們求出了每個自變量的權重，圖表反應了損失值由大變小的過程，在10000次迭代的過程中，一開始速度很快，越到后面越趨于平緩。

最后是R^2為0.70，有70%的擬合度，尚可。

線性回歸模型的驗證

為了驗證我們自己編寫的模型是否準確，我們也可以使用python機器學習工具包sklearn，對同樣的數據，用線性回歸模型擬合，查看最后的R^2是否一致。

先對變量標準化：

scaler = MinMaxScaler()X = scaler.fit_transform(X)

使用LinearRegression()進行擬合，并求出R^2：

lr = LinearRegression()lr.fit(X,y)R2 = lr.score(X,y)print('R^2為:{}'.format(round(R2,4)))

R^2同樣為0.7，代表我們自己編寫的模型沒有問題。

最后，我們繪制一張真實值與預測值對比圖，可視化模型結果：

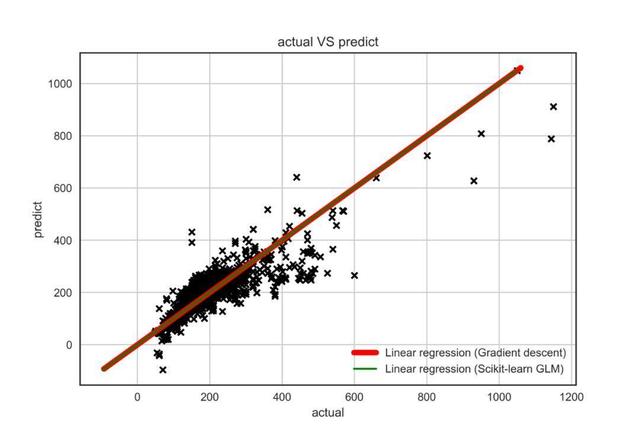
黑色標記是以真實值為橫坐標，預測值為縱坐標。綠色的線為用sklearn擬合的線性回歸模型，紅色的線為使用我們自己編寫的模型擬合的回歸線。我們發現，兩條線幾乎完全重合在一起，說明結論是一致的。

好了，如何不通過調包，一步步運用數學知識和代碼優勢還原線性回歸模型的方法就講到這里。如果，你完全讀懂了上述所有操作，那么我相信你已經入門了。

關于如何用python推導線性回歸模型的問題就講到這里，喜歡就點個關注吧~更多的 Python實戰教程也會繼續為大家更新！