您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
本文實例講述了Java完全二叉樹的創建與四種遍歷方法。分享給大家供大家參考,具體如下:
有如下的一顆完全二叉樹:
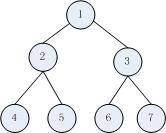
先序遍歷結果應該為:1 2 4 5 3 6 7
中序遍歷結果應該為:4 2 5 1 6 3 7
后序遍歷結果應該為:4 5 2 6 7 3 1
層序遍歷結果應該為:1 2 3 4 5 6 7
二叉樹的先序遍歷、中序遍歷、后序遍歷其實都是一樣的,都是執行遞歸操作。
我這記錄一下層次遍歷吧:層次遍歷需要用到隊列,先入隊在出隊,每次出隊的元素檢查是其是否有左右孩子,有則將其加入隊列,由于利用隊列的先進先出原理,進行層次遍歷。
下面記錄下完整代碼(java實現),包括幾種遍歷方法:
import java.util.ArrayDeque;
import java.util.ArrayList;
import java.util.List;
import java.util.Queue;
/**
* 定義二叉樹節點元素
* @author bubble
*
*/
class Node {
public Node leftchild;
public Node rightchild;
public int data;
public Node(int data) {
this.data = data;
}
}
public class TestBinTree {
/**
* 將一個arry數組構建成一個完全二叉樹
* @param arr 需要構建的數組
* @return 二叉樹的根節點
*/
public Node initBinTree(int[] arr) {
if(arr.length == 1) {
return new Node(arr[0]);
}
List<Node> nodeList = new ArrayList<>();
for(int i = 0; i < arr.length; i++) {
nodeList.add(new Node(arr[i]));
}
int temp = 0;
while(temp <= (arr.length - 2) / 2) { //注意這里,數組的下標是從零開始的
if(2 * temp + 1 < arr.length)
nodeList.get(temp).leftchild = nodeList.get(2 * temp + 1);
if(2 * temp + 2 < arr.length)
nodeList.get(temp).rightchild = nodeList.get(2 * temp + 2);
temp++;
}
return nodeList.get(0);
}
/**
* 層序遍歷二叉樹
* @param root 二叉樹根節點
* @param nodeQueue ,用到的隊列數據結構
*/
public void trivalBinTree(Node root, Queue<Node> nodeQueue) {
nodeQueue.add(root);
Node temp = null;
while ((temp = nodeQueue.poll()) != null) {
System.out.print(temp.data + " ");
if (temp.leftchild != null) {
nodeQueue.add(temp.leftchild);
}
if (temp.rightchild != null) {
nodeQueue.add(temp.rightchild);
}
}
}
/**
* 先序遍歷
* @param root 二叉樹根節點
*/
public void preTrival(Node root) {
if(root == null) {
return;
}
System.out.print(root.data + " ");
preTrival(root.leftchild);
preTrival(root.rightchild);
}
/**
* 中序遍歷
* @param root 二叉樹根節點
*/
public void midTrival(Node root) {
if(root == null) {
return;
}
midTrival(root.leftchild);
System.out.print(root.data + " ");
midTrival(root.rightchild);
}
/**
* 后序遍歷
* @param root 二叉樹根節點
*/
public void afterTrival(Node root) {
if(root == null) {
return;
}
afterTrival(root.leftchild);
afterTrival(root.rightchild);
System.out.print(root.data + " ");
}
public static void main(String[] args) {
TestBinTree btree = new TestBinTree();
int[] arr = new int[] {1,2,3,4,5,6,7};
Node root = btree.initBinTree(arr);
Queue<Node> nodeQueue = new ArrayDeque<>();
System.out.println("億速云測試結果:");
System.out.println("層序遍歷:");
btree.trivalBinTree(root, nodeQueue);
System.out.println("\n先序遍歷:");
btree.preTrival(root);
System.out.println("\n中序遍歷:");
btree.midTrival(root);
System.out.println("\n后序遍歷:");
btree.afterTrival(root);
}
}
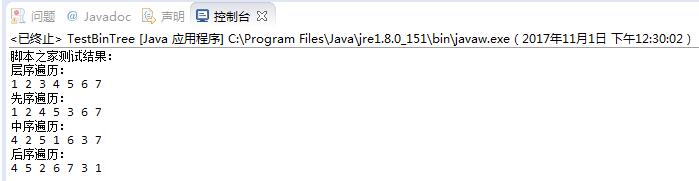
運行結果:
附:滿二叉樹 與完全二叉樹的區別
滿二叉樹是指這樣的一種二叉樹:除最后一層外,每一層上的所有結點都有兩個子結點。在滿二叉樹中,每一層上的結點數都達到最大值,即在滿二叉樹的第k層上有2k-1個結點,且深度為m的滿二叉樹有2m-1個結點。
完全二叉樹是指這樣的二叉樹:除最后一層外,每一層上的結點數均達到最大值;在最后一層上只缺少右邊的若干結點。
對于完全二叉樹來說,葉子結點只可能在層次最大的兩層上出現:對于任何一個結點,若其右分支下的子孫結點的最大層次為p,則其左分支下的子孫結點的最大層次或為p,或為p+1。
完全二叉樹具有以下兩個性質:
性質5:具有n個結點的完全二叉樹的深度為[log2n]+1。
性質6:設完全二叉樹共有n個結點。如果從根結點開始,按層次(每一層從左到右)用自然數1,2,……,n給結點進行編號,則對于編號為k(k=1,2,……,n)的結點有以下結論:
①若k=1,則該結點為根結點,它沒有父結點;若k>1,則該結點的父結點編號為INT(k/2)。
②若2k≤n,則編號為k的結點的左子結點編號為2k;否則該結點無左子結點(顯然也沒有右子結點)。
③若2k+1≤n,則編號為k的結點的右子結點編號為2k+1;否則該結點無右子結點。
滿二叉樹肯定是完全二叉樹,完全二叉樹不一定是滿二叉樹。
更多關于java算法相關內容感興趣的讀者可查看本站專題:《Java數據結構與算法教程》、《Java操作DOM節點技巧總結》、《Java文件與目錄操作技巧匯總》和《Java緩存操作技巧匯總》
希望本文所述對大家java程序設計有所幫助。
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。