Python語言描述隨機梯度下降法

1.梯度下降

1）什么是梯度下降？

因為梯度下降是一種思想，沒有嚴格的定義，所以用一個比喻來解釋什么是梯度下降。

簡單來說，梯度下降就是從山頂找一條最短的路走到山腳最低的地方。但是因為選擇方向的原因，我們找到的的最低點可能不是真正的最低點。如圖所示，黑線標注的路線所指的方向并不是真正的地方。

既然是選擇一個方向下山，那么這個方向怎么選？每次該怎么走？

先說選方向，在算法中是以隨機方式給出的，這也是造成有時候走不到真正最低點的原因。

如果選定了方向，以后每走一步，都是選擇最陡的方向，直到最低點。

總結起來就一句話：隨機選擇一個方向，然后每次邁步都選擇最陡的方向，直到這個方向上能達到的最低點。

2）梯度下降是用來做什么的?

在機器學習算法中,有時候需要對原始的模型構建損失函數,然后通過優化算法對損失函數進行優化，以便尋找到最優的參數，使得損失函數的值最小。而在求解機器學習參數的優化算法中，使用較多的就是基于梯度下降的優化算法(GradientDescent,GD)。

3）優缺點

優點：效率。在梯度下降法的求解過程中，只需求解損失函數的一階導數，計算的代價比較小，可以在很多大規模數據集上應用

缺點：求解的是局部最優值，即由于方向選擇的問題，得到的結果不一定是全局最優

步長選擇，過小使得函數收斂速度慢，過大又容易找不到最優解。

2.梯度下降的變形形式

根據處理的訓練數據的不同，主要有以下三種形式：

1）批量梯度下降法BGD(BatchGradientDescent):

針對的是整個數據集，通過對所有的樣本的計算來求解梯度的方向。

優點：全局最優解；易于并行實現；

缺點：當樣本數據很多時，計算量開銷大，計算速度慢

2）小批量梯度下降法MBGD（mini-batchGradientDescent）

把數據分為若干個批，按批來更新參數，這樣，一個批中的一組數據共同決定了本次梯度的方向，下降起來就不容易跑偏，減少了隨機性

優點：減少了計算的開銷量，降低了隨機性

3）隨機梯度下降法SGD（stochasticgradientdescent）

每個數據都計算算一下損失函數，然后求梯度更新參數。

優點：計算速度快

缺點：收斂性能不好

總結：SGD可以看作是MBGD的一個特例，及batch_size=1的情況。在深度學習及機器學習中，基本上都是使用的MBGD算法。

3.隨機梯度下降

隨機梯度下降（SGD）是一種簡單但非常有效的方法，多用用于支持向量機、邏輯回歸等凸損失函數下的線性分類器的學習。并且SGD已成功應用于文本分類和自然語言處理中經常遇到的大規模和稀疏機器學習問題。

SGD既可以用于分類計算，也可以用于回歸計算。

1）分類

a）核心函數

sklearn.linear_model.SGDClassifier

b）主要參數（詳細參數）

loss：指定損失函數。可選值：‘hinge'(默認),‘log',‘modified_huber',‘squared_hinge',‘perceptron',

"hinge":線性SVM

"log":邏輯回歸

"modified_huber":平滑損失，基于異常值容忍和概率估計

"squared_hinge":帶有二次懲罰的線性SVM

"perceptron":帶有線性損失的感知器

alpha:懲罰系數

c）示例代碼及詳細解釋

import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import SGDClassifier
from sklearn.datasets.samples_generator import make_blobs

##生產數據
X, Y = make_blobs(n_samples=50, centers=2, random_state=0, cluster_std=0.60)

##訓練數據
clf = SGDClassifier(loss="hinge", alpha=0.01)
clf.fit(X, Y)

## 繪圖
xx = np.linspace(-1, 5, 10)
yy = np.linspace(-1, 5, 10)

##生成二維矩陣
X1, X2 = np.meshgrid(xx, yy)
##生產一個與X1相同形狀的矩陣
Z = np.empty(X1.shape)
##np.ndenumerate 返回矩陣中每個數的值及其索引
for (i, j), val in np.ndenumerate(X1):
  x1 = val
  x2 = X2[i, j]
  p = clf.decision_function([[x1, x2]]) ##樣本到超平面的距離
  Z[i, j] = p[0]
levels = [-1.0, 0.0, 1.0]
linestyles = ['dashed', 'solid', 'dashed']
colors = 'k'
##繪制等高線：Z分別等于levels
plt.contour(X1, X2, Z, levels, colors=colors, linestyles=linestyles)
##畫數據點
plt.scatter(X[:, 0], X[:, 1], c=Y, cmap=plt.cm.Paired,
      edgecolor='black', s=20)
plt.axis('tight')
plt.show()

d）結果圖

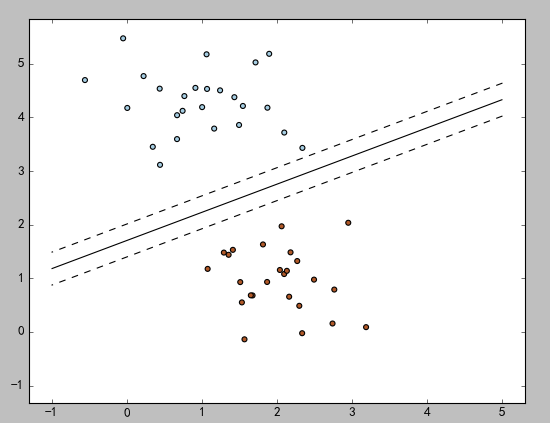
2）回歸

SGDRegressor非常適合回歸問題具有大量訓練樣本（>10000），對于其他的問題，建議使用的Ridge，Lasso或ElasticNet。

a）核心函數

sklearn.linear_model.SGDRegressor

b）主要參數（詳細參數）

loss：指定損失函數。可選值‘squared_loss'（默認）,‘huber',‘epsilon_insensitive',‘squared_epsilon_insensitive'

說明：此參數的翻譯不是特別準確，請參考官方文檔。

"squared_loss":采用普通最小二乘法

"huber":使用改進的普通最小二乘法，修正異常值

"epsilon_insensitive":忽略小于epsilon的錯誤

"squared_epsilon_insensitive":

alpha:懲罰系數

c）示例代碼

因為使用方式與其他線性回歸方式類似，所以這里只舉個簡單的例子：

import numpy as np
from sklearn import linear_model
n_samples, n_features = 10, 5
np.random.seed(0)
y = np.random.randn(n_samples)
X = np.random.randn(n_samples, n_features)
clf = linear_model.SGDRegressor()
clf.fit(X, y)

總結

以上就是本文關于Python語言描述隨機梯度下降法的全部內容，希望對大家有所幫助。感興趣的朋友可以繼續參閱本站其他相關專題，如有不足之處，歡迎留言指出。感謝朋友們對本站的支持！