您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
這篇文章主要介紹Python如何實現FM算法,文中介紹的非常詳細,具有一定的參考價值,感興趣的小伙伴們一定要看完!
1. 什么是FM?
FM即Factor Machine,因子分解機。
2. 為什么需要FM?
1、特征組合是許多機器學習建模過程中遇到的問題,如果對特征直接建模,很有可能會忽略掉特征與特征之間的關聯信息,因此,可以通過構建新的交叉特征這一特征組合方式提高模型的效果。
2、高維的稀疏矩陣是實際工程中常見的問題,并直接會導致計算量過大,特征權值更新緩慢。試想一個10000*100的表,每一列都有8種元素,經過one-hot獨熱編碼之后,會產生一個10000*800的表。因此表中每行元素只有100個值為1,700個值為0。
而FM的優勢就在于對這兩方面問題的處理。首先是特征組合,通過對兩兩特征組合,引入交叉項特征,提高模型得分;其次是高維災難,通過引入隱向量(對參數矩陣進行矩陣分解),完成對特征的參數估計。
3. FM用在哪?
我們已經知道了FM可以解決特征組合以及高維稀疏矩陣問題,而實際業務場景中,電商、豆瓣等推薦系統的場景是使用最廣的領域,打個比方,小王只在豆瓣上瀏覽過20部電影,而豆瓣上面有20000部電影,如果構建一個基于小王的電影矩陣,毫無疑問,里面將有199980個元素全為0。而類似于這樣的問題就可以通過FM來解決。
4. FM長什么樣?
在展示FM算法前,我們先回顧一下最常見的線性表達式:

其中w0為初始權值,或者理解為偏置項,wi為每個特征xi對應的權值。可以看到,這種線性表達式只描述了每個特征與輸出的關系。
FM的表達式如下,可觀察到,只是在線性表達式后面加入了新的交叉項特征及對應的權值。

5. FM交叉項的展開
5.1 尋找交叉項
FM表達式的求解核心在于對交叉項的求解。下面是很多人用來求解交叉項的展開式,對于第一次接觸FM算法的人來說可能會有疑惑,不知道公式怎么展開的,接下來筆者會手動推導一遍。

設有3個變量(特征)x1 x2 x3,每一個特征的隱變量分別為v1=(1 2 3)、v2=(4 5 6)、v3=(1 2 1),即:

設交叉項所組成的權矩陣W為對稱矩陣,之所以設為對稱矩陣是因為對稱矩陣有可以用向量乘以向量轉置替代的性質。
那么W=VVT,即

所以:

實際上,我們應該考慮的交叉項應該是排除自身組合的項,即對于x1x1、x2x2、x3x3不認為是交叉項,那么真正的交叉項為x1x2、x1x3、x2x1、x2x3、x3x1、x3x2。
去重后,交叉項即x1x2、x1x3、x2x3。這也是公式中1/2出現的原因。
5.2 交叉項權值轉換
對交叉項有了基本了解后,下面將進行公式的分解,還是以n=3為例,

所以:

wij可記作 或
或 ,這取決于vi是1*3 還是3*1 向量。
,這取決于vi是1*3 還是3*1 向量。
5.3 交叉項展開式
上面的例子是對3個特征做的交叉項推導,因此對具有n個特征,FM的交叉項公式就可推廣為:

我們還可以進一步分解:

所以FM算法的交叉項最終可展開為:

5.4隱向量v就是embedding vector?
假設訓練數據集dataMatrix的shape為(20000,9),取其中一行數據作為一條樣本i,那么樣本i 的shape為(1,9),同時假設隱向量vi的shape為(9,8)(注:8為自定義值,代表embedding vector的長度)
所以5.3小節中的交叉項可以表示為:
sum((inter_1)^2 - (inter_2)^2)/2
其中:
inter_1 =i*v shape為(1,8) inter_2 =np.multiply(i)*np.multiply(v) shape為(1,8)
可以看到,樣本i 經過交叉項中的計算后,得到向量shape為(1,8)的inter_1和inter_2。
由于維度變低,所以此計算過程可以近似認為在交叉項中對樣本i 進行了embedding vector轉換。
故,我們需要對之前的理解進行修正:
我們口中的隱向量vi實際上是一個向量組,其形狀為(輸入特征One-hot后的長度,自定義長度);
隱向量vi代表的并不是embedding vector,而是在對輸入進行embedding vector的向量組,也可理解為是一個權矩陣;
由輸入i*vi得到的向量才是真正的embedding vector。
具體可以結合第7節點的代碼實現進行理解。
6. 權值求解
利用梯度下降法,通過求損失函數對特征(輸入項)的導數計算出梯度,從而更新權值。設m為樣本個數,θ為權值。
如果是回歸問題,損失函數一般是均方誤差(MSE):

所以回歸問題的損失函數對權值的梯度(導數)為:

如果是二分類問題,損失函數一般是logit loss:

其中,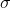

所以分類問題的損失函數對權值的梯度(導數)為:


相應的,對于常數項、一次項、交叉項的導數分別為:

7. FM算法的Python實現
FM算法的Python實現流程圖如下:

我們需要注意以下四點:
1. 初始化參數,包括對偏置項權值w0、一次項權值w以及交叉項輔助向量的初始化;
2. 定義FM算法;
3. 損失函數梯度的定義;
4. 利用梯度下降更新參數。
下面的代碼片段是以上四點的描述,其中的loss并不是二分類的損失loss,而是分類loss的梯度中的一部分:
loss = self.sigmoid(classLabels[x] * p[0, 0]) -1
實際上,二分類的損失loss的梯度可以表示為:
gradient = (self.sigmoid(classLabels[x] * p[0, 0]) -1)*classLabels[x]*p_derivative
其中 p_derivative 代表常數項、一次項、交叉項的導數(詳見本文第6小節)。
FM算法代碼片段
# 初始化參數
w = zeros((n, 1)) # 其中n是特征的個數
w_0 = 0.
v = normalvariate(0, 0.2) * ones((n, k))
for it in range(self.iter): # 迭代次數
# 對每一個樣本,優化
for x in range(m):
# 這邊注意一個數學知識:對應點積的地方通常會有sum,對應位置積的地方通常都沒有,詳細參見矩陣運算規則,本處計算邏輯在:http://blog.csdn.net/google19890102/article/details/45532745
# xi·vi,xi與vi的矩陣點積
inter_1 = dataMatrix[x] * v
# xi與xi的對應位置乘積 與 xi^2與vi^2對應位置的乘積 的點積
inter_2 = multiply(dataMatrix[x], dataMatrix[x]) * multiply(v, v) # multiply對應元素相乘
# 完成交叉項,xi*vi*xi*vi - xi^2*vi^2
interaction = sum(multiply(inter_1, inter_1) - inter_2) / 2.
# 計算預測的輸出
p = w_0 + dataMatrix[x] * w + interaction
print('classLabels[x]:',classLabels[x])
print('預測的輸出p:', p)
# 計算sigmoid(y*pred_y)-1準確的說不是loss,原作者這邊理解的有問題,只是作為更新w的中間參數,這邊算出來的是越大越好,而下面卻用了梯度下降而不是梯度上升的算法在
loss = self.sigmoid(classLabels[x] * p[0, 0]) - 1
if loss >= -1:
loss_res = '正方向 '
else:
loss_res = '反方向'
# 更新參數
w_0 = w_0 - self.alpha * loss * classLabels[x]
for i in range(n):
if dataMatrix[x, i] != 0:
w[i, 0] = w[i, 0] - self.alpha * loss * classLabels[x] * dataMatrix[x, i]
for j in range(k):
v[i, j] = v[i, j] - self.alpha * loss * classLabels[x] * (
dataMatrix[x, i] * inter_1[0, j] - v[i, j] * dataMatrix[x, i] * dataMatrix[x, i])FM算法完整實現
# -*- coding: utf-8 -*-
from __future__ import division
from math import exp
from numpy import *
from random import normalvariate # 正態分布
from sklearn import preprocessing
import numpy as np
'''
data : 數據的路徑
feature_potenital : 潛在分解維度數
alpha : 學習速率
iter : 迭代次數
_w,_w_0,_v : 拆分子矩陣的weight
with_col : 是否帶有columns_name
first_col : 首列有價值的feature的index
'''
class fm(object):
def __init__(self):
self.data = None
self.feature_potential = None
self.alpha = None
self.iter = None
self._w = None
self._w_0 = None
self.v = None
self.with_col = None
self.first_col = None
def min_max(self, data):
self.data = data
min_max_scaler = preprocessing.MinMaxScaler()
return min_max_scaler.fit_transform(self.data)
def loadDataSet(self, data, with_col=True, first_col=2):
# 我就是閑的蛋疼,明明pd.read_table()可以直接度,非要搞這樣的,顯得代碼很長,小數據下完全可以直接讀嘛,唉~
self.first_col = first_col
dataMat = []
labelMat = []
fr = open(data)
self.with_col = with_col
if self.with_col:
N = 0
for line in fr.readlines():
# N=1時干掉列表名
if N > 0:
currLine = line.strip().split()
lineArr = []
featureNum = len(currLine)
for i in range(self.first_col, featureNum):
lineArr.append(float(currLine[i]))
dataMat.append(lineArr)
labelMat.append(float(currLine[1]) * 2 - 1)
N = N + 1
else:
for line in fr.readlines():
currLine = line.strip().split()
lineArr = []
featureNum = len(currLine)
for i in range(2, featureNum):
lineArr.append(float(currLine[i]))
dataMat.append(lineArr)
labelMat.append(float(currLine[1]) * 2 - 1)
return mat(self.min_max(dataMat)), labelMat
def sigmoid(self, inx):
# return 1.0/(1+exp(min(max(-inx,-10),10)))
return 1.0 / (1 + exp(-inx))
# 得到對應的特征weight的矩陣
def fit(self, data, feature_potential=8, alpha=0.01, iter=100):
# alpha是學習速率
self.alpha = alpha
self.feature_potential = feature_potential
self.iter = iter
# dataMatrix用的是mat, classLabels是列表
dataMatrix, classLabels = self.loadDataSet(data)
print('dataMatrix:',dataMatrix.shape)
print('classLabels:',classLabels)
k = self.feature_potential
m, n = shape(dataMatrix)
# 初始化參數
w = zeros((n, 1)) # 其中n是特征的個數
w_0 = 0.
v = normalvariate(0, 0.2) * ones((n, k))
for it in range(self.iter): # 迭代次數
# 對每一個樣本,優化
for x in range(m):
# 這邊注意一個數學知識:對應點積的地方通常會有sum,對應位置積的地方通常都沒有,詳細參見矩陣運算規則,本處計算邏輯在:http://blog.csdn.net/google19890102/article/details/45532745
# xi·vi,xi與vi的矩陣點積
inter_1 = dataMatrix[x] * v
# xi與xi的對應位置乘積 與 xi^2與vi^2對應位置的乘積 的點積
inter_2 = multiply(dataMatrix[x], dataMatrix[x]) * multiply(v, v) # multiply對應元素相乘
# 完成交叉項,xi*vi*xi*vi - xi^2*vi^2
interaction = sum(multiply(inter_1, inter_1) - inter_2) / 2.
# 計算預測的輸出
p = w_0 + dataMatrix[x] * w + interaction
print('classLabels[x]:',classLabels[x])
print('預測的輸出p:', p)
# 計算sigmoid(y*pred_y)-1
loss = self.sigmoid(classLabels[x] * p[0, 0]) - 1
if loss >= -1:
loss_res = '正方向 '
else:
loss_res = '反方向'
# 更新參數
w_0 = w_0 - self.alpha * loss * classLabels[x]
for i in range(n):
if dataMatrix[x, i] != 0:
w[i, 0] = w[i, 0] - self.alpha * loss * classLabels[x] * dataMatrix[x, i]
for j in range(k):
v[i, j] = v[i, j] - self.alpha * loss * classLabels[x] * (
dataMatrix[x, i] * inter_1[0, j] - v[i, j] * dataMatrix[x, i] * dataMatrix[x, i])
print('the no %s times, the loss arrach %s' % (it, loss_res))
self._w_0, self._w, self._v = w_0, w, v
def predict(self, X):
if (self._w_0 == None) or (self._w == None).any() or (self._v == None).any():
raise NotFittedError("Estimator not fitted, call `fit` first")
# 類型檢查
if isinstance(X, np.ndarray):
pass
else:
try:
X = np.array(X)
except:
raise TypeError("numpy.ndarray required for X")
w_0 = self._w_0
w = self._w
v = self._v
m, n = shape(X)
result = []
for x in range(m):
inter_1 = mat(X[x]) * v
inter_2 = mat(multiply(X[x], X[x])) * multiply(v, v) # multiply對應元素相乘
# 完成交叉項
interaction = sum(multiply(inter_1, inter_1) - inter_2) / 2.
p = w_0 + X[x] * w + interaction # 計算預測的輸出
pre = self.sigmoid(p[0, 0])
result.append(pre)
return result
def getAccuracy(self, data):
dataMatrix, classLabels = self.loadDataSet(data)
w_0 = self._w_0
w = self._w
v = self._v
m, n = shape(dataMatrix)
allItem = 0
error = 0
result = []
for x in range(m):
allItem += 1
inter_1 = dataMatrix[x] * v
inter_2 = multiply(dataMatrix[x], dataMatrix[x]) * multiply(v, v) # multiply對應元素相乘
# 完成交叉項
interaction = sum(multiply(inter_1, inter_1) - inter_2) / 2.
p = w_0 + dataMatrix[x] * w + interaction # 計算預測的輸出
pre = self.sigmoid(p[0, 0])
result.append(pre)
if pre < 0.5 and classLabels[x] == 1.0:
error += 1
elif pre >= 0.5 and classLabels[x] == -1.0:
error += 1
else:
continue
# print(result)
value = 1 - float(error) / allItem
return value
class NotFittedError(Exception):
"""
Exception class to raise if estimator is used before fitting
"""
pass
if __name__ == '__main__':
fm()以上是“Python如何實現FM算法”這篇文章的所有內容,感謝各位的閱讀!希望分享的內容對大家有幫助,更多相關知識,歡迎關注億速云行業資訊頻道!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。