js尾調用優化的實現

尾調用（Tail Call）是函數式編程的一個重要概念，本文介紹它的含義和用法。

一、什么是尾調用？

尾調用的概念非常簡單，一句話就能說清楚，就是指某個函數的最后一步是調用另一個函數。

function f(x){
 return g(x);
}

上面代碼中，函數f的最后一步是調用函數g，這就叫尾調用。

以下兩種情況，都不屬于尾調用。

// 情況一
function f(x){
 let y = g(x);
 return y;
}

// 情況二
function f(x){
 return g(x) + 1;
}

上面代碼中，情況一是調用函數g之后，還有別的操作，所以不屬于尾調用，即使語義完全一樣。情況二也屬于調用后還有操作，即使寫在一行內。

尾調用不一定出現在函數尾部，只要是最后一步操作即可。

function f(x) {
 if (x > 0) {
  return m(x)
 }
 return n(x);
}

上面代碼中，函數m和n都屬于尾調用，因為它們都是函數f的最后一步操作。

二、尾調用優化

尾調用之所以與其他調用不同，就在于它的特殊的調用位置。

我們知道，函數調用會在內存形成一個"調用記錄"，又稱"調用幀"（call frame），保存調用位置和內部變量等信息。如果在函數A的內部調用函數B，那么在A的調用記錄上方，還會形成一個B的調用記錄。等到B運行結束，將結果返回到A，B的調用記錄才會消失。如果函數B內部還調用函數C，那就還有一個C的調用記錄棧，以此類推。所有的調用記錄，就形成一個"調用棧"（call stack）。

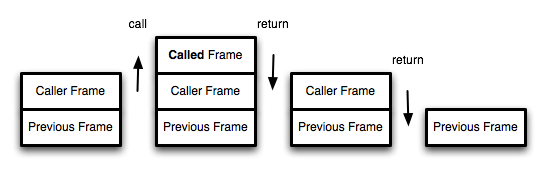
尾調用由于是函數的最后一步操作，所以不需要保留外層函數的調用記錄，因為調用位置、內部變量等信息都不會再用到了，只要直接用內層函數的調用記錄，取代外層函數的調用記錄就可以了。

function f() {
 let m = 1;
 let n = 2;
 return g(m + n);
}
f();

// 等同于
function f() {
 return g(3);
}
f();

// 等同于
g(3);

上面代碼中，如果函數g不是尾調用，函數f就需要保存內部變量m和n的值、g的調用位置等信息。但由于調用g之后，函數f就結束了，所以執行到最后一步，完全可以刪除 f() 的調用記錄，只保留 g(3) 的調用記錄。

這就叫做"尾調用優化"（Tail call optimization），即只保留內層函數的調用記錄。如果所有函數都是尾調用，那么完全可以做到每次執行時，調用記錄只有一項，這將大大節省內存。這就是"尾調用優化"的意義。

三、尾遞歸

函數調用自身，稱為遞歸。如果尾調用自身，就稱為尾遞歸。

遞歸非常耗費內存，因為需要同時保存成千上百個調用記錄，很容易發生"棧溢出"錯誤（stack overflow）。但對于尾遞歸來說，由于只存在一個調用記錄，所以永遠不會發生"棧溢出"錯誤。

function factorial(n) {
 if (n === 1) return 1;
 return n * factorial(n - 1);
}

factorial(5) // 120

上面代碼是一個階乘函數，計算n的階乘，最多需要保存n個調用記錄，復雜度 O(n) 。

如果改寫成尾遞歸，只保留一個調用記錄，復雜度 O(1) 。

function factorial(n, total) {
 if (n === 1) return total;
 return factorial(n - 1, n * total);
}

factorial(5, 1) // 120

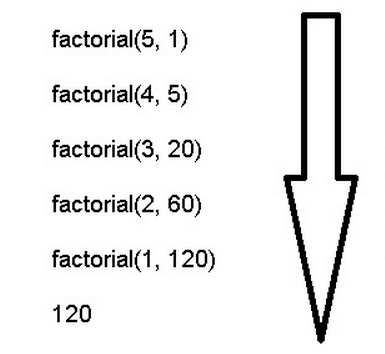
由此可見，"尾調用優化"對遞歸操作意義重大，所以一些函數式編程語言將其寫入了語言規格。ES6也是如此，第一次明確規定，所有 ECMAScript 的實現，都必須部署"尾調用優化"。這就是說，在 ES6 中，只要使用尾遞歸，就不會發生棧溢出，相對節省內存。

四、遞歸函數的改寫

尾遞歸的實現，往往需要改寫遞歸函數，確保最后一步只調用自身。做到這一點的方法，就是把所有用到的內部變量改寫成函數的參數。比如上面的例子，階乘函數 factorial 需要用到一個中間變量 total ，那就把這個中間變量改寫成函數的參數。這樣做的缺點就是不太直觀，第一眼很難看出來，為什么計算5的階乘，需要傳入兩個參數5和1？

兩個方法可以解決這個問題。方法一是在尾遞歸函數之外，再提供一個正常形式的函數。

function tailFactorial(n, total) {
 if (n === 1) return total;
 return tailFactorial(n - 1, n * total);
}

function factorial(n) {
 return tailFactorial(n, 1);
}

factorial(5) // 120

上面代碼通過一個正常形式的階乘函數 factorial ，調用尾遞歸函數 tailFactorial ，看起來就正常多了。

函數式編程有一個概念，叫做柯里化（currying），意思是將多參數的函數轉換成單參數的形式。這里也可以使用柯里化。

function currying(fn, n) {
 return function (m) {
  return fn.call(this, m, n);
 };
}

function tailFactorial(n, total) {
 if (n === 1) return total;
 return tailFactorial(n - 1, n * total);
}

const factorial = currying(tailFactorial, 1);

factorial(5) // 120

上面代碼通過柯里化，將尾遞歸函數 tailFactorial 變為只接受1個參數的 factorial 。

第二種方法就簡單多了，就是采用ES6的函數默認值。

function factorial(n, total = 1) {
 if (n === 1) return total;
 return factorial(n - 1, n * total);
}

factorial(5) // 120

上面代碼中，參數 total 有默認值1，所以調用時不用提供這個值。

總結一下，遞歸本質上是一種循環操作。純粹的函數式編程語言沒有循環操作命令，所有的循環都用遞歸實現，這就是為什么尾遞歸對這些語言極其重要。對于其他支持"尾調用優化"的語言（比如Lua，ES6），只需要知道循環可以用遞歸代替，而一旦使用遞歸，就最好使用尾遞歸。

（[說明] 本文摘自我寫的《ECMAScript 6入門》）

五、嚴格模式

ES6的尾調用優化只在嚴格模式下開啟，正常模式是無效的。

這是因為在正常模式下，函數內部有兩個變量，可以跟蹤函數的調用棧。

• arguments：返回調用時函數的參數。
• func.caller：返回調用當前函數的那個函數。

尾調用優化發生時，函數的調用棧會改寫，因此上面兩個變量就會失真。嚴格模式禁用這兩個變量，所以尾調用模式僅在嚴格模式下生效。

以上就是本文的全部內容，希望對大家的學習有所幫助，也希望大家多多支持億速云。