溫馨提示×
您好,登錄后才能下訂單哦!
點擊 登錄注冊 即表示同意《億速云用戶服務條款》
您好,登錄后才能下訂單哦!
這篇文章主要介紹python怎么實現beta分布概率密度函數的方法,文中介紹的非常詳細,具有一定的參考價值,感興趣的小伙伴們一定要看完!
如下所示:
beta分布的最大特點是其多樣性, 從下圖可以看出, beta分布具有各種形態, 有U形, 類似正態分布的形狀, 類似uniform分布的形狀等, 正式這一特質使beta分布在共軛先驗的計算中起到重要作用:
import matplotlib.pyplot as plt
import numpy as np
from scipy import stats
from matplotlib import style
style.use('ggplot')
params = [0.5, 1, 2, 3]
x = np.linspace(0, 1, 100)
f, ax = plt.subplots(len(params), len(params), sharex=True, sharey=True)
for i in range(4):
for j in range(4):
alpha = params[i]
beta = params[j]
pdf = stats.beta(alpha, beta).pdf(x)
ax[i, j].plot(x, pdf)
ax[i, j].plot(0, 0, label='alpha={:3.2f}\nbeta={:3.2f}'.format(alpha, beta), alpha=0)
plt.setp(ax[i, j], xticks=[0.0, 0.2, 0.4, 0.6, 0.8, 1.0], yticks=[0,2,4,6,8,10])
ax[i, j].legend(fontsize=10)
ax[3, 0].set_xlabel('theta', fontsize=16)
ax[0, 0].set_ylabel('pdf(theta)', fontsize=16)
plt.suptitle('Beta PDF', fontsize=16)
plt.tight_layout()
plt.show()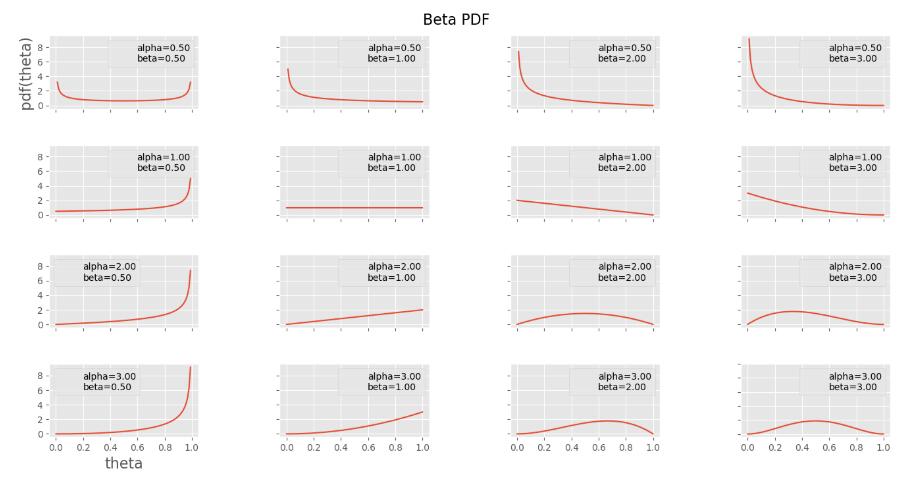
以上是“python怎么實現beta分布概率密度函數的方法”這篇文章的所有內容,感謝各位的閱讀!希望分享的內容對大家有幫助,更多相關知識,歡迎關注億速云行業資訊頻道!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。