溫馨提示×
您好，登錄后才能下訂單哦！
點擊 登錄注冊 即表示同意《億速云用戶服務條款》
您好，登錄后才能下訂單哦！
數據歸一化問題是數據挖掘中特征向量表達時的重要問題，當不同的特征成列在一起的時候，由于特征本身表達方式的原因而導致在絕對數值上的小數據被大數據“吃掉”的情況，這個時候我們需要做的就是對抽取出來的features vector進行歸一化處理，以保證每個特征被分類器平等對待。下面我描述幾種常見的Normalization Method，并提供相應的python實現（其實很簡單）：
1、(0,1)標準化：
這是最簡單也是最容易想到的方法，通過遍歷feature vector里的每一個數據，將Max和Min的記錄下來，并通過Max-Min作為基數（即Min=0，Max=1）進行數據的歸一化處理：
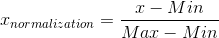
LaTex：{x}_{normalization}=\frac{x-Min}{Max-Min}
Python實現：
def MaxMinNormalization(x,Max,Min): x = (x - Min) / (Max - Min); return x;
找大小的方法直接用np.max()和np.min()就行了，盡量不要用python內建的max()和min()，除非你喜歡用List管理數字。
2、Z-score標準化：
這種方法給予原始數據的均值（mean）和標準差（standard deviation）進行數據的標準化。經過處理的數據符合標準正態分布，即均值為0，標準差為1，這里的關鍵在于復合標準正態分布，個人認為在一定程度上改變了特征的分布，關于使用經驗上歡迎討論，我對這種標準化不是非常地熟悉，轉化函數為：
LaTex：{x}_{normalization}=\frac{x-\mu }{\sigma }
Python實現：
def Z_ScoreNormalization(x,mu,sigma): x = (x - mu) / sigma; return x;
這里一樣，mu（即均值）用np.average()，sigma（即標準差）用np.std()即可。
3、Sigmoid函數
Sigmoid函數是一個具有S形曲線的函數，是良好的閾值函數，在(0, 0.5)處中心對稱，在(0, 0.5)附近有比較大的斜率，而當數據趨向于正無窮和負無窮的時候，映射出來的值就會無限趨向于1和0，是個人非常喜歡的“歸一化方法”，之所以打引號是因為我覺得Sigmoid函數在閾值分割上也有很不錯的表現，根據公式的改變，就可以改變分割閾值，這里作為歸一化方法，我們只考慮(0, 0.5)作為分割閾值的點的情況：
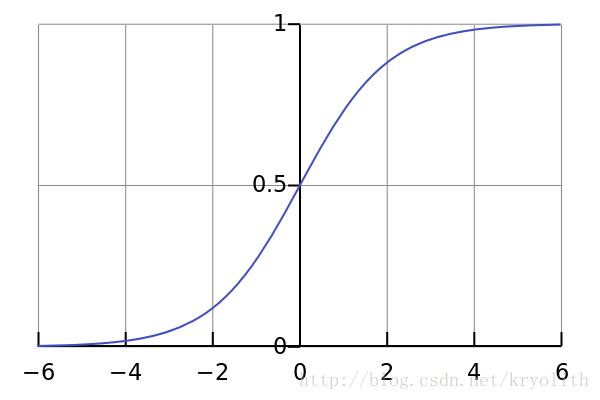
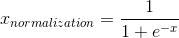
LaTex：{x}_{normalization}=\frac{1}{1+{e}^{-x}}
Python實現：
def sigmoid(X,useStatus): if useStatus: return 1.0 / (1 + np.exp(-float(X))); else: return float(X);
這里useStatus管理是否使用sigmoid的狀態，方便調試使用。
以上就是本文的全部內容，希望對大家的學習有所幫助，也希望大家多多支持億速云。
免責聲明：本站發布的內容（圖片、視頻和文字）以原創、轉載和分享為主，文章觀點不代表本網站立場，如果涉及侵權請聯系站長郵箱：is@yisu.com進行舉報，并提供相關證據，一經查實，將立刻刪除涉嫌侵權內容。
