您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
克里金法時一種用于空間插值的地學統計方法。
克里金法用半變異測定空間要素,要素即自相關要素。
半變異公式為:
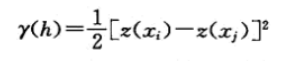
其中γ(h) 是已知點 xi 和 xj 的半變異,***h***表示這兩個點之間的距離,z是屬性值。
假設不存在漂移,普通克里金法重點考慮空間相關因素,并用擬合的半變異直接進行插值。
估算某測量點z值的通用方程為:
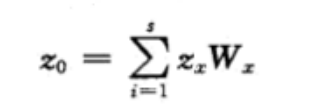
式中,z0是待估計值,zx是已知點x的值,Wx是每個已知點關聯的權重,s是用于估計的已知點數目。
權重可以由一組矩陣方程得到。
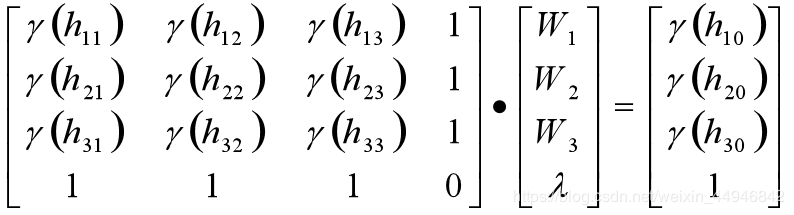
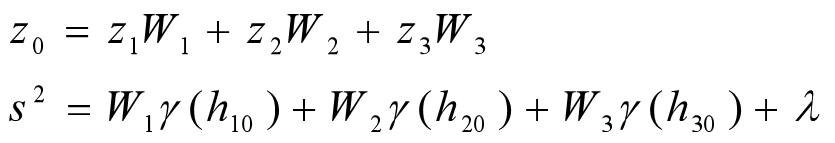
此程序對半變異進行擬合時采用的時最簡單的正比例函數擬合
數據為csv格式
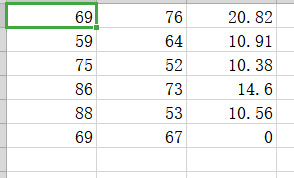
保存格式如下:
第一行為第一個點以此類推
最后一行是待求點坐標,其中z為未知值,暫且假設為0
代碼如下:
import numpy as np
from math import*
from numpy.linalg import *
h_data=np.loadtxt(open('高程點數據.csv'),delimiter=",",skiprows=0)
print('原始數據如下(x,y,z):\n未知點高程初值設為0\n',h_data)
def dis(p1,p2):
a=pow((pow((p1[0]-p2[0]),2)+pow((p1[1]-p2[1]),2)),0.5)
return a
def rh(z1,z2):
r=1/2*pow((z1[2]-z2[2]),2)
return r
def proportional(x,y):
xx,xy=0,0
for i in range(len(x)):
xx+=pow(x[i],2)
xy+=x[i]*y[i]
k=xy/xx
return k
r=[];pp=[];p=[];
for i in range(len(h_data)):
pp.append(h_data[i])
for i in range(len(pp)):
for j in range(len(pp)):
p.append(dis(pp[i],pp[j]))
r.append(rh(pp[i],pp[j]))
r=np.array(r).reshape(len(h_data),len(h_data))
r=np.delete(r,len(h_data)-1,axis =0)
r=np.delete(r,len(h_data)-1,axis =1)
h=np.array(p).reshape(len(h_data),len(h_data))
h=np.delete(h,len(h_data)-1,axis =0)
oh=h[:,len(h_data)-1]
h=np.delete(h,len(h_data)-1,axis =1)
hh=np.triu(h,0)
rr=np.triu(r,0)
r0=[];h0=[];
for i in range(len(h_data)-1):
for j in range(len(h_data)-1):
if hh[i][j] !=0:
a=h[i][j]
h0.append(a)
if rr[i][j] !=0:
a=rr[i][j]
r0.append(a)
k=proportional(h0,r0)
hnew=h*k
a2=np.ones((1,len(h_data)-1))
a1=np.ones((len(h_data)-1,1))
a1=np.r_[a1,[[0]]]
hnew=np.r_[hnew,a2]
hnew=np.c_[hnew,a1]
print('半方差聯立矩陣:\n',hnew)
oh=np.array(k*oh)
oh=np.r_[oh,[1]]
w=np.dot(inv(hnew),oh)
print('權陣運算結果:\n',w)
z0,s2=0,0
for i in range(len(h_data)-1):
z0=w[i]*h_data[i][2]+z0
s2=w[i]*oh[i]+s2
s2=s2+w[len(h_data)-1]
print('未知點高程值為:\n',z0)
print('半變異值為:\n',pow(s2,0.5))
input()
運算結果
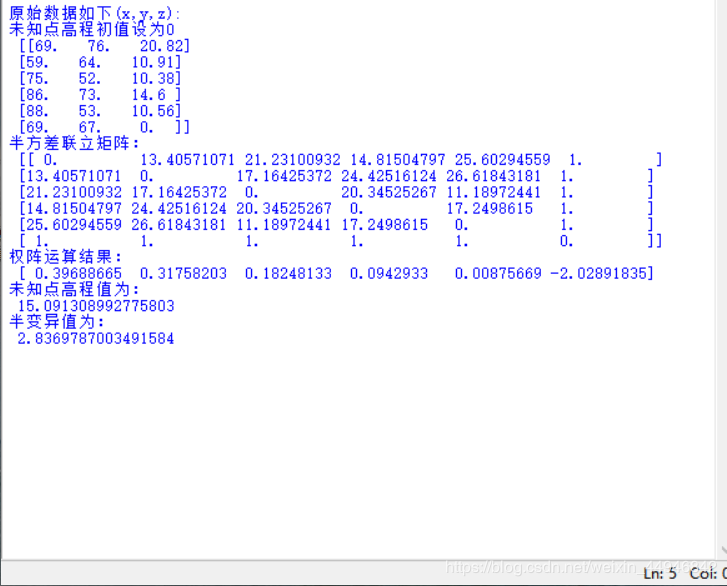
python初學,為了完成作業寫了個小程序來幫助計算,因為初學知識有限,有很多地方寫的很復雜,可以優化的地方很多。 還望讀者諒解,歡迎斧正謝謝!
參考文獻:
【1】(美)張康聰 著;陳健飛等譯. 地理信息系統導論(第三版). 北京:清華大學出版社, 2009.04.
以上就是本文的全部內容,希望對大家的學習有所幫助,也希望大家多多支持億速云。
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。