使用python如何實現DFT

這篇文章給大家分享的是有關使用python如何實現DFT的內容。小編覺得挺實用的，因此分享給大家做個參考，一起跟隨小編過來看看吧。

DFT

DFT(Discrete Fourier Transform)，離散傅里葉變化，可以將離散信號變換到頻域，它的公式非常簡單:

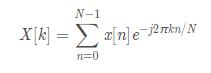
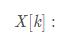離散頻率下標為k時的頻率大小

離散時域信號序列

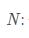信號序列的長度，也就是采樣的個數

如果你剛接觸DFT，并且之前沒有信號處理的相關經驗，那么第一次看到這個公式，你可能有一些疑惑，為什么這個公式就能進行時域與頻域之間的轉換呢？

這里，我不打算去解釋它，因為我水平有限，說的不清楚。相反，在這里我想介紹，作為一個程序員，如何如實現DFT

從矩陣的角度看DFT

DFT的公式，雖然簡單，但是理解起來比較麻煩，我發現如果用矩陣相乘的角度來理解上面的公式，就會非常簡單，直接上矩陣：

OK，通過上面的表示，我們很容易將DFT理解成為一種矩陣相乘的操作，這對于我們編碼是很容易的。

Talk is cheap, show me the code

根據上面的理解，我們只需要構建出S SS矩陣，然后做矩陣相乘，就等得到DFT的結果

在這之前，我們先介紹如何生成正弦信號，以及如何用scipy中的fft模塊進行DFT操作，以驗證我們的結果是否正確

正弦信號

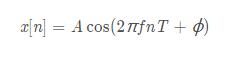
A: 幅度

f: 信號頻率

n: 時間下標

T: 采樣間隔, 等于 1/fs，fs為采樣頻率

? \phi?: 相位

下面介紹如何生成正弦信號

import numpy as np
import matplotlib.pyplot as plt

%matplotlib inline

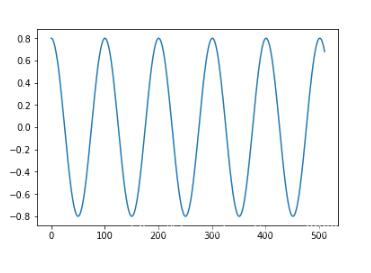
def generate_sinusoid(N, A, f0, fs, phi):
 '''
 N(int) : number of samples
 A(float) : amplitude
 f0(float): frequency in Hz
 fs(float): sample rate
 phi(float): initial phase
 
 return 
 x (numpy array): sinusoid signal which lenght is M
 '''
 
 T = 1/fs
 n = np.arange(N) # [0,1,..., N-1]
 x = A * np.cos( 2*f0*np.pi*n*T + phi )
 
 return x

N = 511
A = 0.8
f0 = 440
fs = 44100
phi = 0

x = generate_sinusoid(N, A, f0, fs, phi)

plt.plot(x)
plt.show()

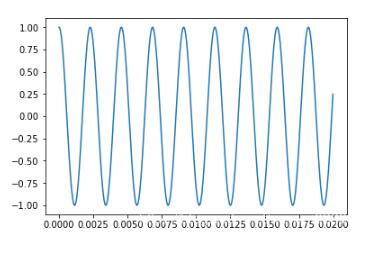
# 另一種生成正弦信號的方法，生成時長為t的序列
def generate_sinusoid_2(t, A, f0, fs, phi):
 '''
 t (float) : 生成序列的時長
 A (float) : amplitude
 f0 (float) : frequency
 fs (float) : sample rate
 phi(float) : initial phase
 
 returns
 x (numpy array): sinusoid signal sequence
 '''
 
 T = 1.0/fs
 N = t / T
 
 return generate_sinusoid(N, A, f0, fs, phi)

A = 1.0
f0 = 440
fs = 44100
phi = 0
t = 0.02

x = generate_sinusoid_2(t, A, f0, fs, phi)

n = np.arange(0, 0.02, 1/fs)
plt.plot(n, x)

Scipy FFT

介紹如何Scipy的FFT模塊計算DFT

注意，理論上輸入信號的長度必須是才能做FFT，而scipy中FFT卻沒有這樣的限制

這是因為當長度不等于時，scipy fft默認做DFT

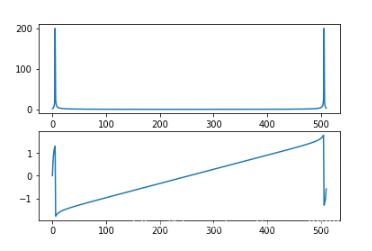
from scipy.fftpack import fft

# generate sinusoid
N = 511
A = 0.8
f0 = 440
fs = 44100
phi = 1.0
x = generate_sinusoid(N, A, f0, fs, phi)

# fft is
X = fft(x)
mX = np.abs(X) # magnitude
pX = np.angle(X) # phase

# plot the magnitude and phase
plt.subplot(2,1,1)
plt.plot(mX)

plt.subplot(2,1,2)
plt.plot(pX)
plt.show()

自己實現DFT

自己實現DFT的關鍵就是構造出S，有兩種方式：

def generate_complex_sinusoid(k, N):
 '''
 k (int): frequency index
 N (int): length of complex sinusoid in samples
 
 returns
 c_sin (numpy array): the generated complex sinusoid (length N)
 '''
 
 n = np.arange(N)
 
 c_sin = np.exp(1j * 2 * np.pi * k * n / N)
 
 return np.conjugate(c_sin)

def generate_complex_sinusoid_matrix(N):
 '''
 N (int): length of complex sinusoid in samples
 
 returns
 c_sin_matrix (numpy array): the generated complex sinusoid (length N)
 '''
 
 n = np.arange(N)
 n = np.expand_dims(n, axis=1)  # 擴充維度，將1D向量，轉為2D矩陣，方便后面的矩陣相乘
 
 k = n
 
 m = n.T * k / N     # [N,1] * [1, N] = [N,N]
 
 S = np.exp(1j * 2 * np.pi * m)  # 計算矩陣 S
 
 return np.conjugate(S)

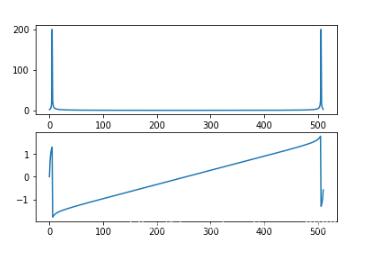
# 生成信號，用于測試
N = 511
A = 0.8
f0 = 440
fs = 44100
phi = 1.0
x = generate_sinusoid(N, A, f0, fs, phi)

# 第一種方式計算DFT
X_1 = np.array([])
for k in range(N):
 s = generate_complex_sinusoid(k, N)
 X_1 = np.append(X_1, np.sum(x * s))
 
mX = np.abs(X_1)
pX = np.angle(X_1)

# plot the magnitude and phase
plt.subplot(2,1,1)
plt.plot(mX)

plt.subplot(2,1,2)
plt.plot(pX)
plt.show()

# 結果和scipy的結果基本相同

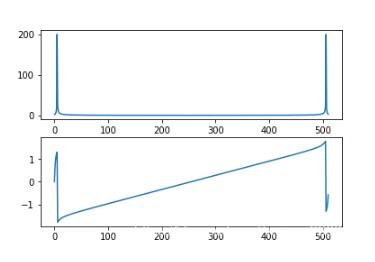
# 第二種方法計算DFT
S = generate_complex_sinusoid_matrix(N)
X_2 = np.dot(S, x)

mX = np.abs(X_2)
pX = np.angle(X_2)

# plot the magnitude and phase
plt.subplot(2,1,1)
plt.plot(mX)

plt.subplot(2,1,2)
plt.plot(pX)
plt.show()

感謝各位的閱讀！關于“使用python如何實現DFT”這篇文章就分享到這里了，希望以上內容可以對大家有一定的幫助，讓大家可以學到更多知識，如果覺得文章不錯，可以把它分享出去讓更多的人看到吧！