您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
在一般問題的優化中,最速下降法和共軛梯度法都是非常有用的經典方法,但最速下降法往往以”之”字形下降,速度較慢,不能很快的達到最優值,共軛梯度法則優于最速下降法,在前面的某個文章中,我們給出了牛頓法和最速下降法的比較,牛頓法需要初值點在最優點附近,條件較為苛刻。
算法來源:《數值最優化方法》高立,P111
我們選用了64維的二次函數來作為驗證函數,具體參見上書111頁。
采用的三種方法為:
共軛梯度方法(FR格式)、共軛梯度法(PRP格式)、最速下降法
# -*- coding: utf-8 -*-
"""
Created on Sat Oct 01 15:01:54 2016
@author: zhangweiguo
"""
import sympy,numpy
import math
import matplotlib.pyplot as pl
from mpl_toolkits.mplot3d import Axes3D as ax3
import SD#這個文件里有最速下降法SD的方法,參見前面的博客
#共軛梯度法FR、PRP兩種格式
def CG_FR(x0,N,E,f,f_d):
X=x0;Y=[];Y_d=[];
n = 1
ee = f_d(x0)
e=(ee[0]**2+ee[1]**2)**0.5
d=-f_d(x0)
Y.append(f(x0)[0,0]);Y_d.append(e)
a=sympy.Symbol('a',real=True)
print '第%2s次迭代:e=%f' % (n, e)
while n<N and e>E:
n=n+1
g1=f_d(x0)
f1=f(x0+a*f_d(x0))
a0=sympy.solve(sympy.diff(f1[0,0],a,1))
x0=x0-d*a0
X=numpy.c_[X,x0];Y.append(f(x0)[0,0])
ee = f_d(x0)
e = math.pow(math.pow(ee[0,0],2)+math.pow(ee[1,0],2),0.5)
Y_d.append(e)
g2=f_d(x0)
beta=(numpy.dot(g2.T,g2))/numpy.dot(g1.T,g1)
d=-f_d(x0)+beta*d
print '第%2s次迭代:e=%f'%(n,e)
return X,Y,Y_d
def CG_PRP(x0,N,E,f,f_d):
X=x0;Y=[];Y_d=[];
n = 1
ee = f_d(x0)
e=(ee[0]**2+ee[1]**2)**0.5
d=-f_d(x0)
Y.append(f(x0)[0,0]);Y_d.append(e)
a=sympy.Symbol('a',real=True)
print '第%2s次迭代:e=%f' % (n, e)
while n<N and e>E:
n=n+1
g1=f_d(x0)
f1=f(x0+a*f_d(x0))
a0=sympy.solve(sympy.diff(f1[0,0],a,1))
x0=x0-d*a0
X=numpy.c_[X,x0];Y.append(f(x0)[0,0])
ee = f_d(x0)
e = math.pow(math.pow(ee[0,0],2)+math.pow(ee[1,0],2),0.5)
Y_d.append(e)
g2=f_d(x0)
beta=(numpy.dot(g2.T,g2-g1))/numpy.dot(g1.T,g1)
d=-f_d(x0)+beta*d
print '第%2s次迭代:e=%f'%(n,e)
return X,Y,Y_d
if __name__=='__main__':
'''
G=numpy.array([[21.0,4.0],[4.0,15.0]])
#G=numpy.array([[21.0,4.0],[4.0,1.0]])
b=numpy.array([[2.0],[3.0]])
c=10.0
x0=numpy.array([[-10.0],[100.0]])
'''
m=4
T=6*numpy.eye(m)
T[0,1]=-1;T[m-1,m-2]=-1
for i in xrange(1,m-1):
T[i,i+1]=-1
T[i,i-1]=-1
W=numpy.zeros((m**2,m**2))
W[0:m,0:m]=T
W[m**2-m:m**2,m**2-m:m**2]=T
W[0:m,m:2*m]=-numpy.eye(m)
W[m**2-m:m**2,m**2-2*m:m**2-m]=-numpy.eye(m)
for i in xrange(1,m-1):
W[i*m:(i+1)*m,i*m:(i+1)*m]=T
W[i*m:(i+1)*m,i*m+m:(i+1)*m+m]=-numpy.eye(m)
W[i*m:(i+1)*m,i*m-m:(i+1)*m-m]=-numpy.eye(m)
mm=m**2
mmm=m**3
G=numpy.zeros((mmm,mmm))
G[0:mm,0:mm]=W;G[mmm-mm:mmm,mmm-mm:mmm]=W;
G[0:mm,mm:2*mm]=-numpy.eye(mm)
G[mmm-mm:mmm,mmm-2*mm:mmm-mm]=-numpy.eye(mm)
for i in xrange(1,m-1):
G[i*mm:(i+1)*mm,i*mm:(i+1)*mm]=W
G[i*mm:(i+1)*mm,i*mm-mm:(i+1)*mm-mm]=-numpy.eye(mm)
G[i*mm:(i+1)*mm,i*mm+mm:(i+1)*mm+mm]=-numpy.eye(mm)
x_goal=numpy.ones((mmm,1))
b=-numpy.dot(G,x_goal)
c=0
f = lambda x: 0.5 * (numpy.dot(numpy.dot(x.T, G), x)) + numpy.dot(b.T, x) + c
f_d = lambda x: numpy.dot(G, x) + b
x0=x_goal+numpy.random.rand(mmm,1)*100
N=100
E=10**(-6)
print '共軛梯度PR'
X1, Y1, Y_d1=CG_FR(x0,N,E,f,f_d)
print '共軛梯度PBR'
X2, Y2, Y_d2=CG_PRP(x0,N,E,f,f_d)
figure1=pl.figure('trend')
n1=len(Y1)
n2=len(Y2)
x1=numpy.arange(1,n1+1)
x2=numpy.arange(1,n2+1)
X3, Y3, Y_d3=SD.SD(x0,N,E,f,f_d)
n3=len(Y3)
x3=range(1,n3+1)
pl.semilogy(x3,Y3,'g*',markersize=10,label='SD:'+str(n3))
pl.semilogy(x1,Y1,'r*',markersize=10,label='CG-FR:'+str(n1))
pl.semilogy(x2,Y2,'b*',markersize=10,label='CG-PRP:'+str(n2))
pl.legend()
#圖像顯示了三種不同的方法各自迭代的次數與最優值變化情況,共軛梯度方法是明顯優于最速下降法的
pl.xlabel('n')
pl.ylabel('f(x)')
pl.show()
最優值變化趨勢:
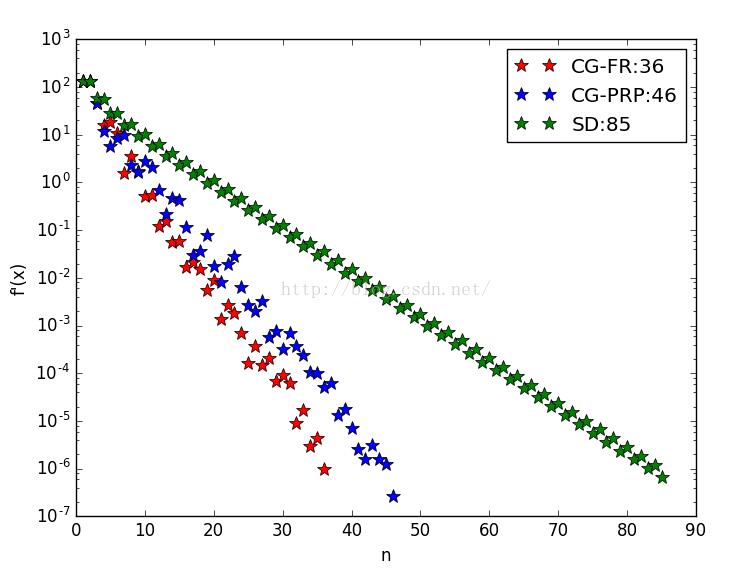
從圖中可以看出,最速下降法SD的迭代次數是最多的,在與共軛梯度(FR與PRP兩種方法)的比較中,明顯較差。
補充知識:python實現牛頓迭代法和二分法求平方根,精確到小數點后無限多位-4
首先來看一下牛頓迭代法求平方根的過程:計算3的平方根

如圖,是求根號3的牛頓迭代法過程。這里使用的初始迭代值(也就是猜測值)為1,其實可以為任何值最終都能得到結果。每次開始,先檢測猜測值是否合理,不合理時,用上面的平均值來換掉猜測值,依次繼續迭代,直到猜測值合理。
原理:現在取一個猜測值 a, 如果猜測值合理的話,那么就有a^2=x,即x/a=a ,x為被開方數。不合理的話呢,就用表中的猜測值和商的平均值來換掉猜測值。當不合理時,比如 a>真實值,那么x/a<真實值,這時候取a 與 x/a 的平均值來代替a的話,那么新的a就會比原來的a要更接近真實值。同理有 a<真實值 的情況。于是,這樣不斷迭代下去最終是一個a不斷收斂到真實值的一個過程。于是不斷迭代就能得到真實值,證明了迭代法是正確的。
附上我的python代碼:
利用python整數運算,python整數可以無限大,可以實現小數點后無限多位
#二分法求x的平方根小數點下任意K位數的精準值,利用整數運算 #思想:利用二分法,每次乘以10,取中間值,比較大小,從而定位精確值的范圍,將根擴大10倍,則被開方數擴大100倍。 #quotient(商)牛頓迭代法:先猜測一個值,再求商,然后用猜測值和商的中間值代替猜測值,擴大倍數,繼續進行。
import math
from math import sqrt
def check_precision(l,h,p,len1):#檢查是否達到了精確位
l=str(l);h=str(h)
if len(l)<=len1+p or len(h)<=len1+p:
return False
for i in range(len1,p+len1):#檢查小數點后面的p個數是否相等
if l[i]!=h[i]: #當l和h某一位不相等時,說明沒有達到精確位
return False
return True
def print_result(x,len1,p):
x=str(x)
if len(x)-len1<p:#沒有達到要求的精度就已經找出根
s=x[:len1]+"."+x[len1:]+'0'*(p-len(x)+len1)
else:s=x[:len1]+"."+x[len1:len1+p]
print(s)
def binary_sqrt(x,p):
x0=int(sqrt(x))
if x0*x0==x: #完全平方數直接開方,不用繼續進行
print_result(x0,len(str(x0)),p)
return
len1=len(str(x0))#找出整數部分的長度
l=0;h=x
while(not check_precision(l,h,p,len1)):#沒有達到精確位,繼續循環
if not l==0:#第一次l=0,h=x時不用乘以10,直接取中間值
h=h*10 #l,h每次擴大10倍
l=l*10
x=x*100 #x每次要擴大100倍,因為平方
m=(l+h)//2
if m*m==x:
return print_result(m,len1,p)
elif m*m>x:
h=m
else:
l=m
return print_result(l,len1,p)#當達到了要求的精度,直接返回l
#牛頓迭代法求平方根
def newton_sqrt(x,p):
x0=int(sqrt(x))
if x0*x0==x: #完全平方數直接開方,不用繼續進行
print_result(x0,len(str(x0)),p)
return
len1=len(str(x0))#找出整數部分的長度
g=1;q=x//g;g=(g+q)//2
while(not check_precision(g,q,p,len1)):
x=x*100
g=g*10
q=x//g #求商
g=(g+q)//2 #更新猜測值為猜測值和商的中間值
return print_result(g,len1,p)
while True:
x=int(input("請輸入待開方數:"))
p=int(input("請輸入精度:"))
print("binary_sqrt:",end="")
binary_sqrt(x,p)
print("newton_sqrt:",end="")
newton_sqrt(x,p)
以上這篇基于Python共軛梯度法與最速下降法之間的對比就是小編分享給大家的全部內容了,希望能給大家一個參考,也希望大家多多支持億速云。
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。